17

Лекция №3 Непараметрическое (независящее от распределения) обучение дискриминантных функций

3.1. Пространство весов

Мы уже обсуждали тот факт, что вектор образа X представляется как точка в пространстве образов и что пространство может быть разбито на подобласти для образов, принадлежащих различным категориям. Решающая поверхность, которая делит пространство может быть линейной, кусочно-линейной или нелинейной и может быть в общем виде представлена как:

где и

представляют собой образ и весовой вектор. Проблема обучения системы состоит в том, чтобы найти вектор W, показанный на рис.3.1 на основе априорной информации, полученной от обучающей выборки. Возможно и даже более удобно исследовать поведение обучающих алгоритмов в пространстве весов. Пространство весов есть (n+1) - размерности Эвклидова пространства, в котором координаты ₁ ₂ ... _n+1. Для каждого прототипа , k=1,2,...,M, m=1,2,...,N_k (где M представляет число категорий и N_k представляет собой число прототипов, принадлежащих к категории K, в пространстве W (пространство весов) имеется гиперплоскость, в которой

любой весовой вектор W на положительной стороне гиперплоскости дает w^Тz.. 0. Т.е., если прототип принадлежит категории ₁, любой весовой вектор W на этой стороне гиперплоскости будет вероятно классифицировать . Аналогичные аргументы могут быть рассмотрены для любого весового вектора на другой стороне гиперплоскости, где w^Тz.. 0.

Возьмем 2-х классовую проблему для иллюстрации. Предположим, что мы имеем последовательность N₁ образов, принадлежащих ₁ с общим числом образов N = N₁ + N_l. Предположим также, что ₁ и ₂ -два линейно разделяемых класса. Тогда может быть найден вектор  , такой,что:

и

где . и представляют собой категории ₁ и ₂ соответственно.

В общем, для N образов имеется N гиперплоскостей в весовом пространстве. Область решения для категории ₁ в W - пространстве это область, которая лежит на положительной стороне N₁ гиперплоскостей для категории ₁ и на отрицательной для N₂ гиперплоскостей для категории ₂. Предположим, что мы имеем три прототипа Z¹, Z², Z³ и знаем, что все они принадлежат категории ₁ . Три гиперплоскости могут быть нарисованы в W - пространстве, как показано на Рис.3.1а, заштрихованная область на Рис.3.1а показывает решающие области в двухклассовой проблеме. В этой области

и

Т.е. любое в этом районе будет вероятно классифицировать прототипы Z¹, Z², Z³ как принадлежащие ₁ , в то время как поперечно заштрихованные области, показанные на рис.3в

d₁

d₂

но d₃ любой  из этой области будет классифицировать Z¹ и Z² как принадлежащий категории ₁ и классифицировать Z³ как относящийся к категории ₂ .

К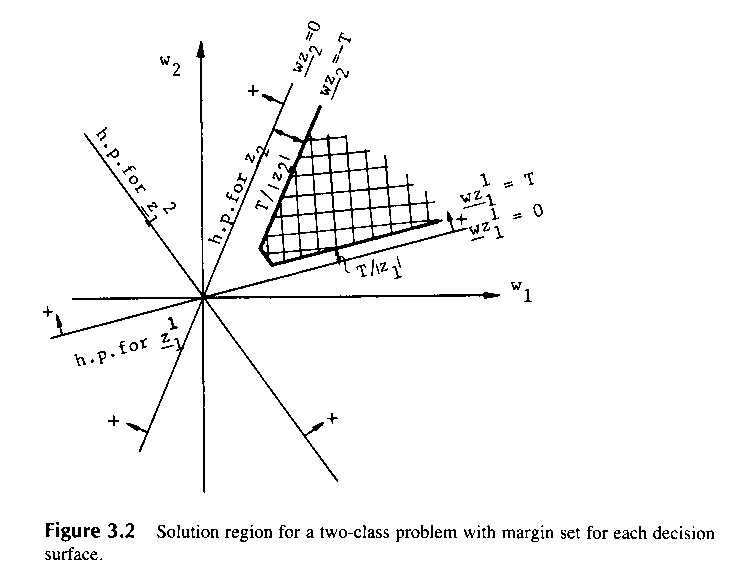 ак обсуждалось в части 2 решающая поверхность для двухклассовой задачи предполагает, что d(w,x) будет больше 0 для всех образов из одного класса и меньше 0 для образов, принадлежащих к другому классу. Но если все заменить на их отрицательные значения - , то решающая поверхность может быть обобщена как часть  пространства, в котором:

^Tz0 ₌ -

наша проблема становится в нахождении , которое обеспечивает положительность всех неравенств.

Иногда может быть желательно иметь ограничение (порог) в дискриминантной функции, такой что:

, (3.6)

где T0 ограничение (порог). Любой , удовлетворяющий неравенству (3.6) является весовым вектором решения. Решающая область теперь изменяется так, как показано на рис.3.2.

В заштрихованной области: оба и - положительные, в то время как отметим, что вдоль исходной гиперплоскости образа

, (3.7)

и что вектор Z (расширенный Z) является перпендикулярным к гиперплоскости и направлен в ее положительную сторону. Тогда линия отстоит от на расстояние . Доказательство этого оставим читателю.

3.2. Процедура обучения с коррекцией ошибок

Очевидно, что для случая двух классов ошибка может существовать, если

.

Тогда нам необходимо подвинуть весовой вектор в положительную сторону гиперплоскости для , другими словами передвигаем вектор W в область правильного решения. Наиболее прямой путь сделать это - передвинуть W в направлении перпендикулярном к гиперплоскости (т.е. в направлении от или -). Вообще коррекция W может быть сформулирована следующим образом:

заменить W(k) на W(k+1) , так что

, если

, если

, если классифицировано правильно,

где и - весовые вектора на k-ом и (k+1)-ом шагу коррекции, соответственно. Добавление корректирующего члена заставляет вектор двигаться в направлении . Аналогично, вычитание корректирующего члена передвигает вектор направлении -.

В течение этой обучающей процедуры образы представляются по одному, всего N=N₁ + N₂ прототипов (обучающих образов). После одной итерации все образы представляются снова в той же последовательности, чтобы получить новую итерацию.

Существует несколько правил выбора величины С:

- правило с фиксированной коррекцией,

- правило абсолютной коррекции,

- правило частичной коррекции.

3.2.1. Правило с фиксированной коррекцией

В этом алгоритме С - выбирается как фиксированная положительная константа. Этот алгоритм начинается с любого w(0) и выражение (3.10) применяется к обучающей последовательности P, P = .

В целом процесс настройки весов будет закончен за конечное число шагов. Выбор С для этого процесса не очень важен. Если теорема сходимости справедлива для С=1, то она будет справедлива для любого С 1, так как изменение С фактически масштабирует все образы без изменения их разделимости.

3.2.2. Правило абсолютной коррекции

В этом алгоритме С выбирается как наименьшее целое число, которое передвигает поперек гиперплоскости образа в область решения w каждый раз как классификатор делает ошибку. Пусть - среднее из векторов, которые не удовлетворяют неравенству w  z T . Константа С выбирается так, что

,

поэтому

Если Т=0, должно быть больше 0 или . Взяв абсолютную величину в (3.3) получаем

.

Правило абсолютной коррекции также дает решающий весовой вектор за конечное число шагов.

3.2.3. Правило с частичной коррекцией

В W пространстве расширенный вектор образа Z - перпендикулярен гиперплоскости и направлен в положительном направлении, как показано на рис.3.3.

Расстояние от до желаемой гиперплоскости будет:

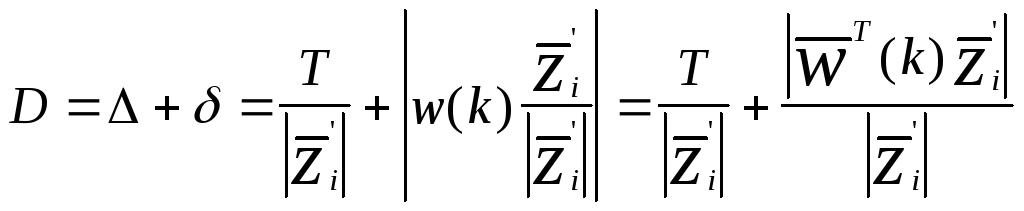(3.15)

Когда находится на другой стороне гиперплоскости

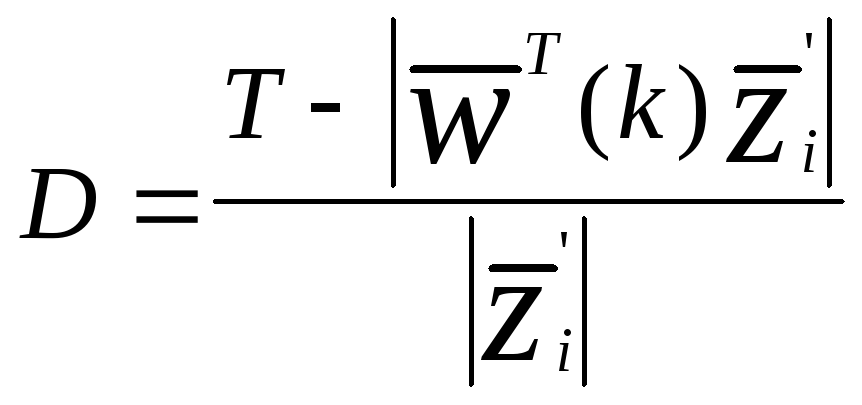
В алгоритме с частичной коррекцией С - выбрано так, что двигается на часть расстояния в направлении нормали к желаемой гиперплоскости. То есть

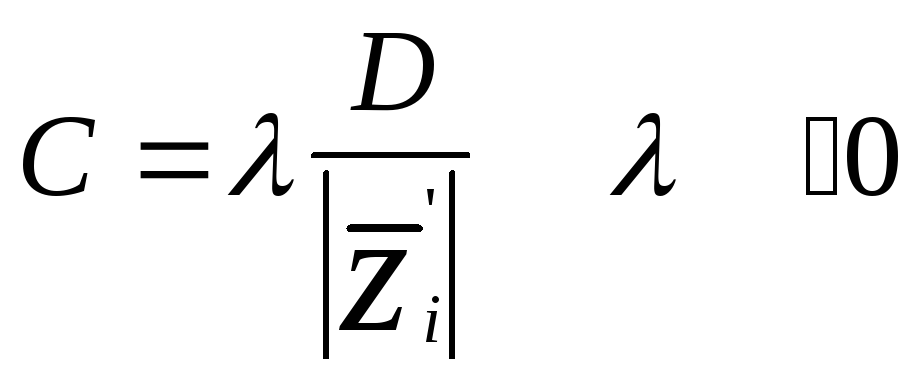
и

-=

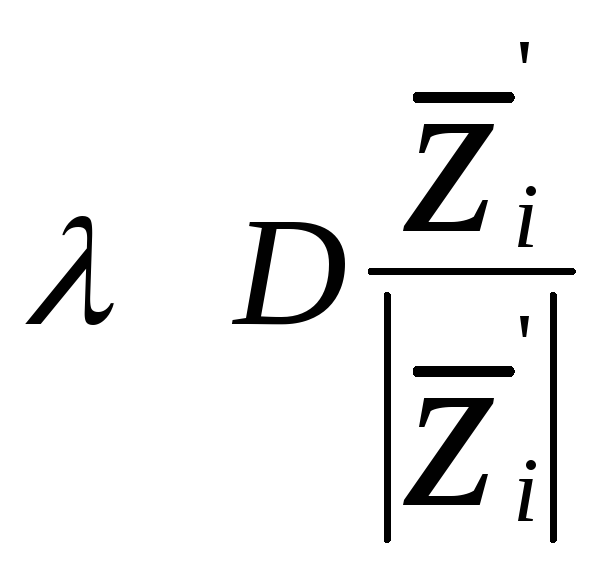
Если порог положить равным 0, то:

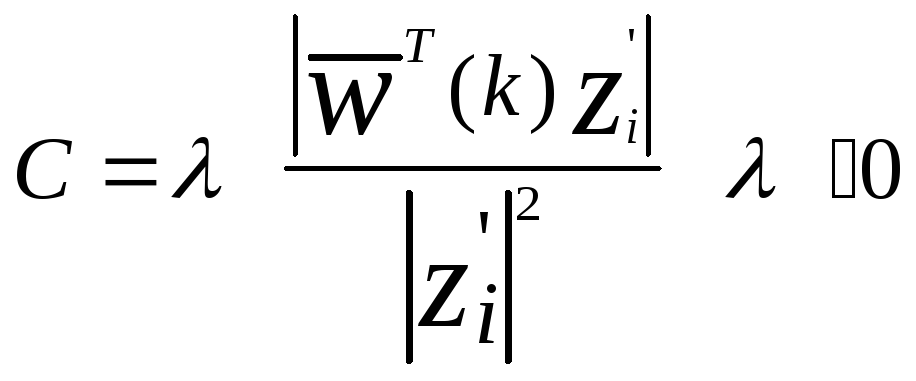
можно видеть, что когда =1 коррекция происходит до гиперплоскости (правило абсолютной коррекции) и когда 1 коррекция короче, чем до гиперплоскости (under relaxation), когда 1 коррекция больше чем до гиперплоскости, (over relaxation).

Для 02 правило частичной коррекции будет или заканчиваться на весовом векторе в конечное число шагов или сходиться к точке на границе решающего пространства весов.

Процедура обучения для всех перечисленных 3-х алгоритмов выглядит следующим образом:

1) Взять любой из обучающей последовательности и проверить d(z), для определения класса (предполагается М=2).

2) Если получен правильный ответ, переходим к следующему

3) Если имеет место ошибочная классификация, изменяем w(k) на w(k+1).

4) После того, как будут проверены все из обучающей последовательности, повторяем все процедуры заново в том же порядке. Если линейно разделимы , все три алгоритма будут сходиться к правильному .

На рис 3.4. показаны шаги коррекции для трех различных алогритмов. Абсолютная коррекция заканчивается за 3 шага, в то время как частичная за 4 шага.

Рис 3.4.

Для количества классов больше 2 (M2) может быть предложена подобная процедура. Предположим, что мы имеем обучающую последовательность для всех образов классов w_i i=1,2,...,M.

Вычислим дискриминантные функции

d_i()=, i=1,2,...,M

Очевидно, мы желаем:

d_i()d_j() 

3.3. Градиентные методы

3.3.1. Общий метод градиентного спуска

Метод градиентного спуска является другим приближением к обучающим системам. Градиентный вектор обладает важным свойством указывающий максимальную скорость увеличения функции по мере увеличения аргумента. Процедура настройки весов может быть сформулирована как:

= (3.25)

где J(w) - критерий качества, который минимизируется настройкой . Минимум J(w) может быть достигнут передвижением в направлении отрицательного градиента. Процедура может быть описана следующим образом:

1. Начать с некоторого произвольно выбранного вектора w(1) и вычислить градиентный вектор

2. Получаем следующую величину w(2) передвигаясь на некоторое расстояние от w(1) в направлении наиболее крутого спуска.

_k в уравнении (3.25) - положительный скалярный множитель, который устанавливает размер шага. Для его оптимального выбора предполагаем, что J(w) может быть аппоксимирован как:

(3.26)

где

подставляя (3.25) в (3.26) получим:

(3.27)

Полагая

для минимизации мы получим

(3.28)

или

, (3.29)

которое эквивалентно алгоритму Ньютона для оптимального спуска, в котором

_k = D ^-1.

Некоторые проблемы могут возникнуть с этим оптимальным _k ; D ^-1 в (3.29) может не существовать; используемые матричные операции требуют значительных временных затрат; предположение поверхности второго порядка может быть некорректным. Исходя из этих соображений лучшим выходом будет положить _k равным константе.

3.3.2. Персептронная функция критерия

Пусть функция критерия будет:

 (3.31)

где суммирование осуществляется по неправильно классифицированным векторам образов. Геометрически J_p(w) пропорционально сумме расстояний неправильно классифицированных образов от гиперплоскости.

Возьмем производную от J_p(w) по w(k) :

 (3.32)

где w(k) означает величину w на k-ой итерации. Персептронный обучающий алгоритм может быть сформулирован как

w(k+1) = w(k) - (3.33)

w(k+1) = w(k) + _k  (3.34)

где Р - последовательность неправильно классифицированных образов при данном w(k) . Уравнение (3.34) может быть затем интерпретировано в том смысле, что (k+1) весовой вектор может быть получен добавлением умноженной на некоторый множитель сумму неправильно классифицированных образов для

k-ого весового вектора.

Это процедура, называемая "many-at-time" ("большое время"), т.к. мы определяем w^Tz для всех zР, только после того как все образы были классифицированы.

Если мы делаем настройку после каждого неправильно классифицированного образа (мы называем это "one-at-a-time") процедура функция критерия становится

J(w) = -w^Tz (3.35)

и

J(w) = -z

Алгоритм обучения будет иметь вид

w(k+1) = w(k) +_kz (3.37)

Это правило с фиксированным инкрементом, если _k = с (константа).

3.3.3. Релаксационная функция критерия

Функкция критерия, используемая в этом алгоритме, имеет вид

(3.38)

Р - здесь снова последовательность неправильно классифицированных образов при заданном w. То есть Р состоит из тех z , для которых -w^Tz +b0

или: w^Tz  b. Градиент J_r(w) по w(k) дает

(3.39)

Базовый релаксационный обучающий алгоритм формулируется как

(3.40)

Э то также "many-at-time" алгоритм. Соответствующий "one-at-a-time" алгоритм будет:

(3.41)

который становится алгоритмом частичной коррекции с  = _k .

3.4. Обучение кусочно-линейных машин

В общем случае не существует теорем сходимости для для обучающих процедур коммитет или других кусочно-линейных машин. Одна процедура, которая часто бывает удовлетворительной приводится ниже. Пусть М=2 и имеется R дискриминантных функций, где R - нечетное. Тогда

(3.42)

Классификация в коммитет-машине будет затем выполняться согласно

(3.43)

т ак что

(3.44)

г де:

(3.45)

Отметим, что так как R - нечетное, d(z) не может быть равно 0 и будет всегда нечетным. Так как d(z) равно разнице между числом d_i(z) 0 и d_i(z)  0 для весового вектора w_i (k) для k-ой итерации. В нашем случае мы всегда желаем иметь d_i(z) 0 . Другими словами мы желаем иметь больше весовых векторов, которые дают d_i(z) 0 .

Когда d_i(z)  0, имеет место неправильная классификация. Будет очевидным, что в этом случае будет [ R+d(z) ] / 2 весовых векторов среди w_i (k), i=1,2,...,R, которые дают отрицательные ответы [d_i(z)  0] и [ R-d(z) ] / 2 весовых векторов , которые дают положительные ответы [d_i(z) 0]. Для получения правильной классификации нам необходимо изменить, по крайней мере n ответов w_i (k) от -1 к +1, где n может быть найдено из уравнения:

(3.46)

В первых скобках представлено число d_i , которое сейчас больше нуля, выражение в скобках после минуса представляет число d_i , которое меньше нуля. Минимальная величина n тогда будет

n_min = [d(z) + 1] / 2 , (3.47)

которое дает минимальное число векторов, необходимых для настройки.

Процедура для настройки весового вектора:

1) убираем наименьший отрицательный d_i(z) среди отрицательных d_i(z) ;

2) настраиваем [d(z) + 1] / 2 весовых векторов по следующему правилу:

w_i (k+1) = w_i (k) + сz, (3.48)

таким образом, что из результирующие d_i(z) становятся положительными. Все другие весовые векторы остаются неизменными на этой стадии;

3) если на k-ой стадии машина неправильно классифицирует образ, принадлежащий w₂ , делаем классифицирующие коэффициенты с отрицательной величиной, так что

w_i (k+1) = w_i (k) - сz.

3.5. Практические соображения, касающиеся метода обучения с коррекцией ошибок

Поскольку правила коррекции ошибок никогда не допускают ошибки при классификации шаблонов без коррекции дискриминантной функции, некоторые выборки могут сказаться. Например, для случая двух нормально распределенных классов с перекрытием всегда будет присутствовать ошибка, даже при выборе оптимума в одном из классов. Правило коррекции ошибок будет влиять на оптимум постоянно, он будет меняться и никогда не стабилизируется.

Для случая, когда классы имеют больше чем один «кластер» или «группировок» в шаблонной области, метод обучения с коррекцией ошибок снова сталкивается с проблемами. Решение состоит в добавлении правила остановки. Но это правило остановки должно быть применено соответствующее, иначе система может завершить работу с «бедным» w. Другой метод решения таких проблем состоит в использовании процедур обучения, не являющимися коррекцией ошибок, таких как кластеризация (определение только способов многорежимных проблем), стохастическая аппроксимация, функции потенциалов или процедура нахождения минимума квадратичной ошибки.

3.6. Процедуры минимума квадратичной ошибки

3.6.1. Минимум квадратичной ошибки и псевдоынверсный метод

Допустим, что мы желаем получить равенства

Zw = b (3.50)

вместо неравенств zw>0. В таком случае нам нужно решить линейных уравнений, где N – общее число прототипов для всех классов, N_i – число прототипов для класса _i, а M – общее число классов. Тогда z и b могут быть определены так:

( 3.51) и

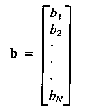
(3.52)

Если матрица Z квадратная и не сингулярная, то мы можем сказать:

w = Z^-1b (3.53)

и решить это уравнение для неизвестного w. Но в основном Z – прямоугольная (то есть строк больше, чем столбцов), то есть существует много решения системы Zw=b. Определим вектор ошибок как

и функцию квадратичного критерия как

Возьмем частную производную от J_s по w_s, наблюдаем:

и ли в матричной форме

У становка J_s(w) = 0 дает

и ли

w = Z^#b (3.59)

где Z^# = (Z^TZ)^-1Z^T называется псевдоынверсной или обобщенной инверсной матрицей Z. У Z^# есть следующие свойства: (1) Z^#Z = 1, однако, обычно ZZ^#  1 и (2) Z^# = Z^-1 если Z – квадратная и несингулярная. Значение b в равенстве (3.52) может быть установлено произвольно, учитывая лишь то, что b_i > i. Если нет другой информации, хорошим выбором является:

b = [1 1 1 …. 1 ] = u^T

На самом деле, если b = u^T, то решение минимальной квадратичной ошибки приближается к аппроксимации минимума средней квадратичной ошибки Байесовской дискриминантной функции. Заметим, что данный метод не является коррекцией ошибки, так как здесь не вычисляется новое w для каждого z. На самом деле, все z связаны вместе и нужно только одно решение; таким образом, время обучения очень мало.

3.6.2. Метод Хо-Кашьпа

Когда функциональный критерий J(w) нужно минимизировать не только по w, но и по b (то есть предположить, что b не константа), обучение производится по алгоритму, называемому методом Хо-Кашьпа. Используется тот же функциональный критерий J(w), что и в урванении (3.55), который приведен и ниже:

Ч астные производные от J(w) по w и b приведены ниже:

и

У становка дJ/дw = 0 дает

w = (Z^TZ)^-1Z^Tb = Z^#b (3.63)

Так как все компоненты b по определению должны быть положительными, установка b может производиться так:

b(k+1) = b(k) + b(k) (3.64)

где

г де символами k, i и c представляются итерационный индекс, индекс компоненты вектора и положительный корректирующий инкремент соответственно. Из равенства (3.63) имеем:

w(k+1) = Z^# b(k+1) (3.66)

Объединяя равенства (3.63), (3.64), (3.66), мы получаем:

w(k+1) = w(k) + Z^#b(k) (3.67)

Вспоминая, что все компоненты вектора b(k) = (b₁, b₂, … b_N)^T положительны, получаем:

w(1) = Z^#b(1), b(1)>0 (3.68)

e(k) = Zw(k) – b(k) (3.69)

алгоритм для нахождения весов и выбора b может быть представлен в следующей форме: