1. Интегралы вида

Для нахождения таких интегралов используют следующие приемы.

2.7.1.1 Если хотя бы одно из чисел и – нечетное целое положительное число, например, , то делают подстановку , тогда . Выражение под знаком интеграла преобразуют так:

В итоге получается

то есть получен интеграл от степенной функции.

Пример 24. Найти интеграл .

Решение.

2. Если 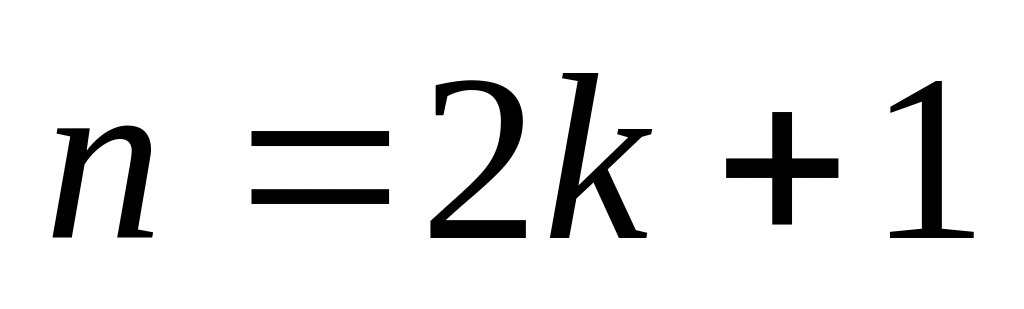, то делают подстановку , тогда . Выражение под знаком интеграла преобразуют анало-гично предыдущему случаю:

Пример 25. Найти интеграл .

Решение.

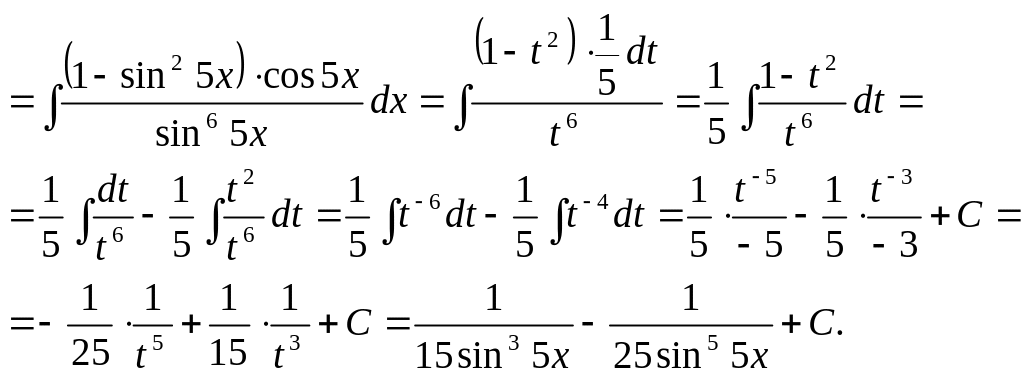
2.7.1.3 Если , – целые неотрицательные четные числа, то в этом случае используют формулы понижения степени

, , .

Пример 26. Найти интеграл .

Решение.

в первом интеграле у функции степень четная, используем формулу понижения степени . Во втором интеграле используем метод подведения под знак дифференциала:

2.7.1.4 Если – четное отрицательное целое число, тогда используют подстановку , а . При данной подста-новке

, , , .

В некоторых случаях удобнее сделать подстановку

, .

Пример 27. Найти интеграл .

Решение.

– четное отрицатель-ное целое число. Используем подстановку

.

2.7.2 Интегралы вида и , где , – рациональные функции

В первом случае делают подстановку , . Во втором – , а , тогда .

Пример 28. Найти интеграл .

Решение.

, тогда

2.7.3 Интегралы вида

Здесь – рациональная функция от синуса и коси-нуса. Для нахождения данного интеграла используют универсальную тригонометрическую подстановку: , тогда ,

, , .

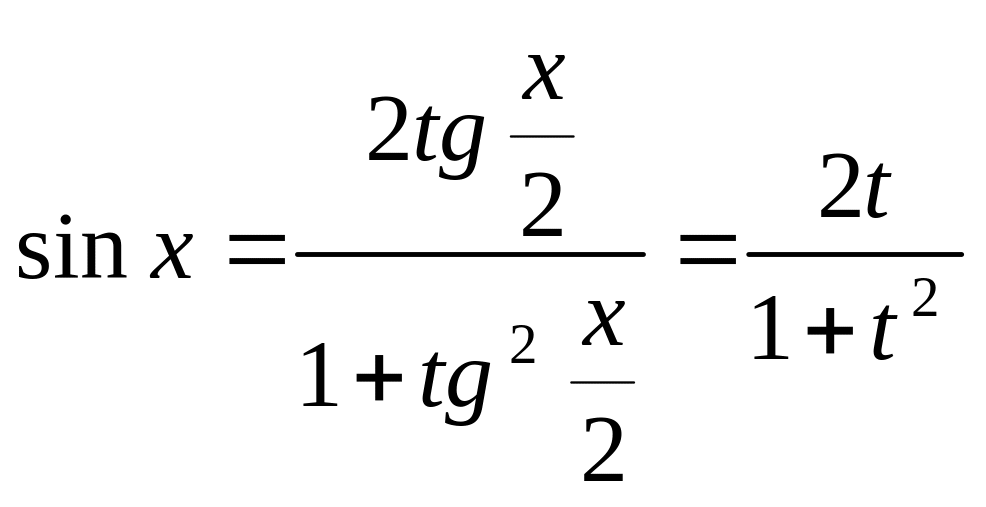В результате данной подстановки получают интеграл рацио-нальной функции от переменной :

.

Данную подстановку рекомендуется применять, если и входят в функцию в нечетной степени.

Пример 29. Найти интеграл .

Решение. Применяя подстановку , получим

в знаменателе выделим полный квадрат:

.

На практике универсальная подстановка иногда приводит к слишком сложным рациональным функциям, поэтому если функция – четная относительно синуса и косинуса, то удобнее применить подстановку , , , , .

Пример 30. Найти интеграл .

Решение. Функция является четной относительно синуса и косинуса, то есть

Применим подстановку , получим

в знаменателе выделим полный квадрат:

2.7.4 Интегралы вида

В данном случае применяют подстановку , , .

Пример 31. Найти интеграл .

Решение. Применим к данному интегралу подстановку , получим . Под знаком интеграла имеем неправильную рациональную дробь . Выделим целую часть путем деления числителя на знаменатель:

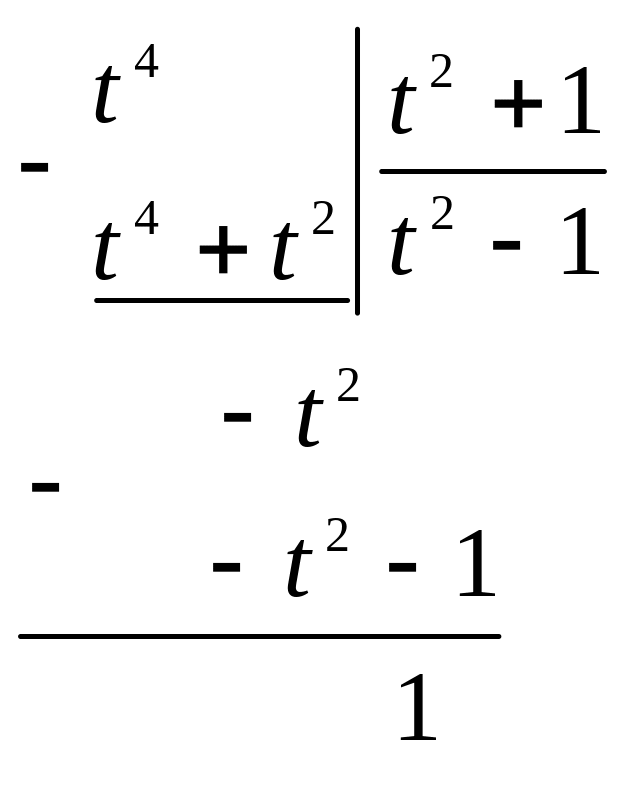
Подынтегральную функцию можно представить в виде суммы целой части и правильной рациональной дроби , а данный интеграл в виде суммы трех интегралов:

2.7.5 Интегралы вида , ,

Подынтегральные функции в данных интегралах преобразуются с помощью тригонометрических формул:

, (12)

, (13)

. (14)

Пример 32. Найти интеграл .

Решение. Применим к подынтегральной функции формулу (14), получим