1 Неопределенный интеграл

1. Понятие неопределенного интеграла

Определение 1. Функция называется первообразной функ-ции на интервале , если для любого выполняется равенство

.

Например, первообразной функции является функ-ция , так как .

Очевидно, что , где – постоянное слагаемое, также является первообразной функции , так как .

Теорема 1. Если функция является первообразной функции на , то множество всех первообразных для задается формулой , где – постоянное число.

Определение 2. Множество всех первообразных функций для называется неопределенным интегралом от функции и обозначается символом .

Таким образом, по определению

. (1)

Здесь – подынтегральная функция;

– подынтегральное выражение;

– переменная интегрирования;

– знак неопределенного интеграла.

Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.

Результат интегрирования проверяется дифференцированием.

2. Основные свойства неопределенного интеграла

1. Производная неопределенного интеграла равна подынтеграль-ной функции:

.

2. Дифференциал от неопределенного интеграла равен подын-тегральному выражению:

.

3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:

,

в частности, .

4. Постоянный множитель можно выносить за знак интеграла:

,

где – .

5. Неопределенный интеграл от алгебраической суммы конеч-ного числа непрерывных функций равен алгебраической сумме интег-ралов от каждого слагаемого:

.

6. Если и – дифференцируемая функция, то

,

то есть формула для неопределенного интеграла остается справедливой независимо от того, является ли переменная интегрирования независи-мой переменной или любой функцией, имеющей непрерывную произ-водную.

3. Правила интегрирования

Если , то

1) ;

2) ;

3) .

Пример 1.

.

Пример 2.

.

Пример 3.

.

1.4 Основные интегралы

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. ;

14. ;

15. ;

16. ;

17. ;

18. ;

19. ;

20. ;

21. .

2 ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ

2.1 Метод непосредственного интегрирования

Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции приводится к табличному интегралу, называется непосредственным интегрированием.

Пример 4. Найти интеграл .

Решение. числитель поч-ленно разделим на знаменатель и запишем данный интеграл в виде разности двух интегралов

.

Сделаем проверку, для чего найдем производную от результата интегрирования:

.

Получили подынтегральную функцию, следовательно, интеграл нашли правильно.

Пример 5. Найти интеграл .

Решение.

2.2 Метод подведения под знак дифференциала

Если подынтегральное выражение содержит некоторую функцию и ее производную, то в этом случае используют метод подведения под знак дифференциала:

. (2)

При сведении интеграла к табличному используют следующие преобразования:

,

,

,

,

,

где а и b – постоянные числа.

Например, .

Пример 6. Найти интеграл .

Решение. Заметим, что дифференциал от функции, стоящей под знаком корня, имеет вид . В подынтегральном выражении есть , то есть это . Тогда получим

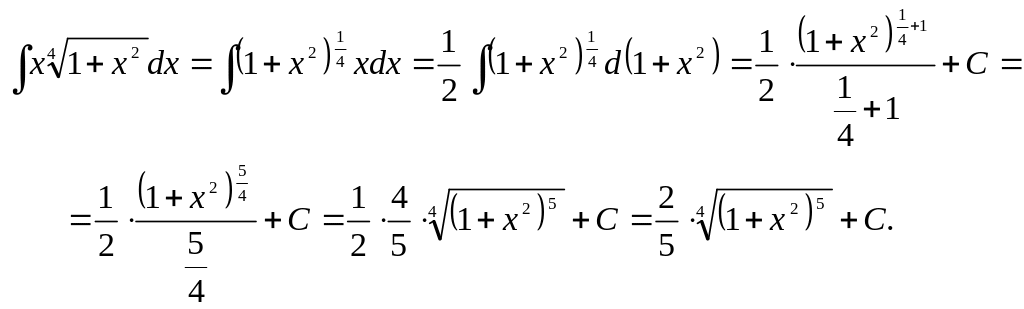
Пример 7. Найти интеграл .

Решение. Заметим, что в подынтегральном выражении есть функция и ее производная . Тогда выражение является дифференциалом функции , то есть . Используя метод подведения под знак дифференциала, найдем интеграл

.