
- •Бийский технологический институт (филиал)
- •Неопределенный и определенный интегралы
- •Требования к представлению и оформлению результатов типового расчета
- •1 Неопределенный интеграл
- •Понятие неопределенного интеграла
- •Основные свойства неопределенного интеграла
- •2.2 Метод подведения под знак дифференциала
- •2.3 Метод интегрирования подстановкой
- •2.4 Интегрирование по частям
- •2.5 Интегралы от некоторых функций, содержащих квадратный трехчлен в знаменателе
- •2.5.1 Рассмотрим интеграл
- •2.5.2 Рассмотрим интеграл вида
- •2.5.3 Рассмотрим интеграл вида
- •2.6 Интегрирование рациональных функций
- •2.6.1 Дробно-рациональная функция
- •2.6.2 Правильные рациональные дроби
- •2.6.3 Разложение правильной рациональной дроби на сумму
- •2.6.4 Интегрирование неправильных рациональных дробей
- •2.6.5 Корни знаменателя действительные и различные
- •2.6.6 Корни знаменателя действительные, среди них есть
- •2.6.7 Корни знаменателя комплексные и различные
- •2.6.8 Общий случай
- •2.7 Интегрирование тригонометрических функций
- •Интегралы вида
- •2.7.3 Интегралы вида
- •2.7.4 Интегралы вида
- •2.7.5 Интегралы вида , ,
- •2.8 Интегрирование иррациональных функций
- •2.8.2 Интеграл вида
- •3 Определенный интеграл
- •3.1 Понятие определенного интеграла
- •3.2 Геометрический смысл определенного интеграла
- •3.3 Формула Ньютона–Лейбница
- •Основные свойства определенного интеграла
- •Замена переменной в определенном интеграле
- •3.8.1 Несобственные интегралы с бесконечными пределами
- •3.8.2 Несобственные интегралы от неограниченной функции
- •Приложения определенного интеграла
- •3.9.1 Вычисление площади плоской фигуры
- •3.9.2 Площадь криволинейного сектора
- •3.9.3 Вычисление длины дуги кривой
- •4 Вопросы для самопроверки
- •5 Типовые задания
- •Литература
- •Содержание Требования к представлению и оформлению результатов типового расчета………………………………...3
- •Неопределенный и определенный интегралы
5 Типовые задания
Задание 1. Вычислить неопределенный интеграл.
а)
 ;
б)
;
б)
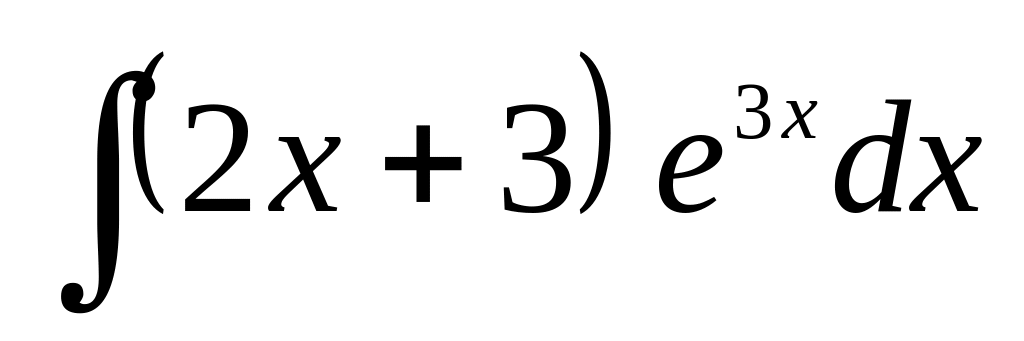 ;
в)
;
в)
 ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
ж)
;
ж)
![]() .
.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() .
.
а)
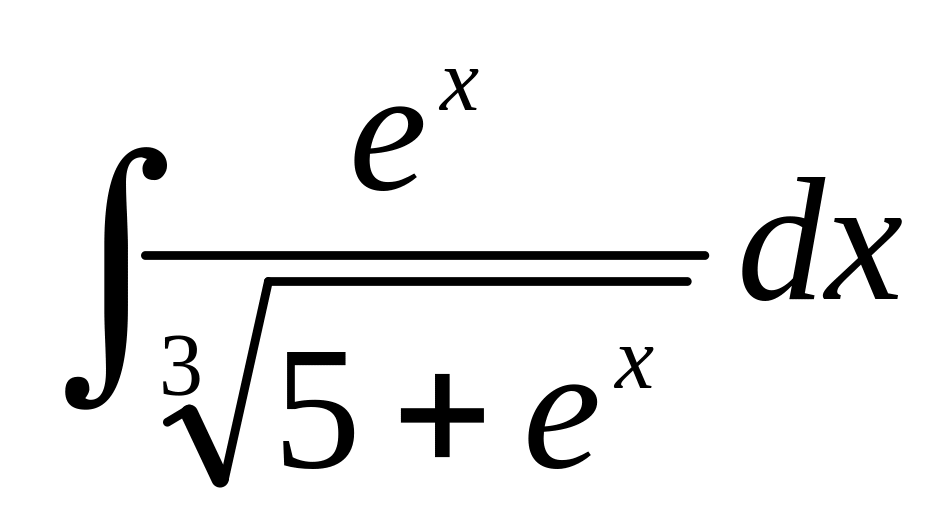 ;
б)
;
б)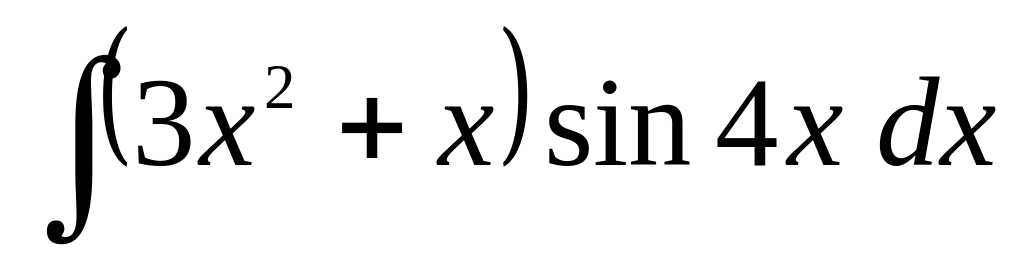 ;
в)
;
в)
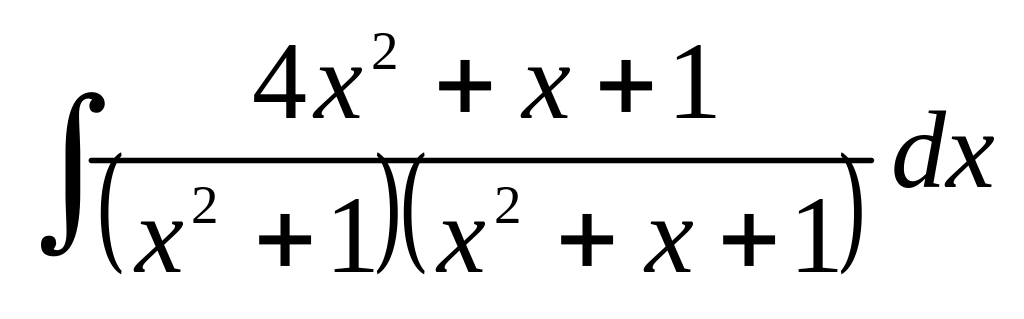 ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
ж)
;
ж)
![]() .
.
а)
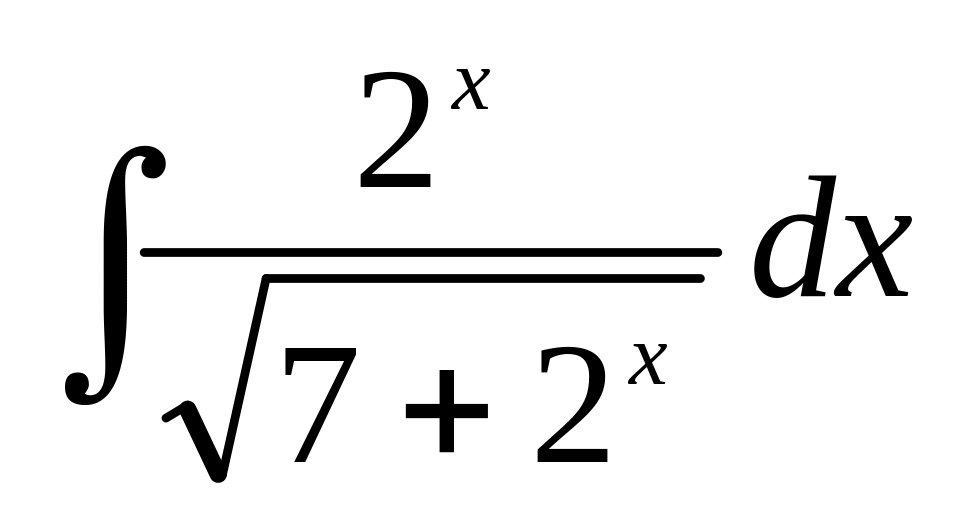 ;
б)
;
б)
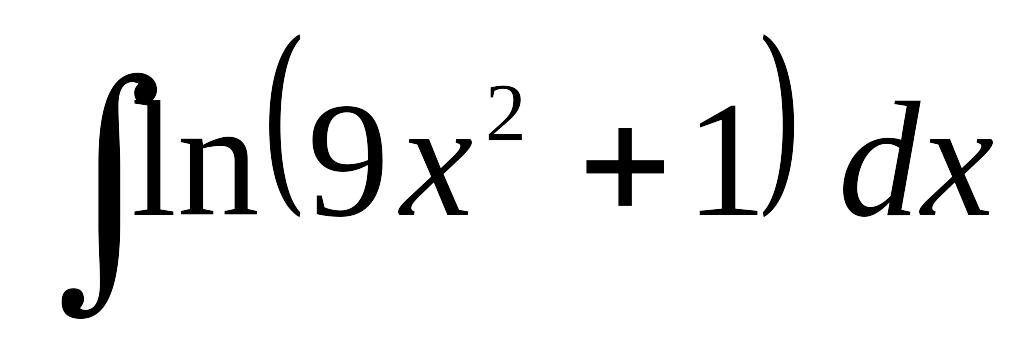 ;
в)
;
в)
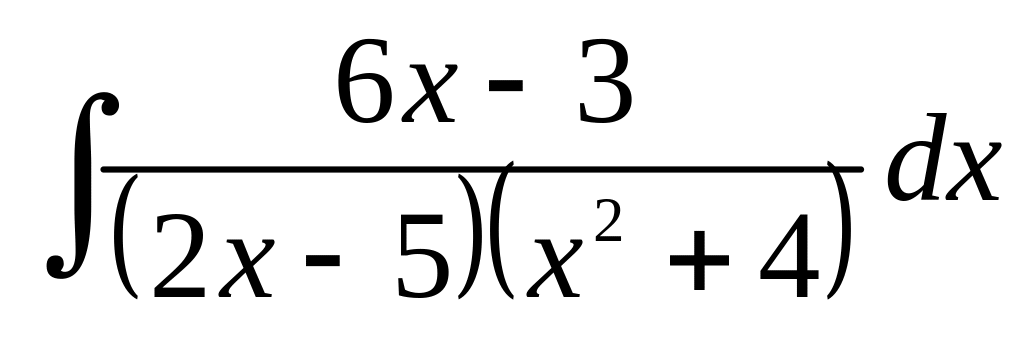 ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() .
.
а)
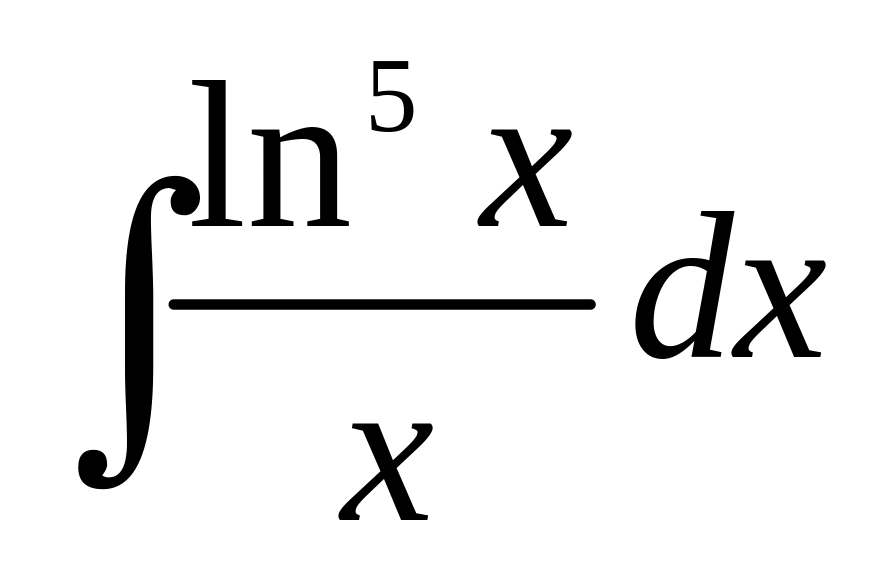 ;
б)
;
б)
 ;
в)
;
в)
 ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() .
.
а)
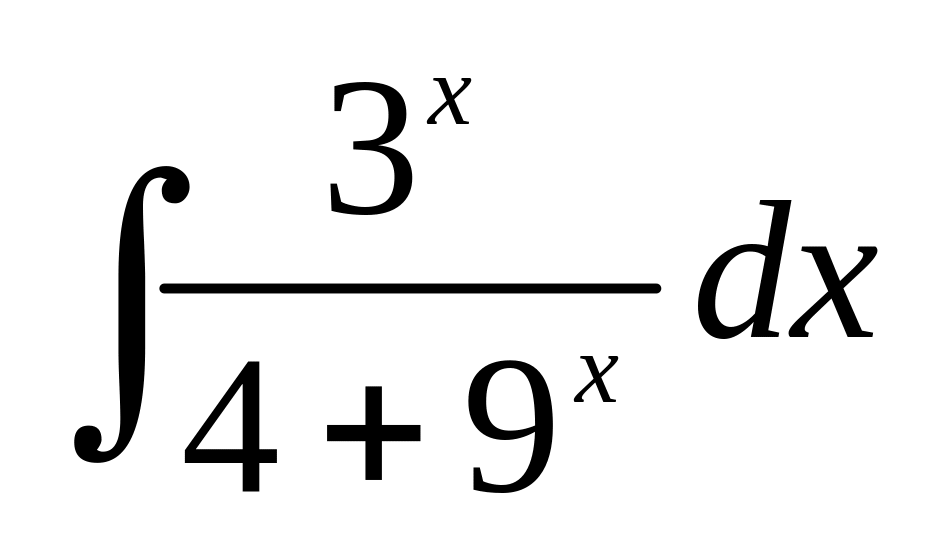 ;
б)
;
б)
 ;
в)
;
в)
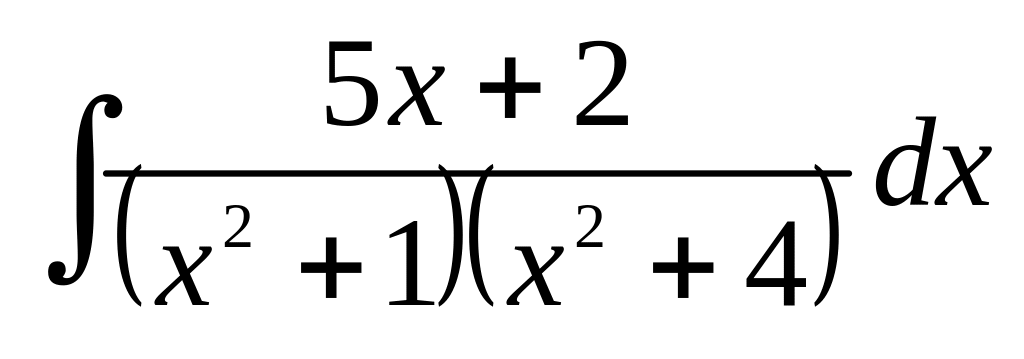 ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() .
.
а)
 ;
б)
;
б)
 ;
в)
;
в)
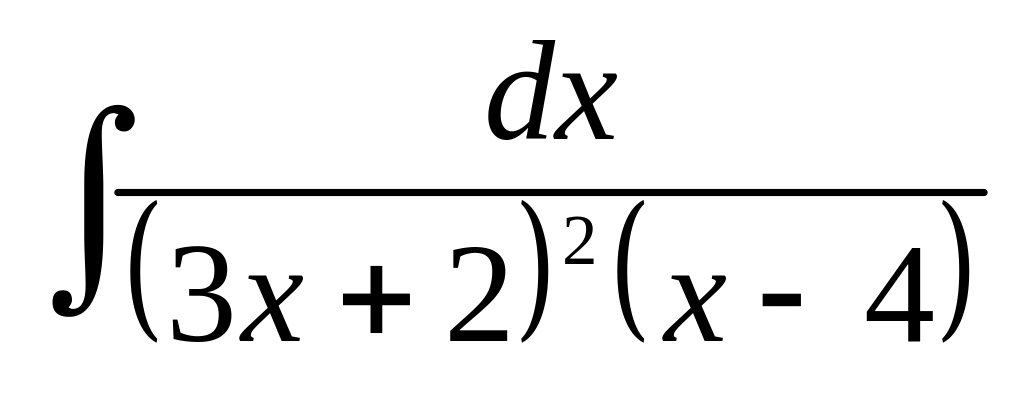 ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() .
.
а)
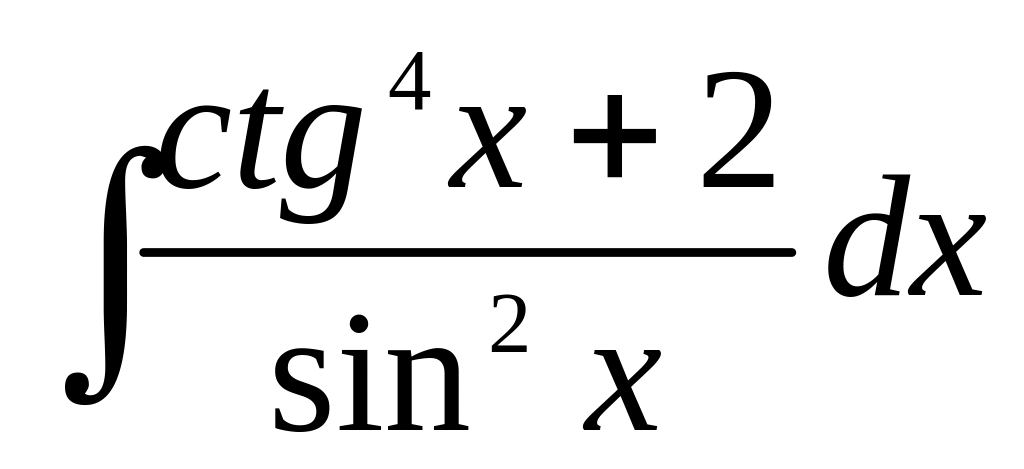 ;
б)
;
б)
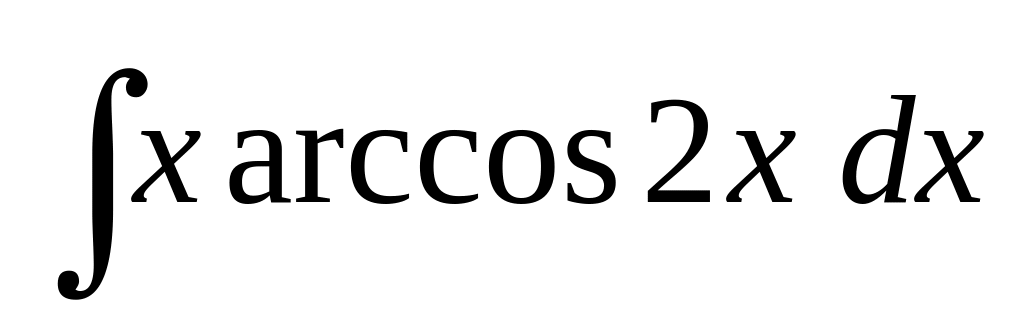 ;
в)
;
в)
 ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() .
.
а)
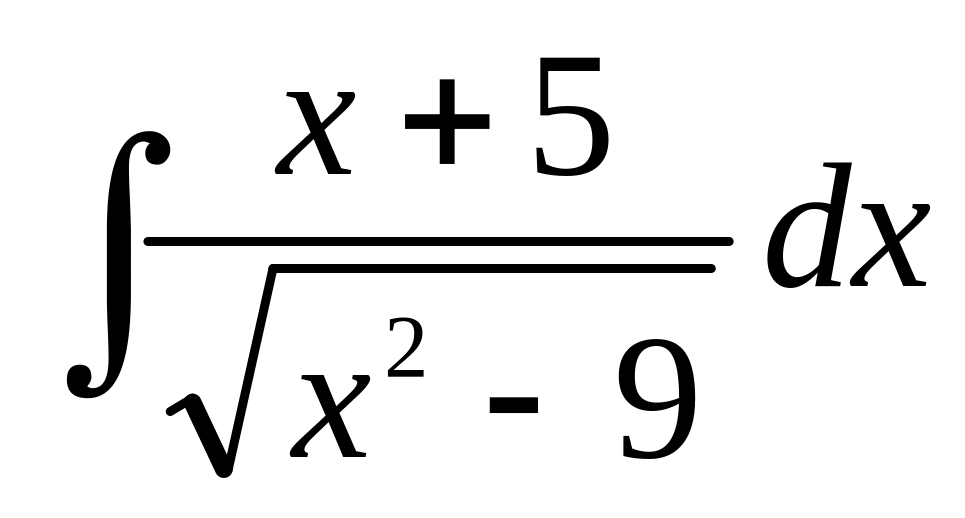 ;
б)
;
б)
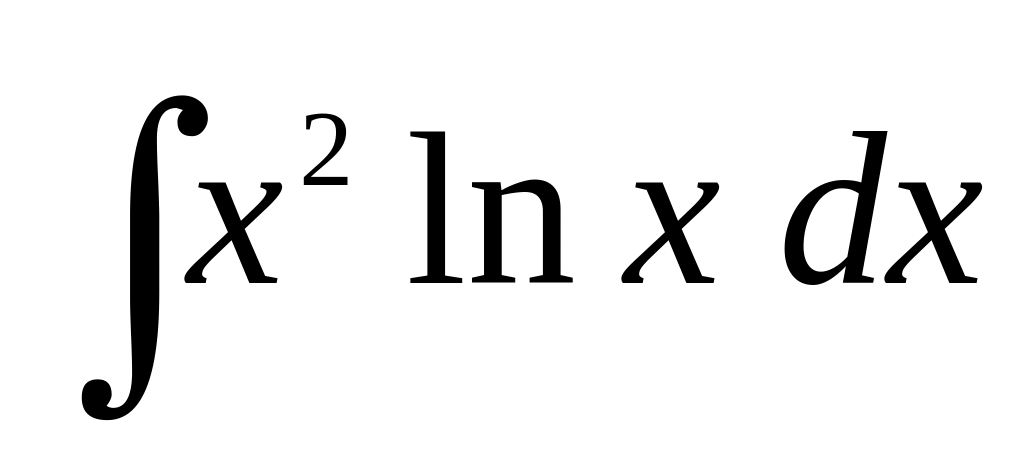 ;
в)
;
в)
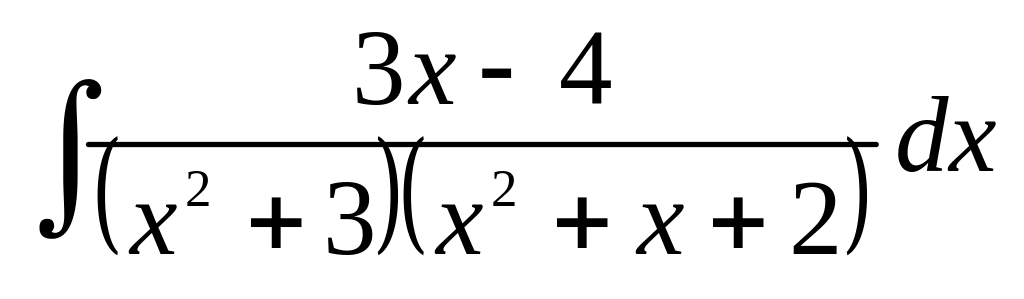 ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)![]() ;
;
ж)
![]() .
.
а)
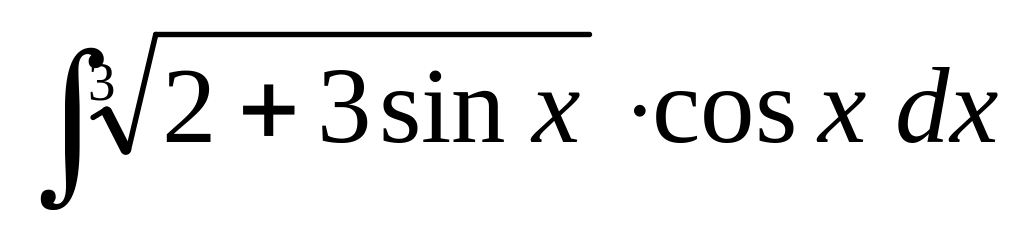 ;
б)
;
б)
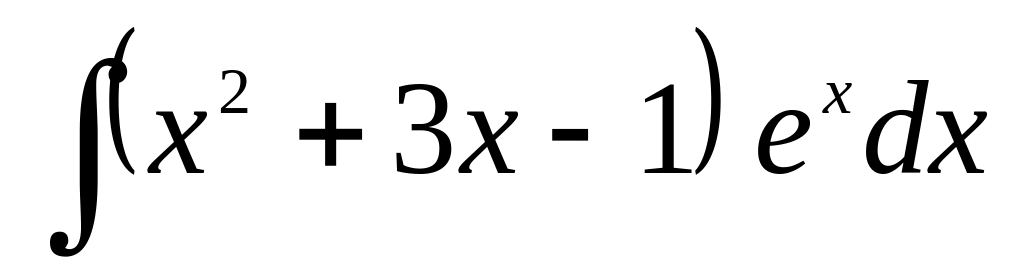 ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() ;
;
е)
![]() ;
ж)
;
ж)
![]() .
.
а)
 ;
б)
;
б)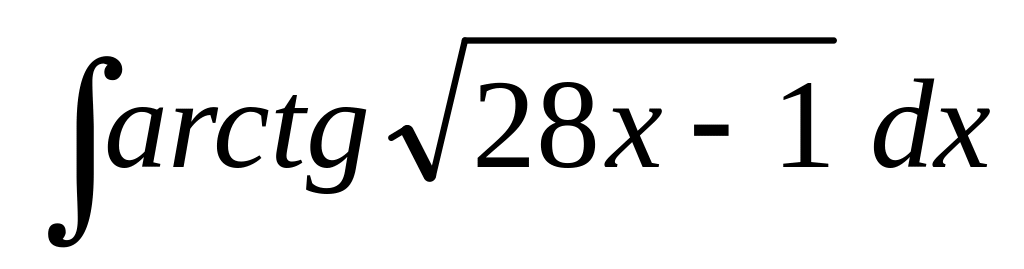 ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() ;
;
е)
![]() ;
ж)
;
ж)
![]() .
.
а)
 ;
б)
;
б)
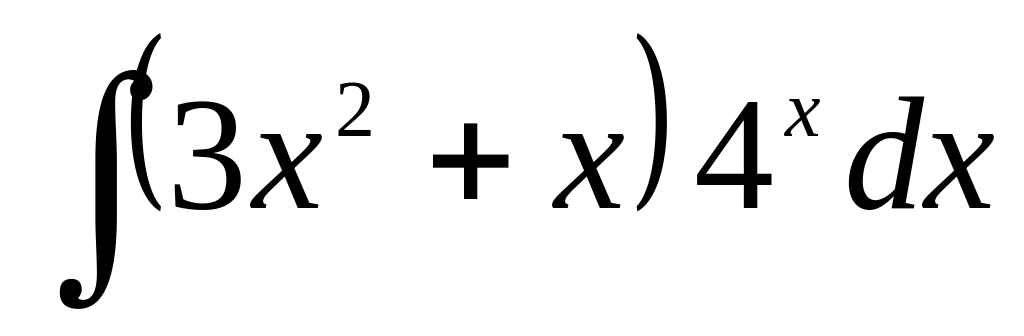 ;
в)
;
в)
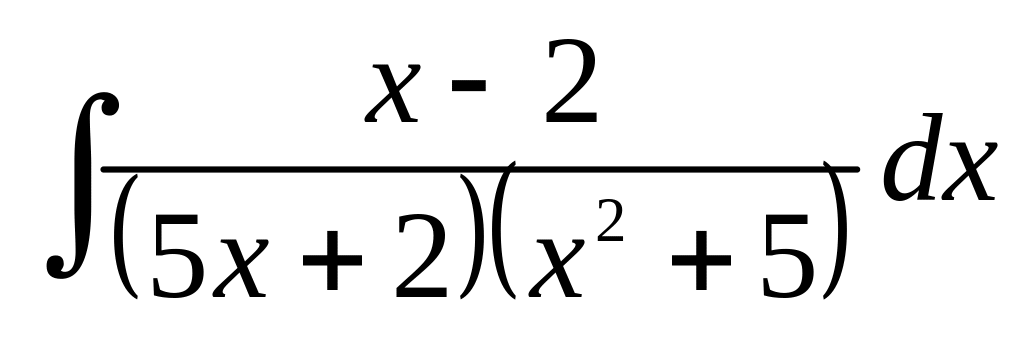 ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() .
.
а)
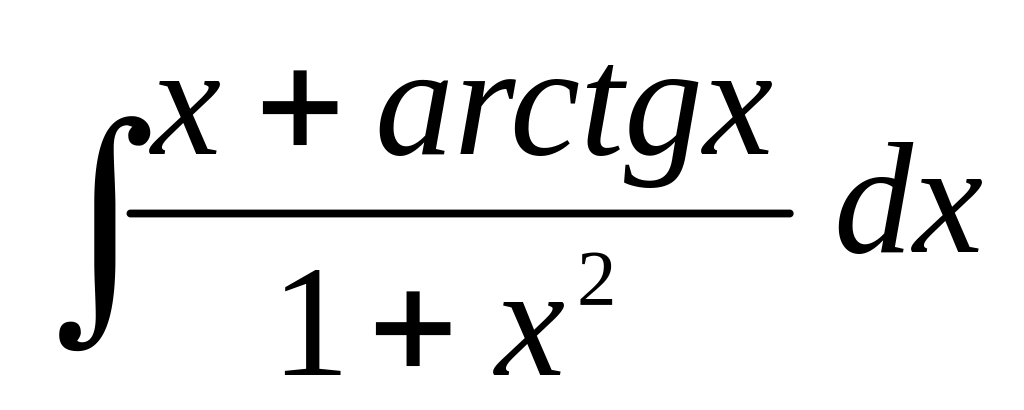 ;
б)
;
б)
 ;
в)
;
в)
 ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() .
.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() .
.
а)
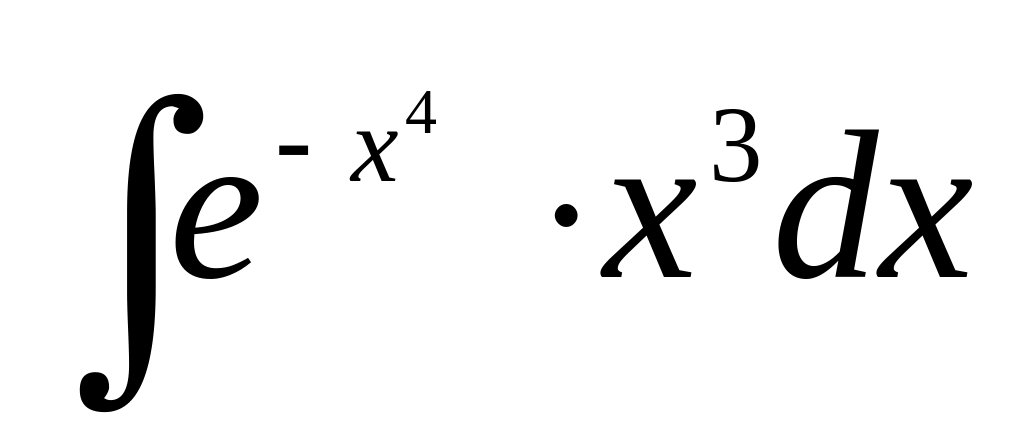 ;
б)
;
б)
 ;
в)
;
в)
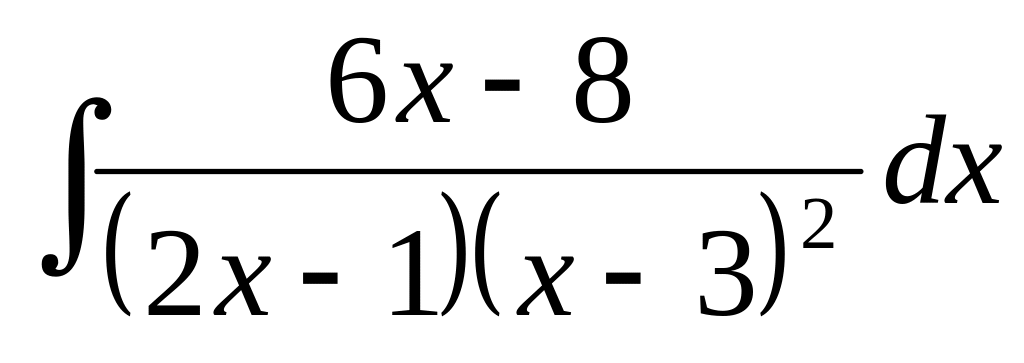 ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() .
.
а)
 ;
б)
;
б)
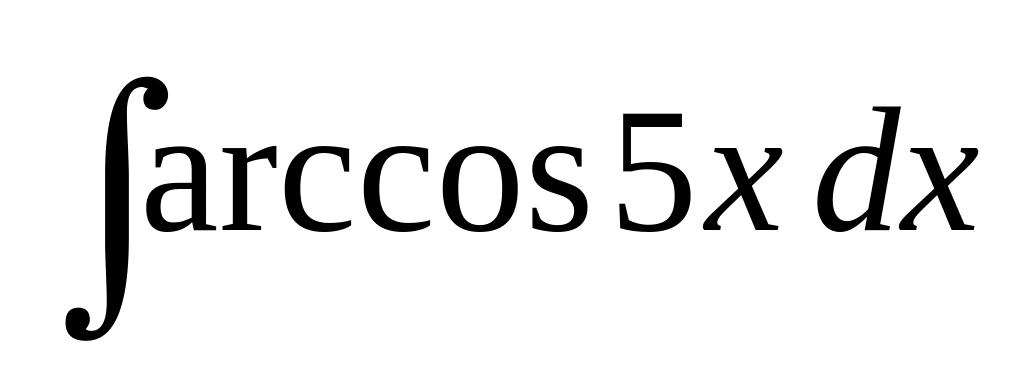 ;
в)
;
в)
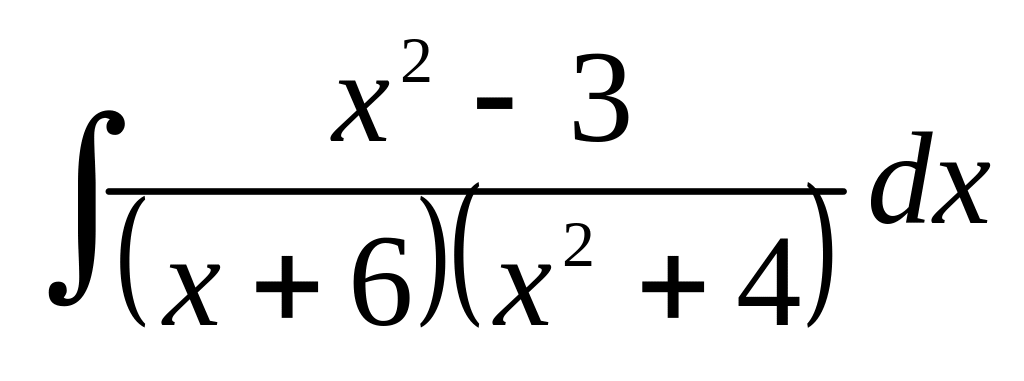 ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() .
.
а)
 ;
б)
;
б)
 ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() ;
;
е)
![]() ;
ж)
;
ж)
![]() .
.
а)
 ;
б)
;
б)
 ;
;
в)
![]() ;
г)
;
д)
;
г)
;
д)
![]() ;
;
е)
![]() ;
ж)
;
ж)
![]() .
.
а)
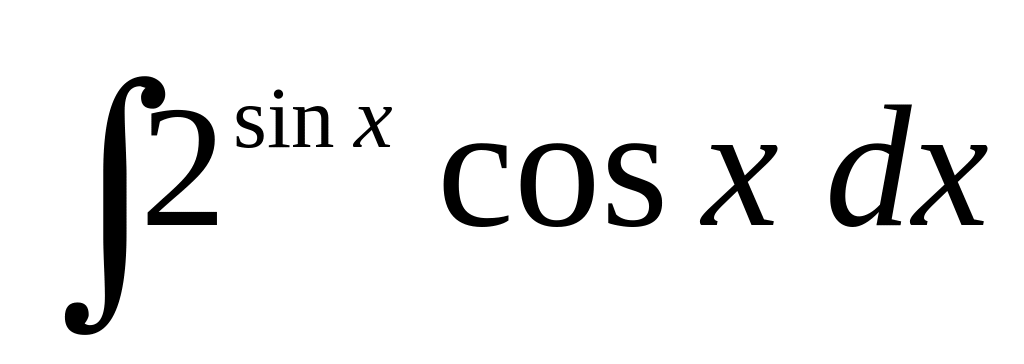 ;
б)
;
б)
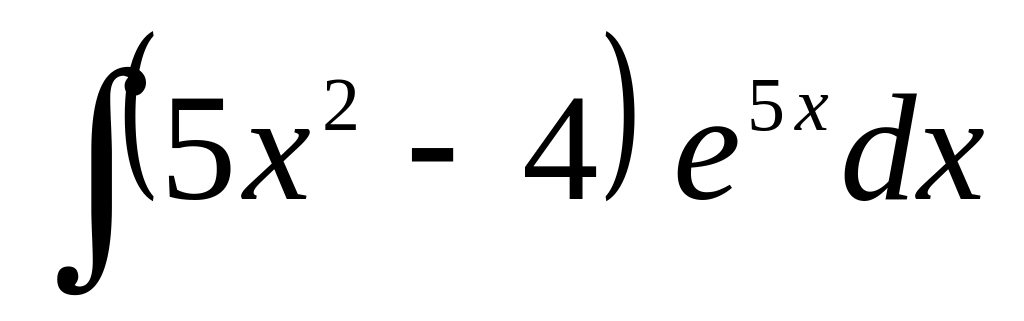 ;
в)
;
в)
 ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() .
.
а)
 ;
б)
;
б)
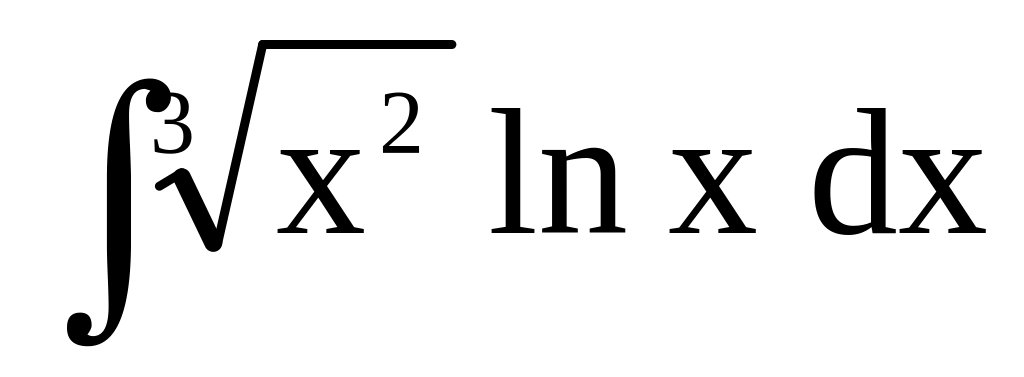 ;
в)
;
в)
 ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() .
.
а)
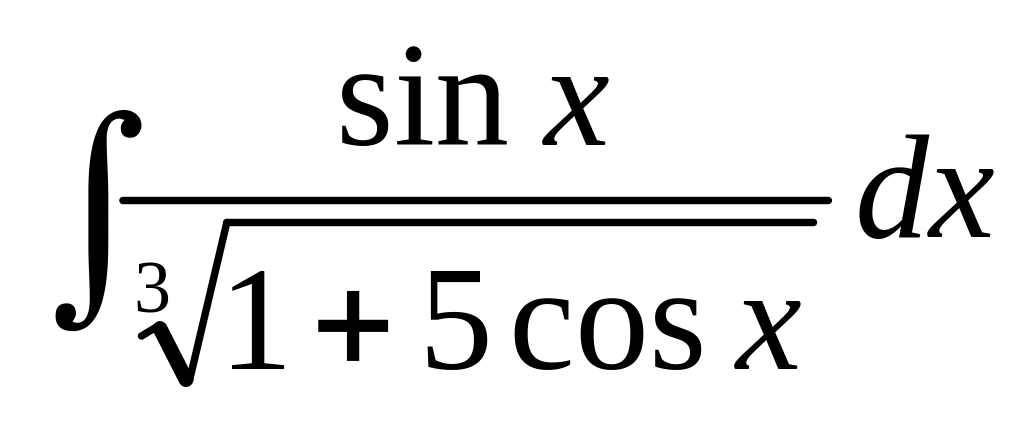 ;
б)
;
б)
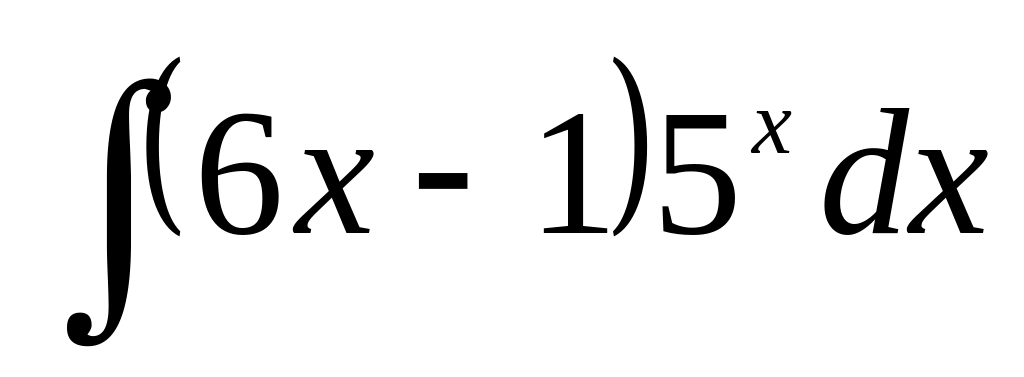 ;
в)
;
в)
 ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() .
.
а)
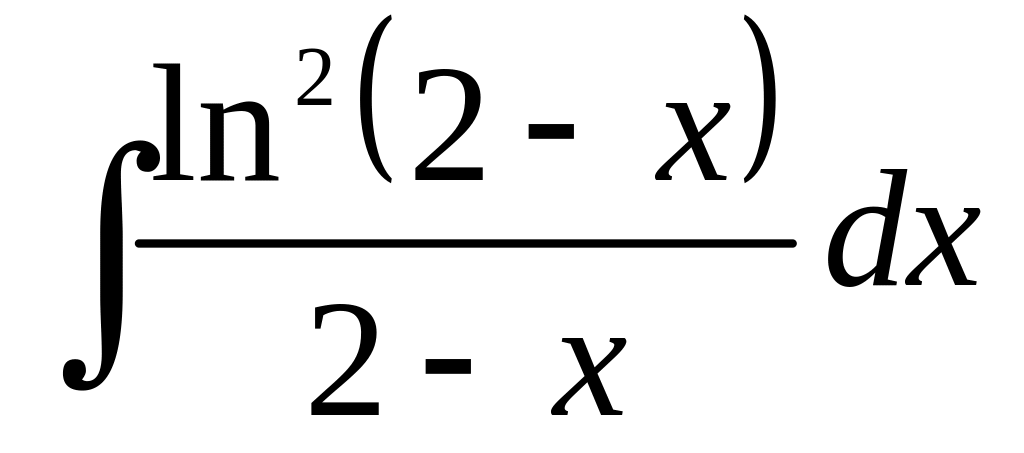 ;
б)
;
б)
 ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() ;
;
е)
![]() ;
ж)
;
ж)
![]() .
.
а)
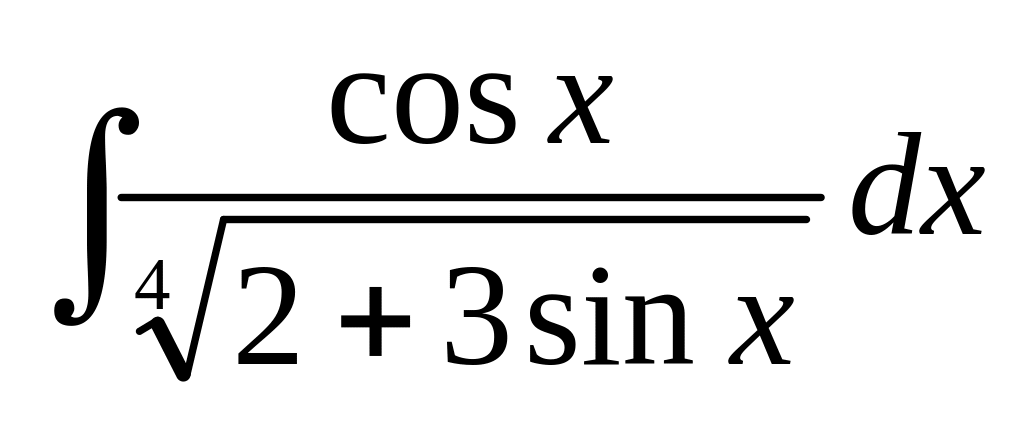 ;
б)
;
б)
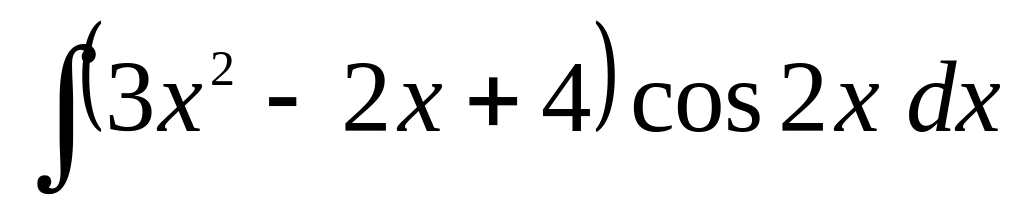 ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() ;
;
е)
![]() ;
ж)
;
ж)
![]() .
.
а)
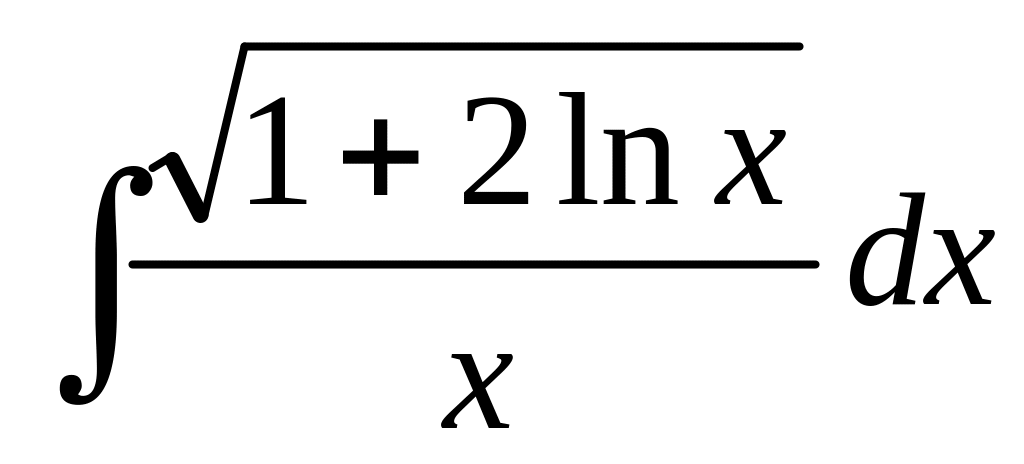 ;
б)
;
б)
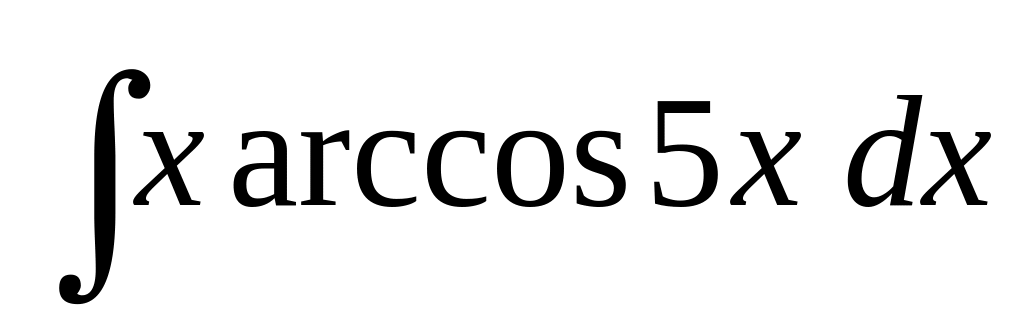 ;
в)
;
в)
 ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() .
.
а)
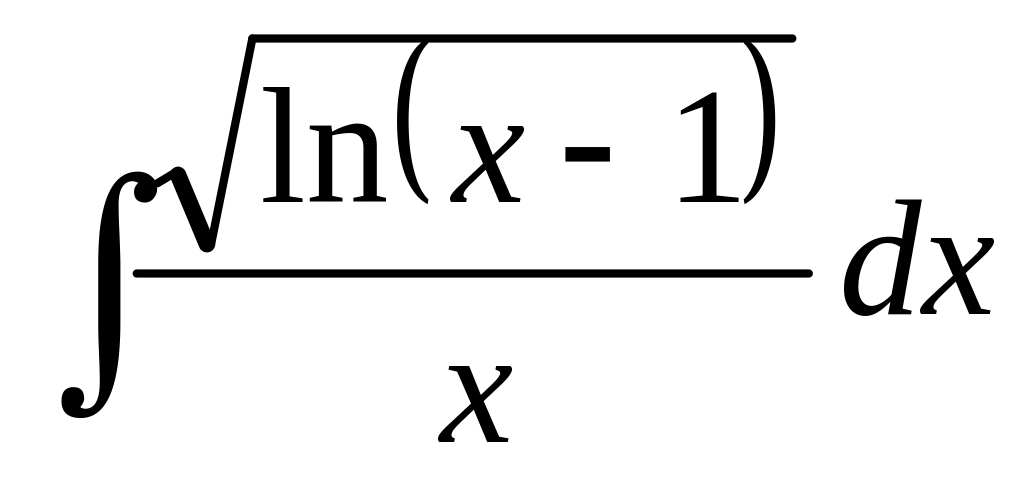 ;
б)
;
б)
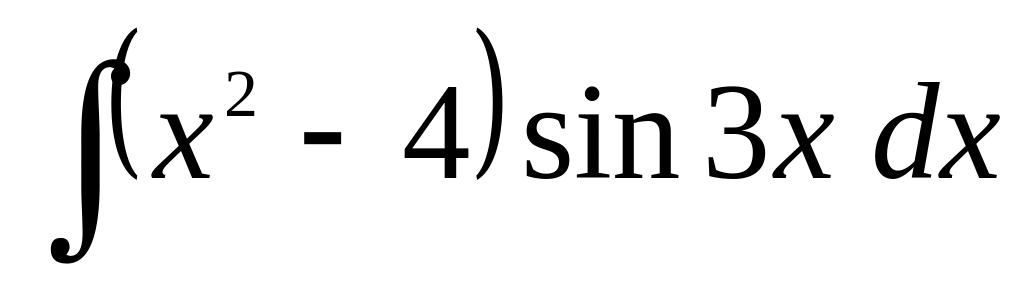 ;
в)
;
в)
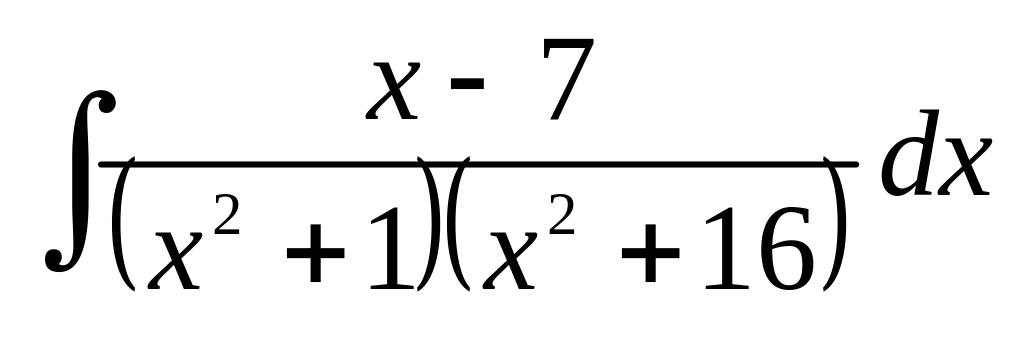 ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() .
.
а)
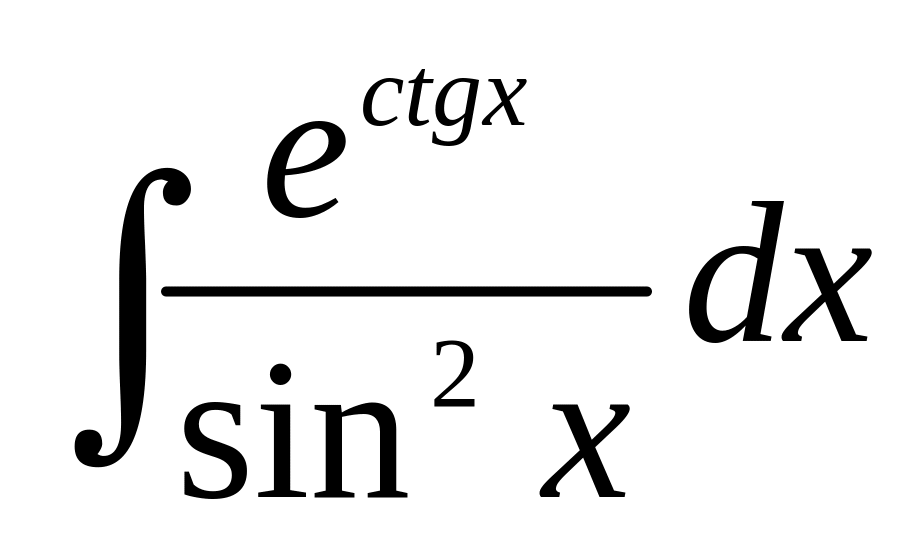 ;
б)
;
б)
 ;
в)
;
в)
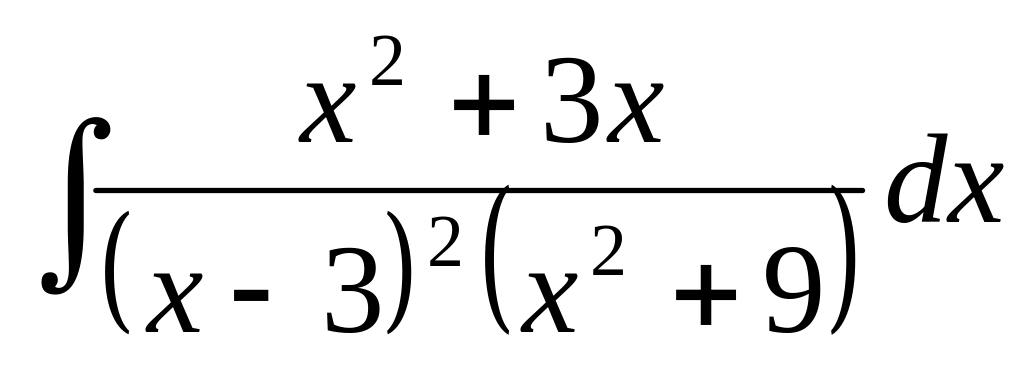 ;
;
г)
![]() ;
д)
;
д)
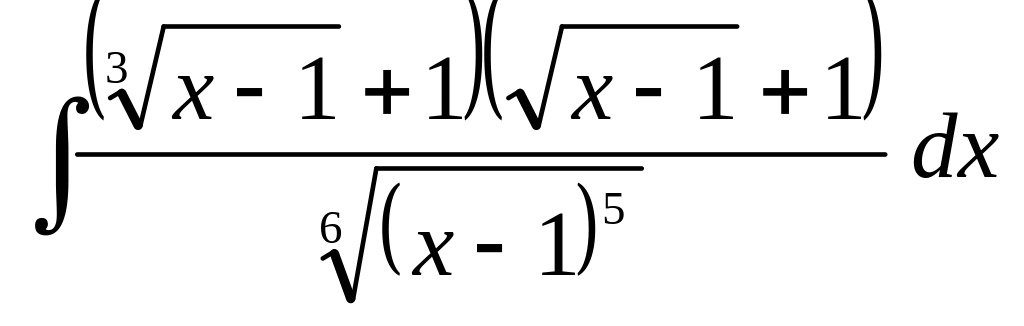 ;
;
е)
![]() ;
ж)
;
ж)
![]() .
.
а)
 ;
б)
;
б)
 ;
в)
;
в)
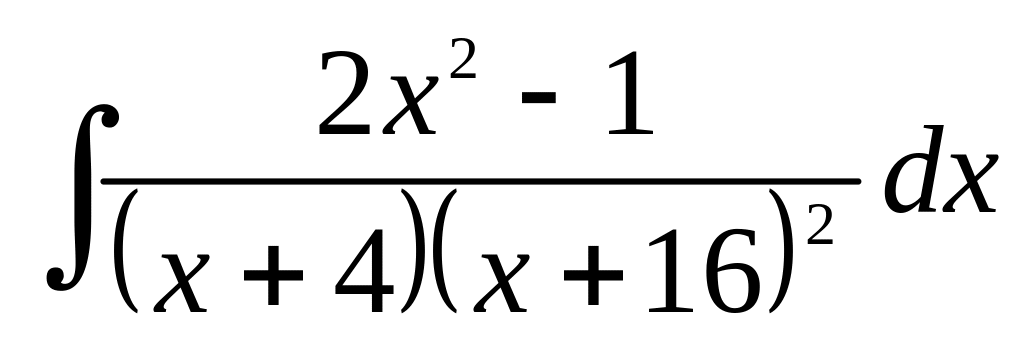 ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() .
.
а)
 ;
б)
;
б)
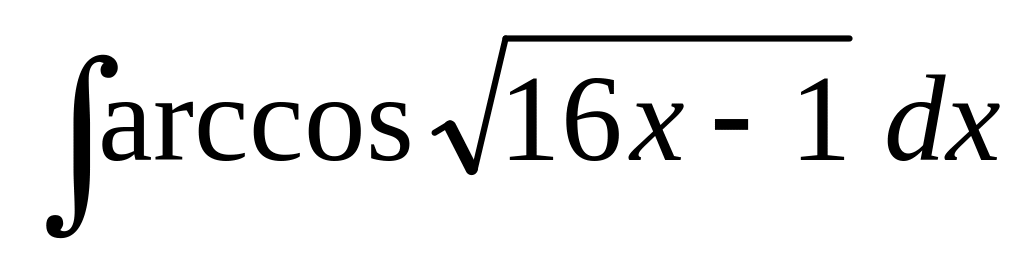 ;
в)
;
в)
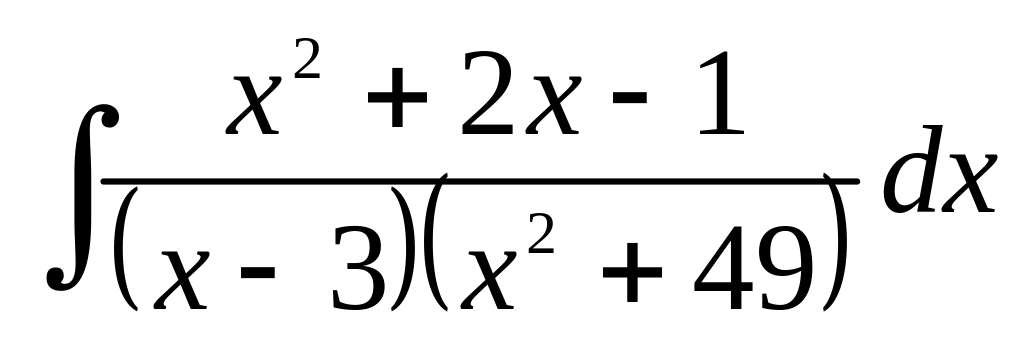 ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)![]() ;
;
ж)
![]() .
.
а)
 ;
б)
;
б)
 ;
в)
;
в)
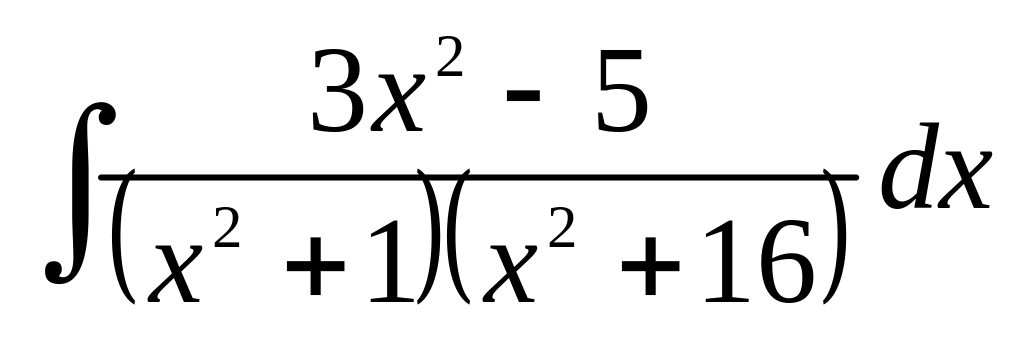 ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() .
.
а)
 ;
б)
;
б)
 ;
в)
;
в)
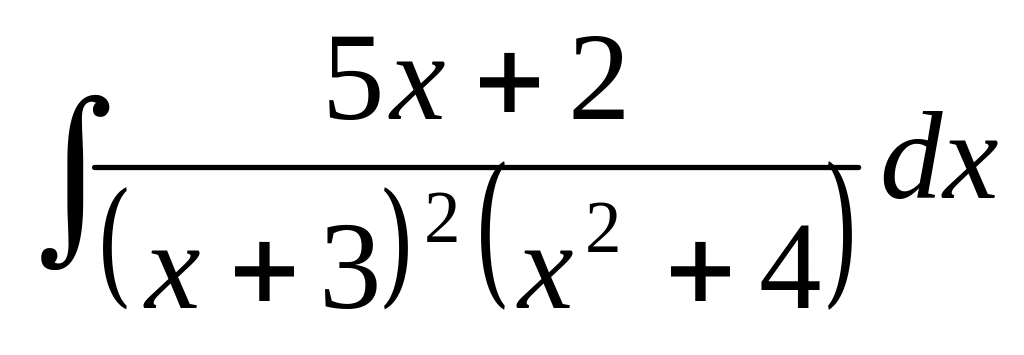 ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() .
.
Задание 2. Вычислить определенный интеграл:
а)
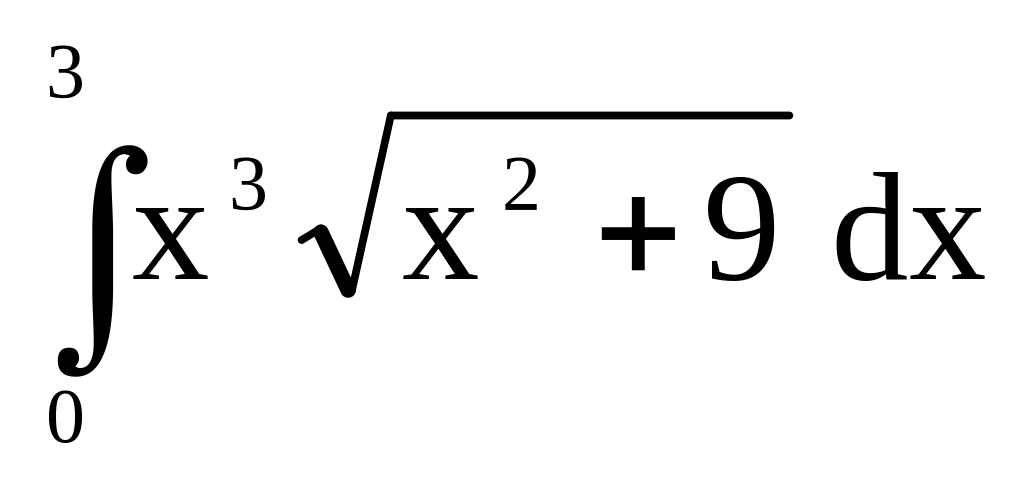 ;
б)
;
б)
 .
.а)
 ;
б)
;
б)
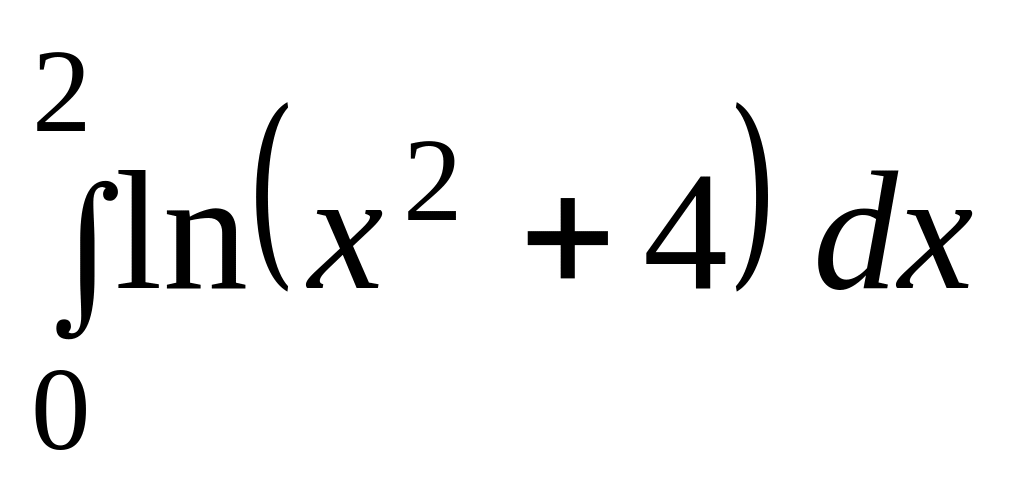 .
.а)
 ;
б)
;
б)
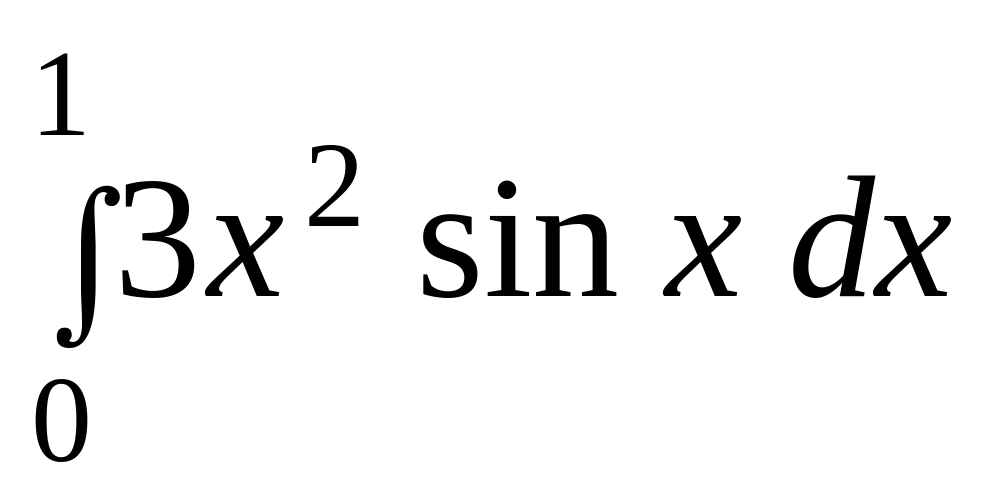 .
.а)
 ;
б)
;
б)
 .
.а)
 ;
б)
.
;
б)
.а)
 ;
б)
;
б)
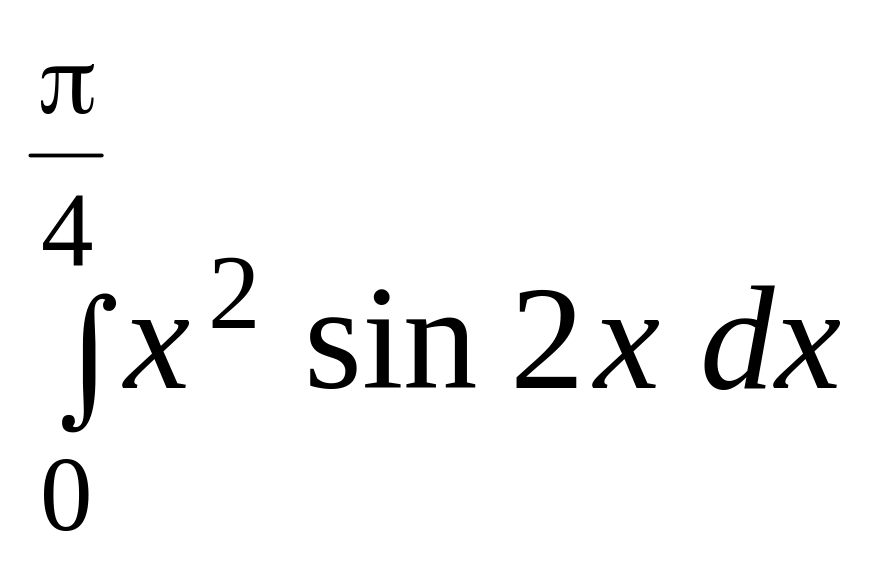 .
.а)
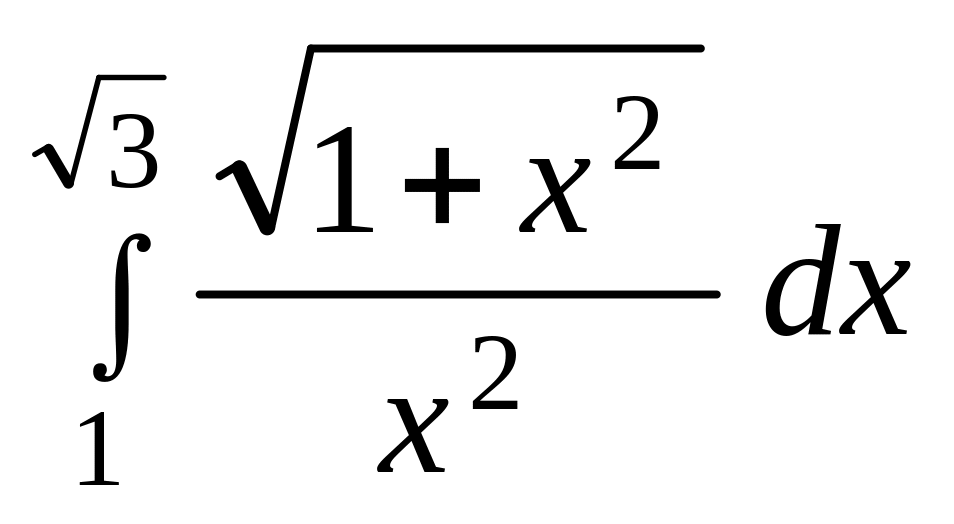 ;
б)
;
б)
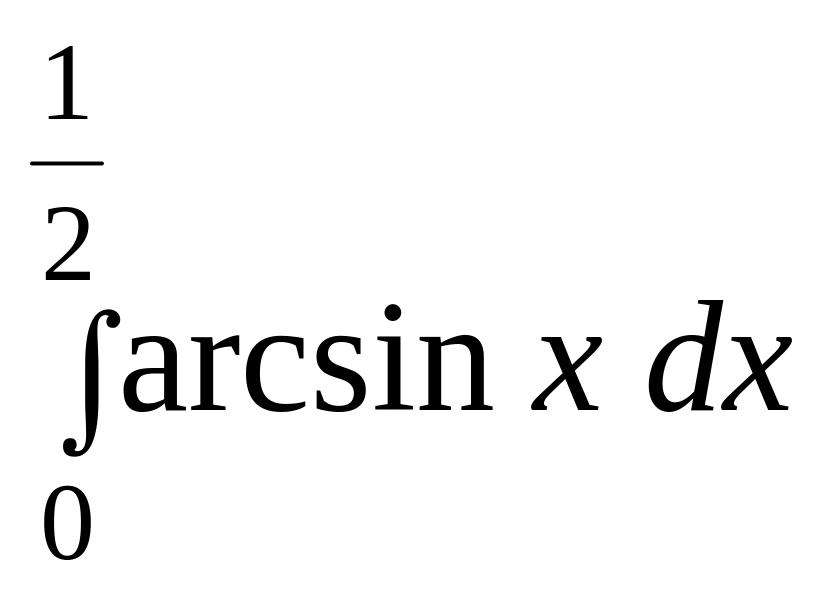 .
.а)
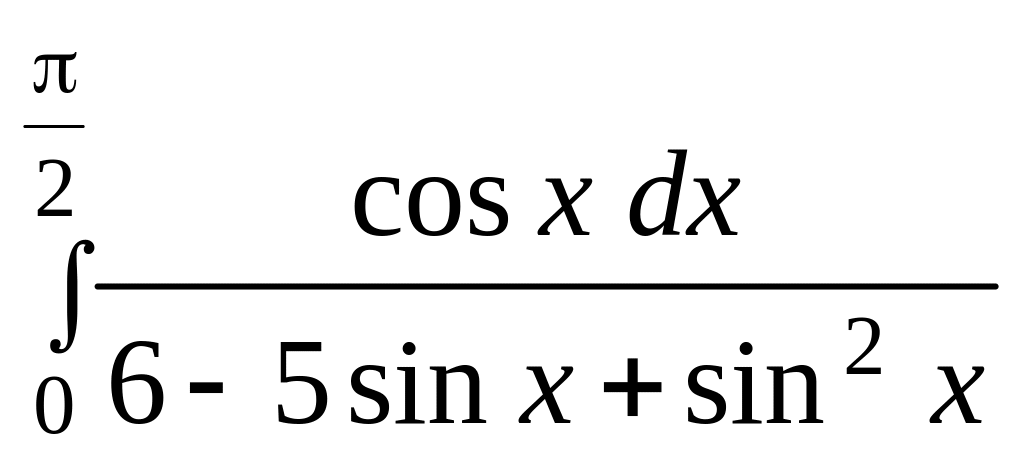 ;
б)
;
б)
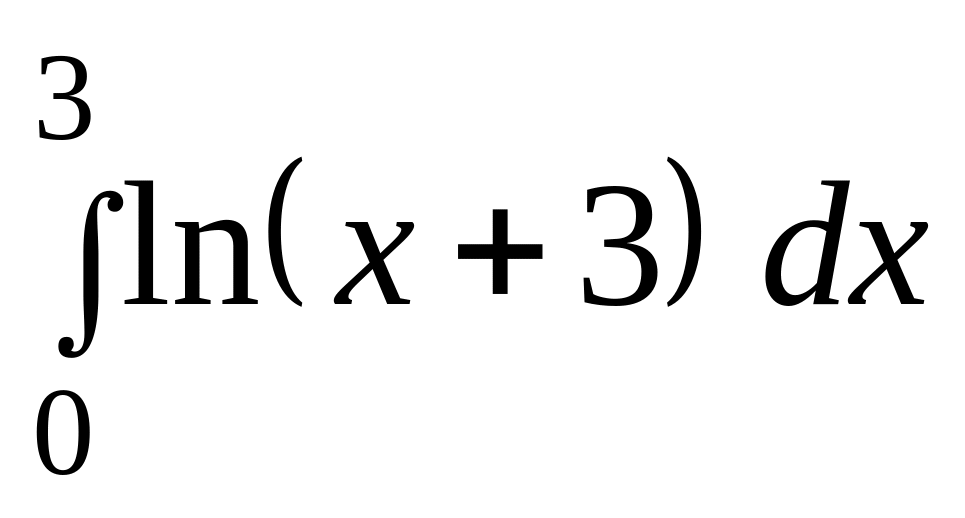 .
.а)
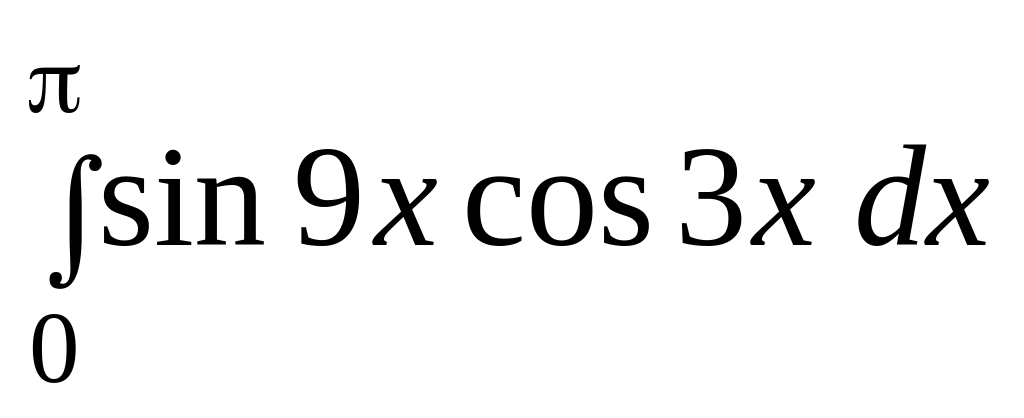 ;
б)
;
б)
 .
.а)
 ;
б)
;
б)
 .
.а)
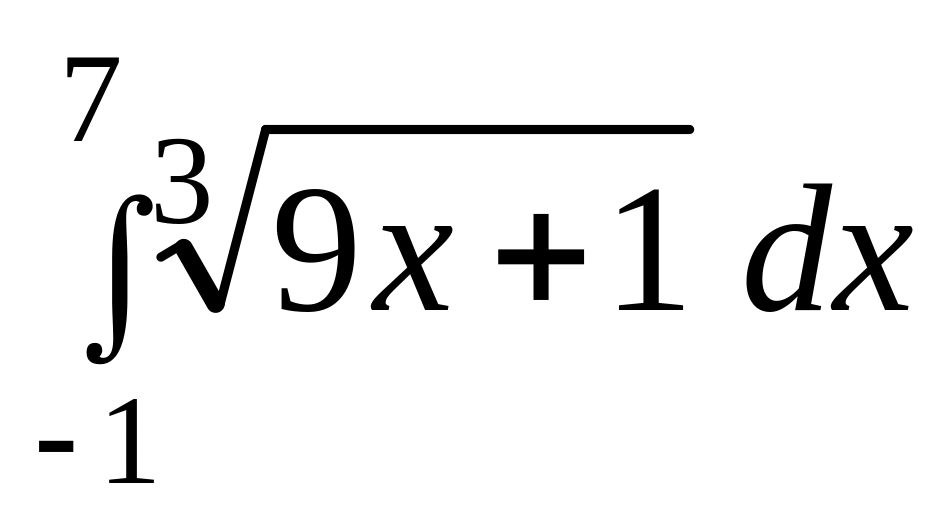 ;
б)
;
б)
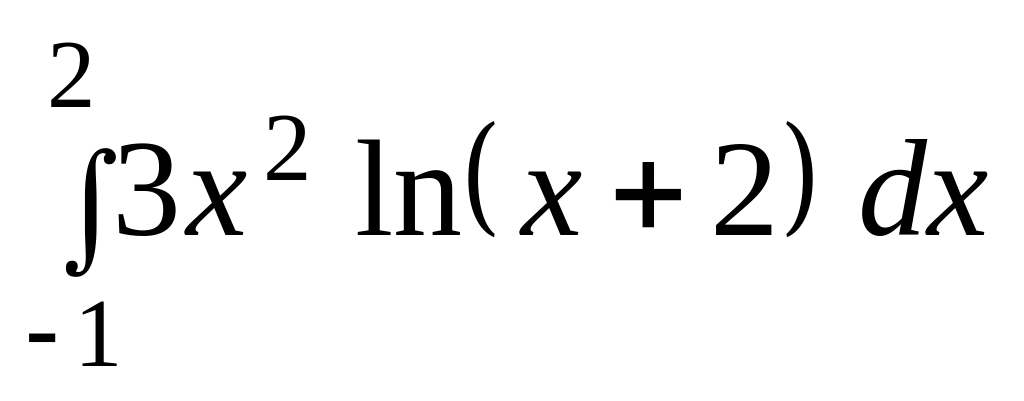 .
.а)
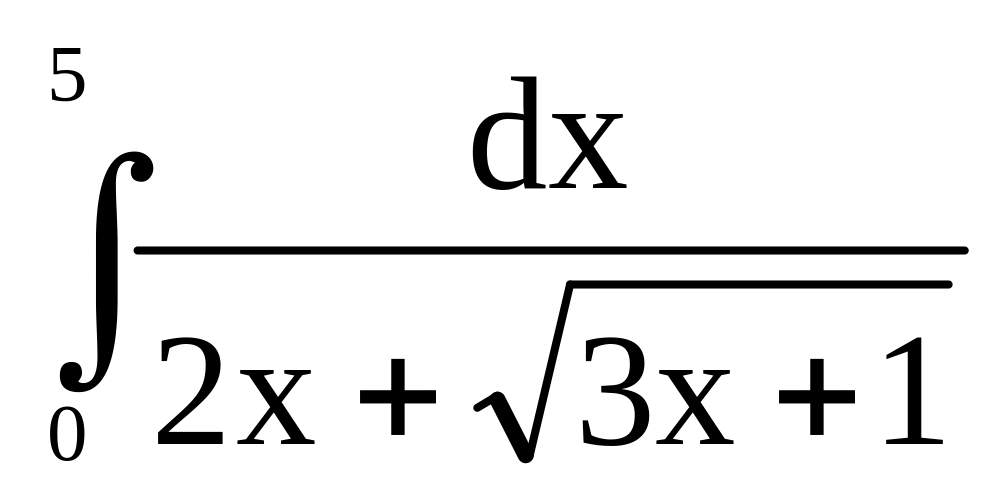 ;
б)
;
б)
 .
.а)
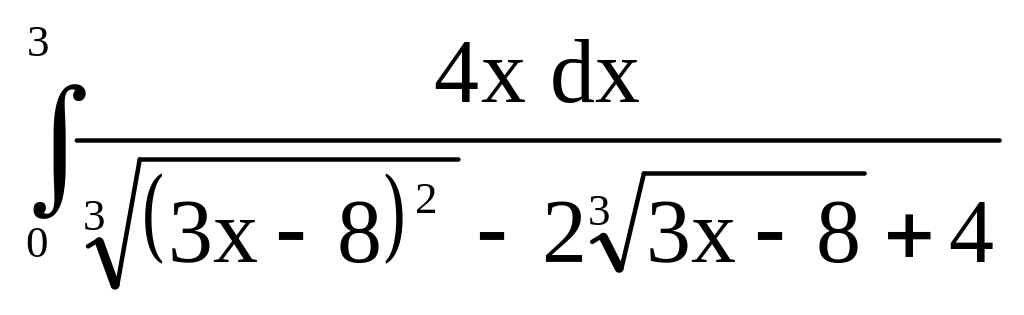 ;
б)
;
б)
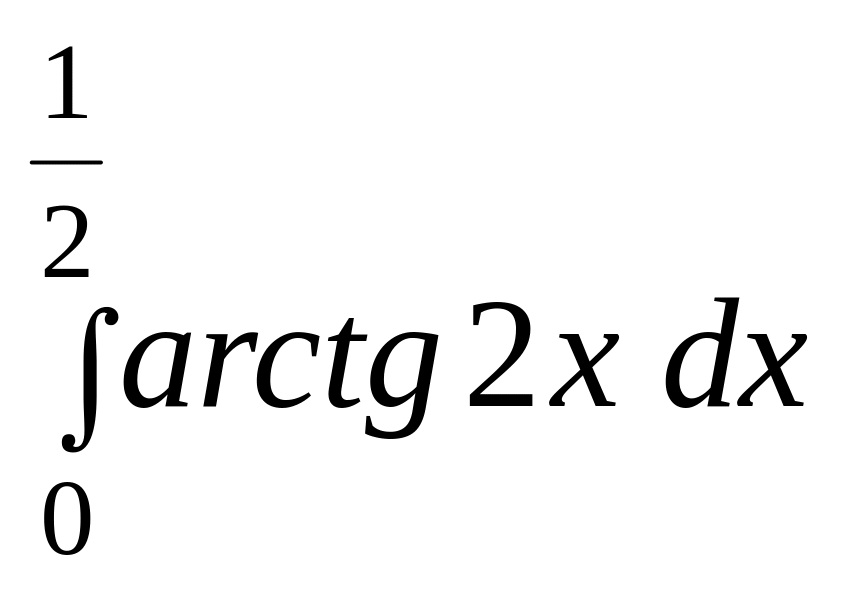 .
.а)
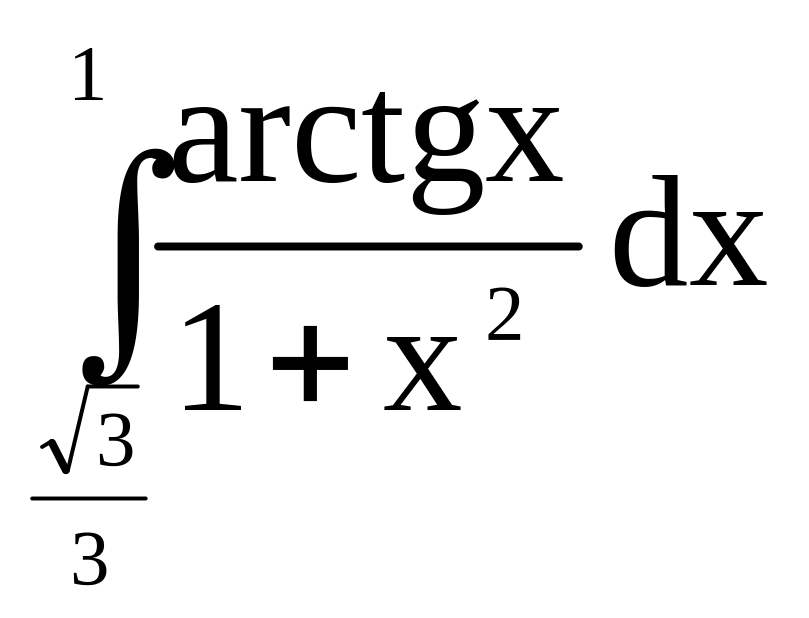 ;
б)
;
б)
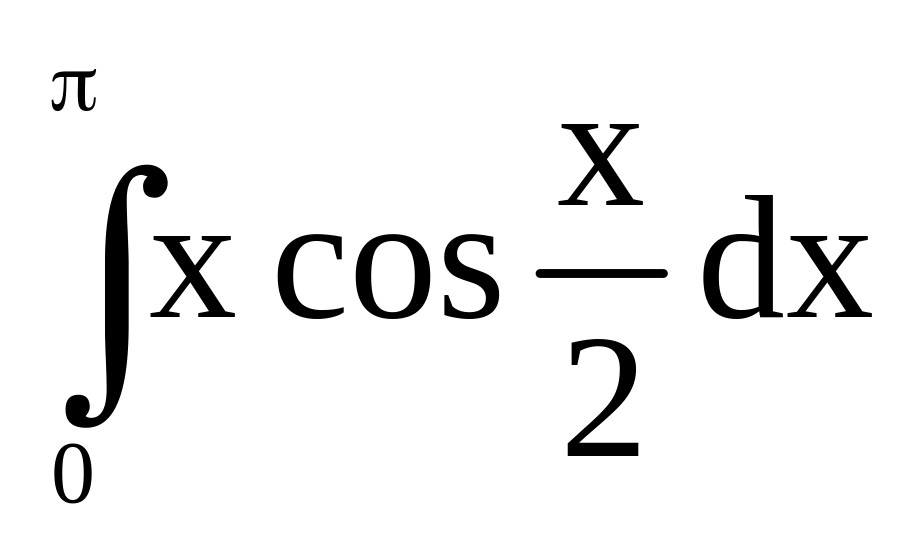 .
.а)
 ;
б)
.
;
б)
.а)
 ;
б)
;
б)
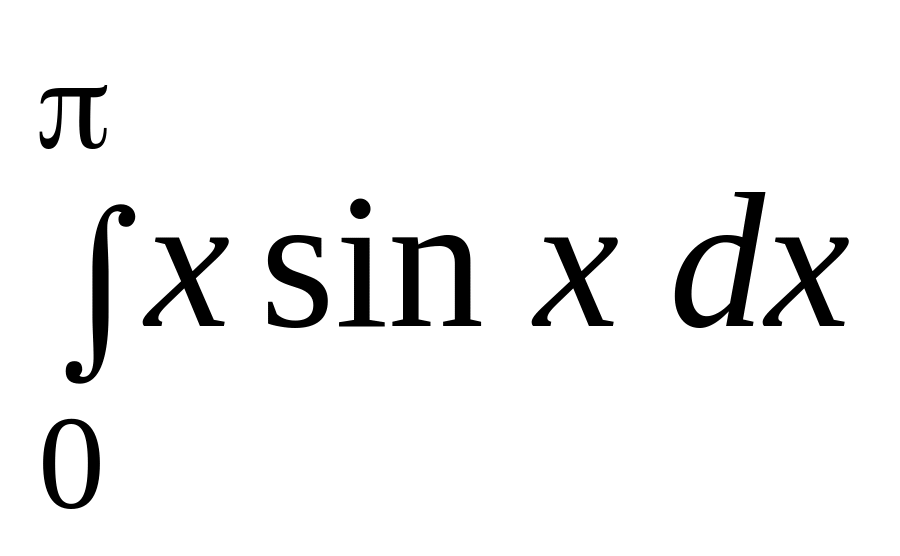 .
.а)
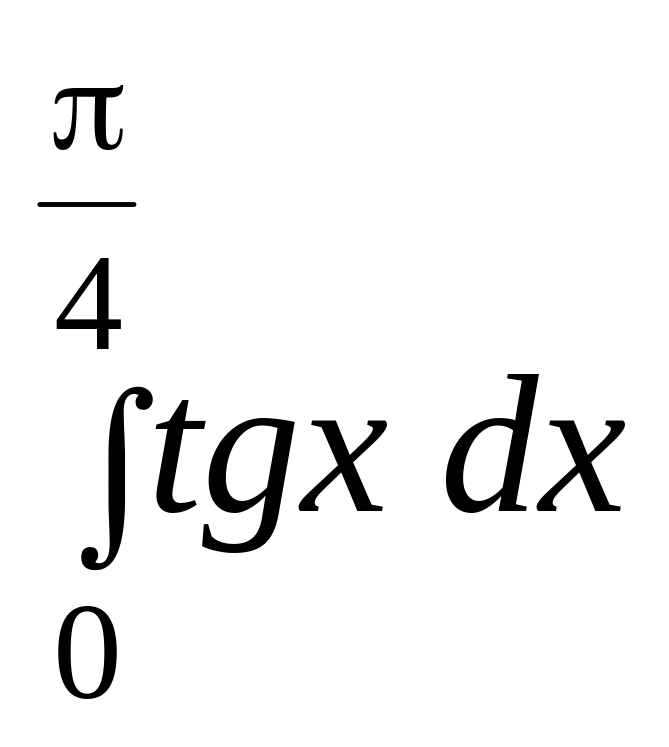 ;
б)
;
б)
 .
.а)
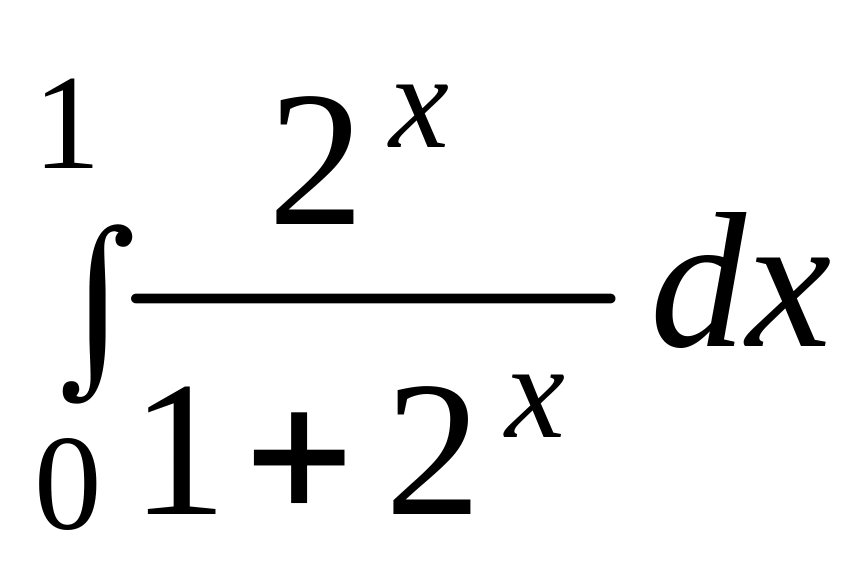 ;
б)
;
б)
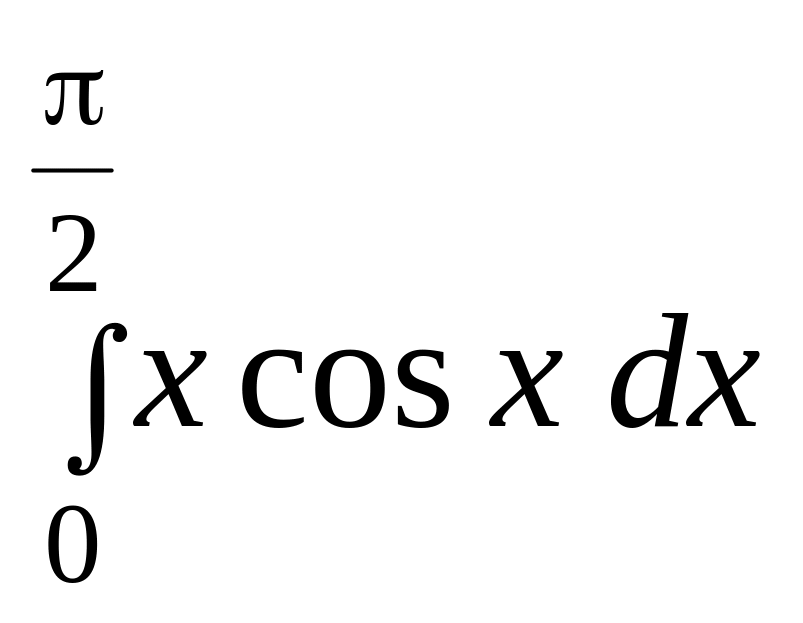 .
.а)
 ;
б)
;
б)
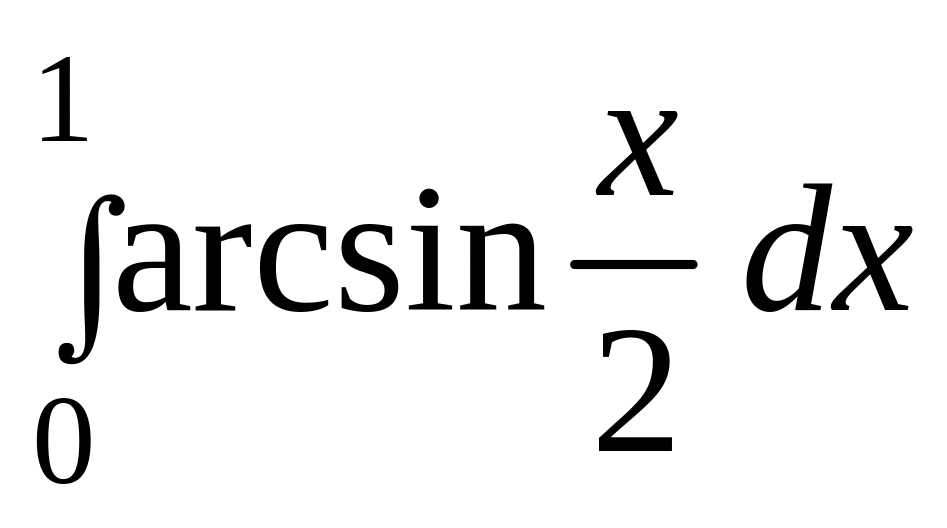 .
.а)
 ;
б)
;
б)
 .
.а)
 ;
б)
;
б)
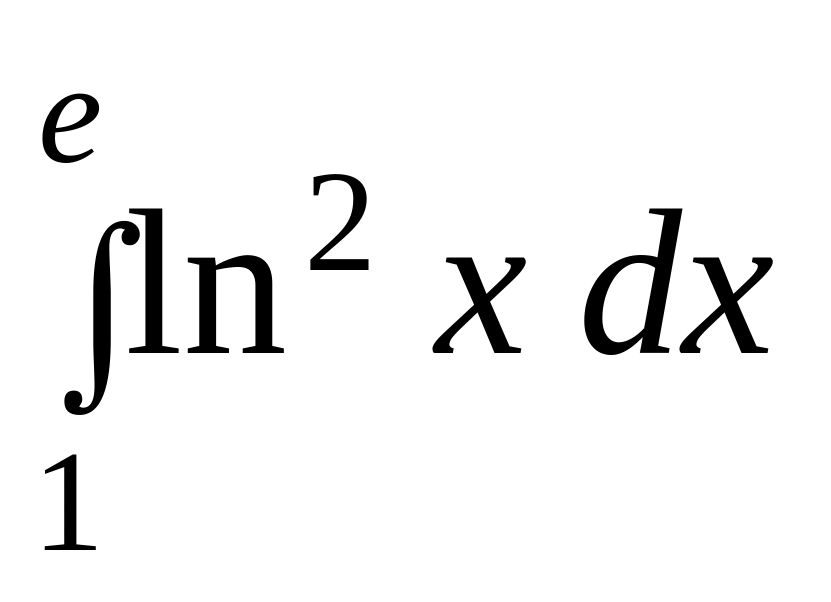 .
.а)
 ;
б)
;
б)
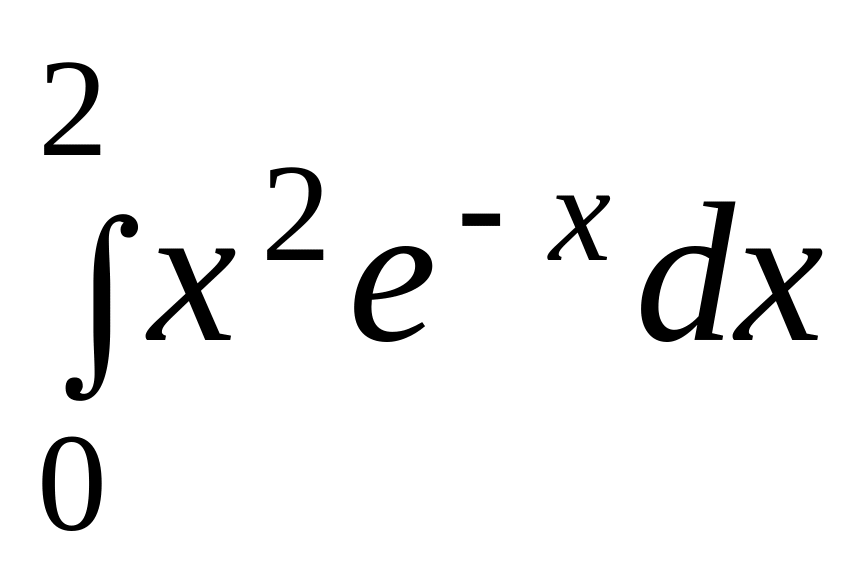 .
.а)
 ;
б)
;
б)
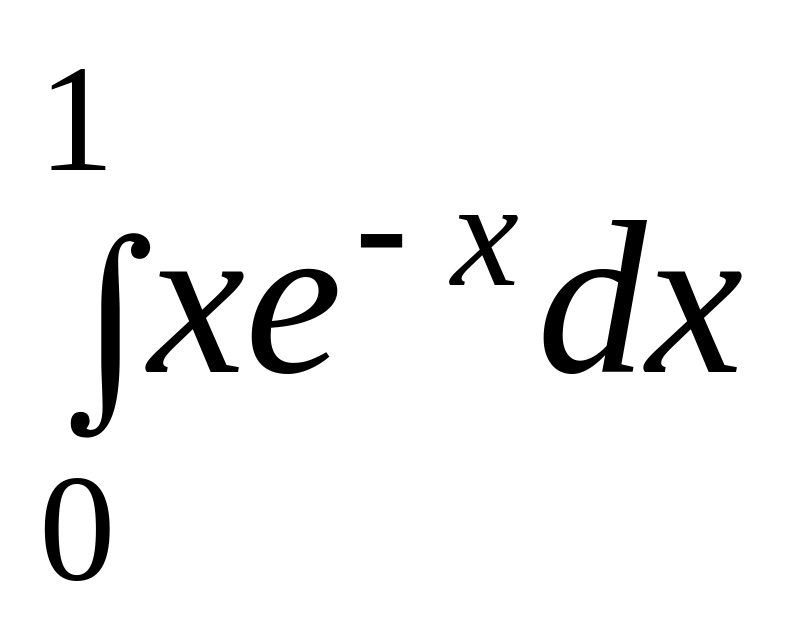 .
.
а)
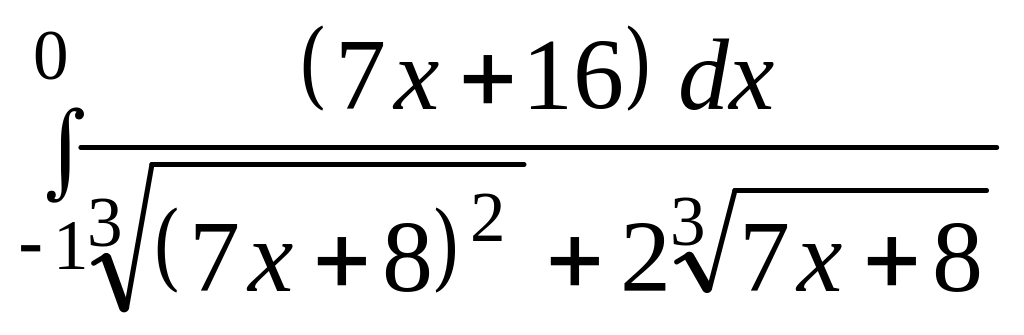 ;
б)
;
б)
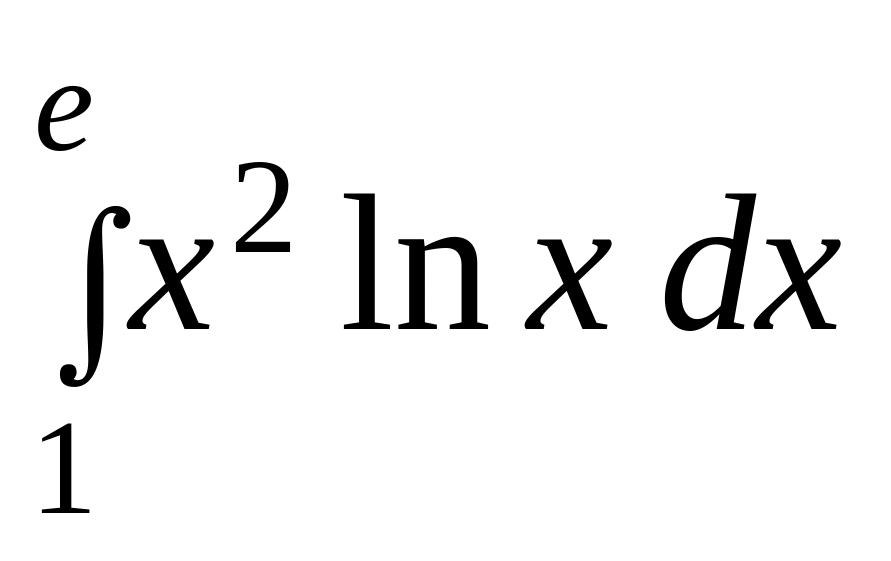 .
.а)
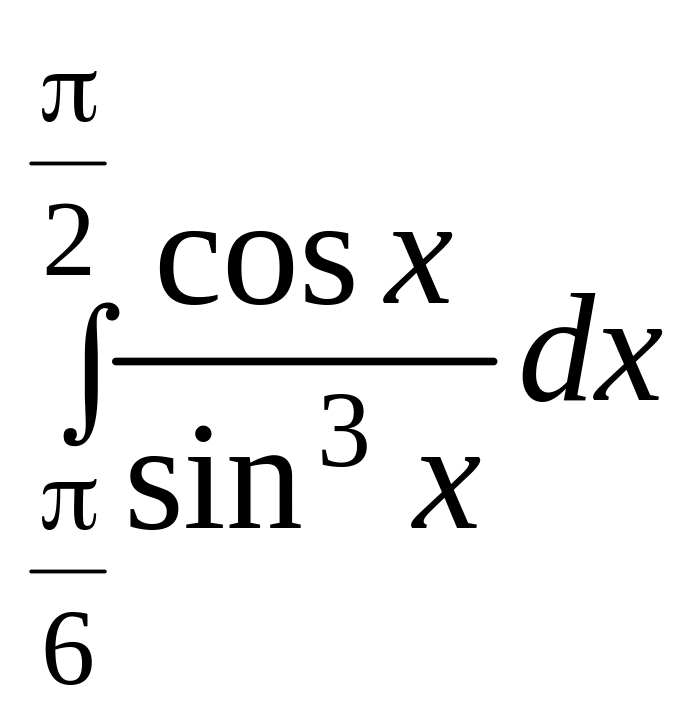 ;
б)
;
б)
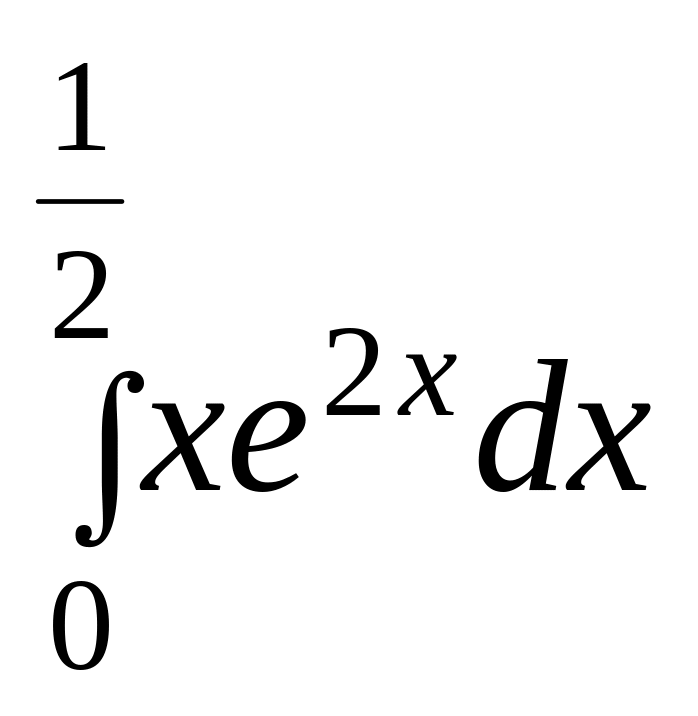 .
.а)
 ;
б)
;
б)
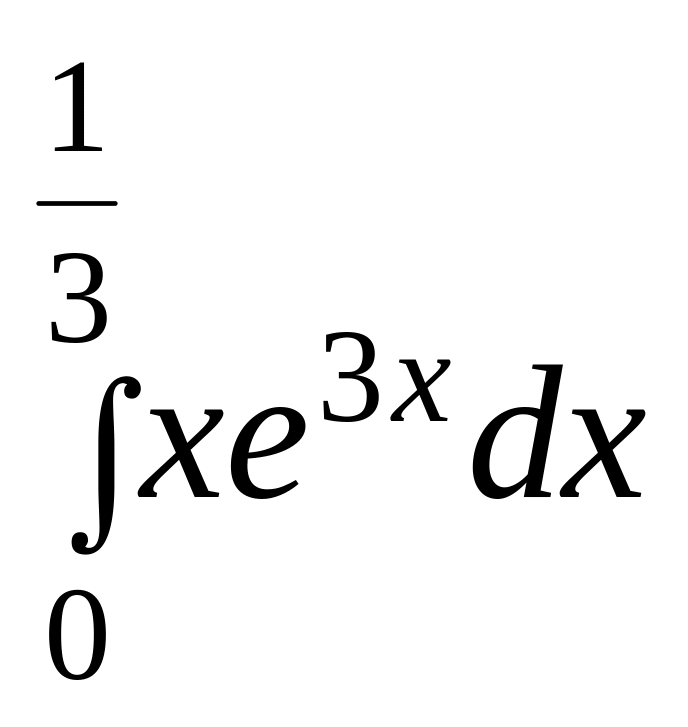 .
.а)
 ;
б)
;
б)
 .
.а)
 ;
б)
;
б)
 .
.а)
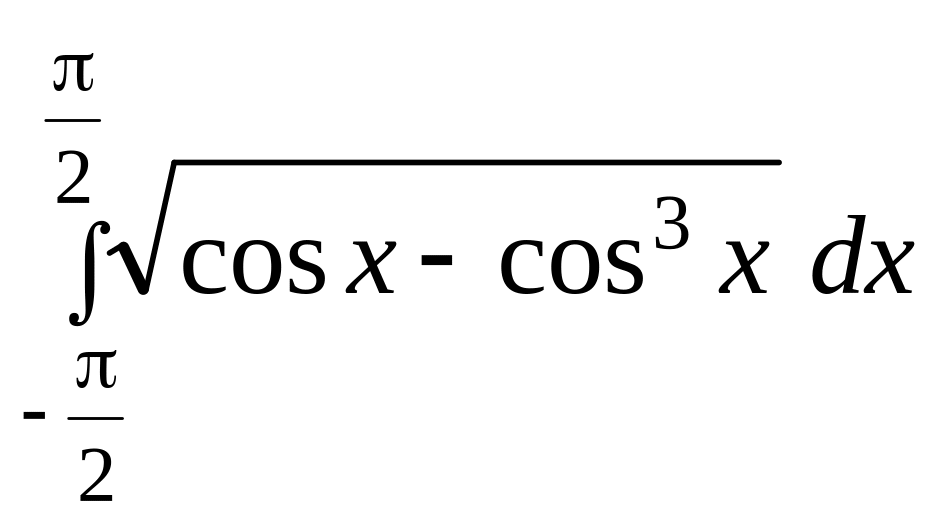 ;
б)
;
б)
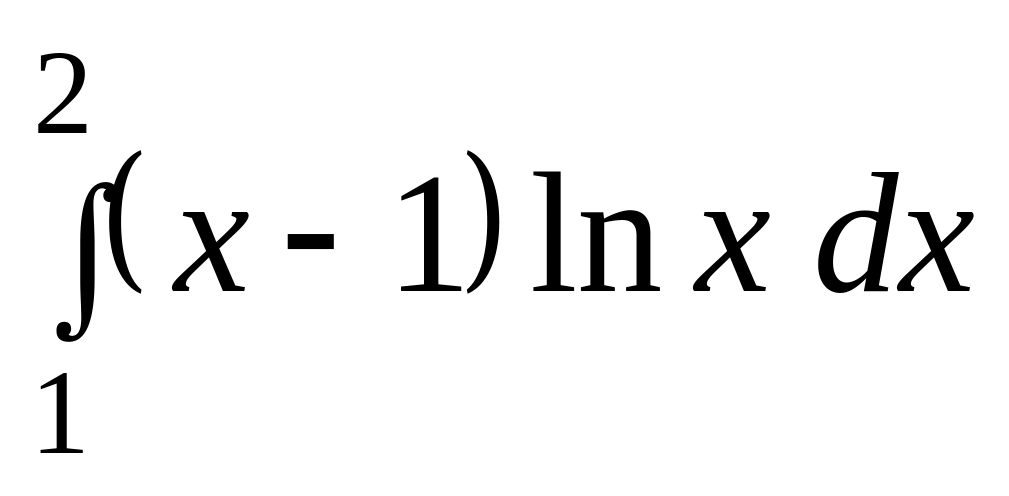 .
.а)
 ;
б)
;
б)
 .
.
Задание 3. Вычислить несобственный интеграл или установить расходимость.
а)
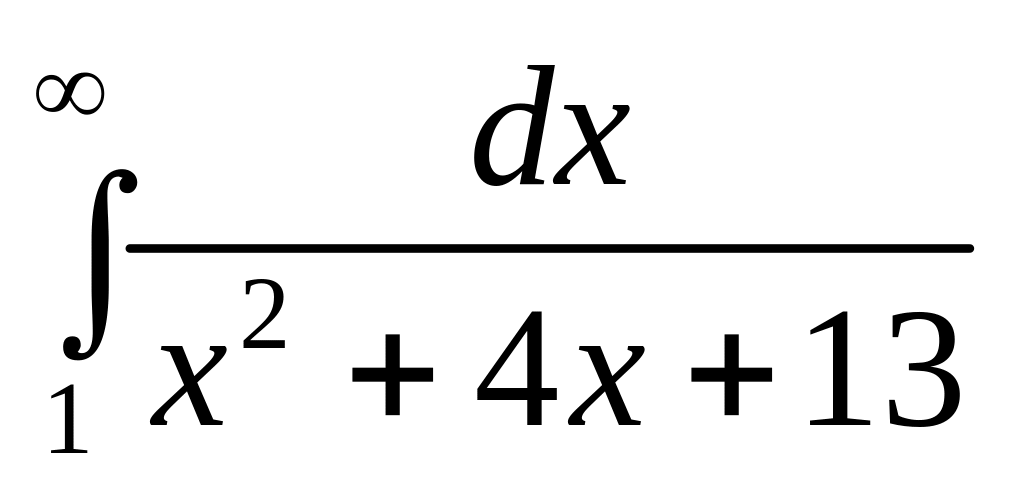 ;
б)
;
б)
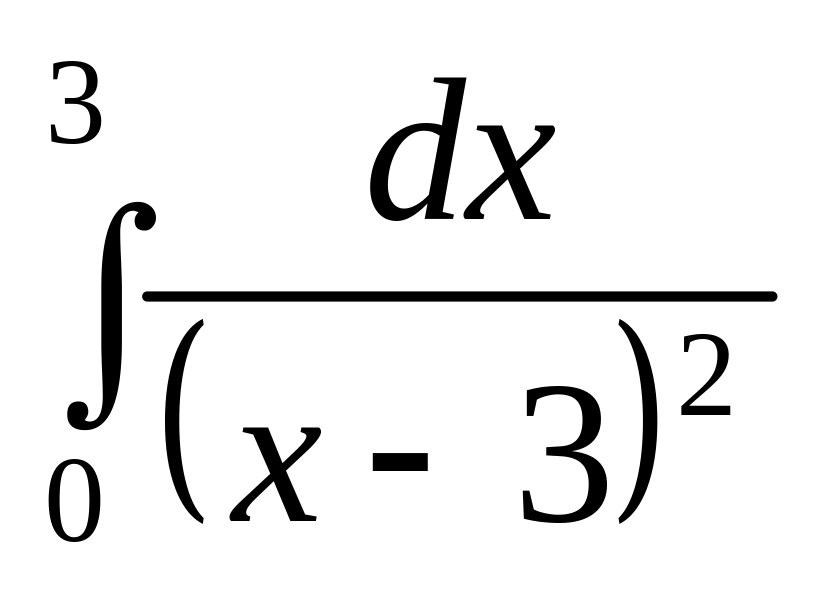 .
.а)
 ;
б)
;
б)
 .
.а)
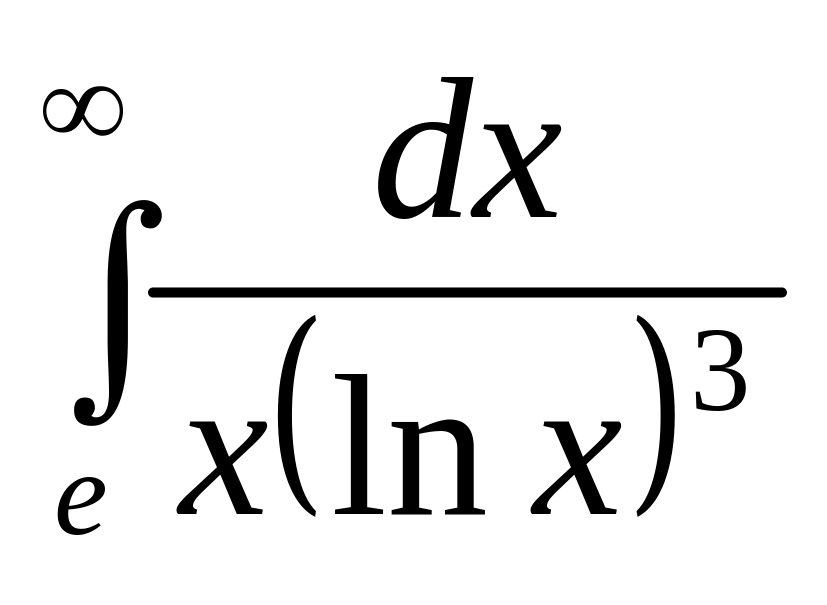 ;
б)
;
б)
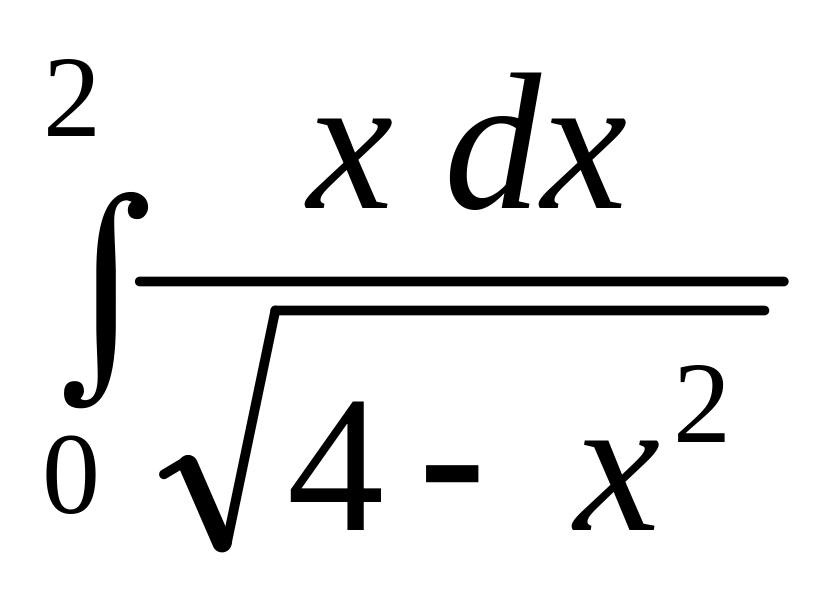 .
.а)
 ;
б)
;
б)
 .
.а)
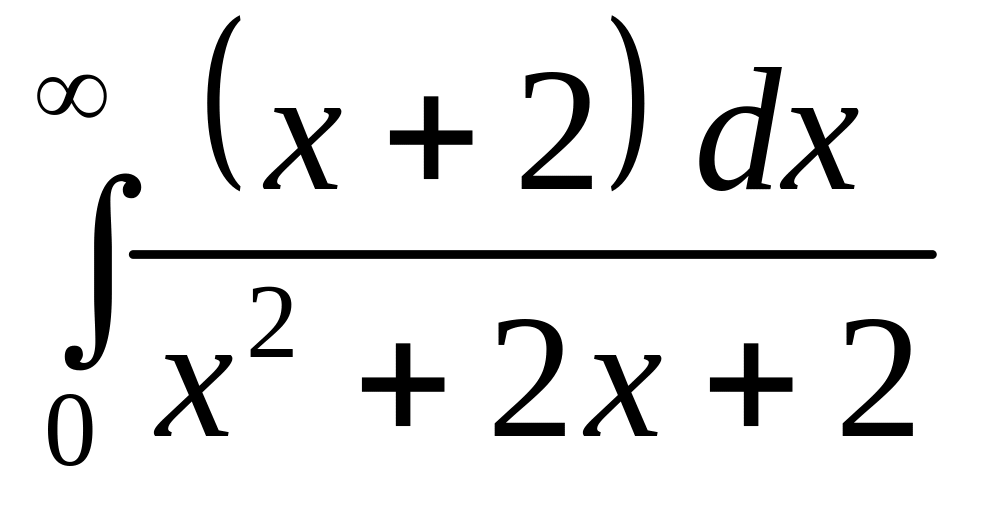 ;
б)
;
б)
 .
.а)
 ;
б)
;
б)
 .
.
а)
 ;
б)
;
б)
 .
.а)
 ;
б)
;
б)
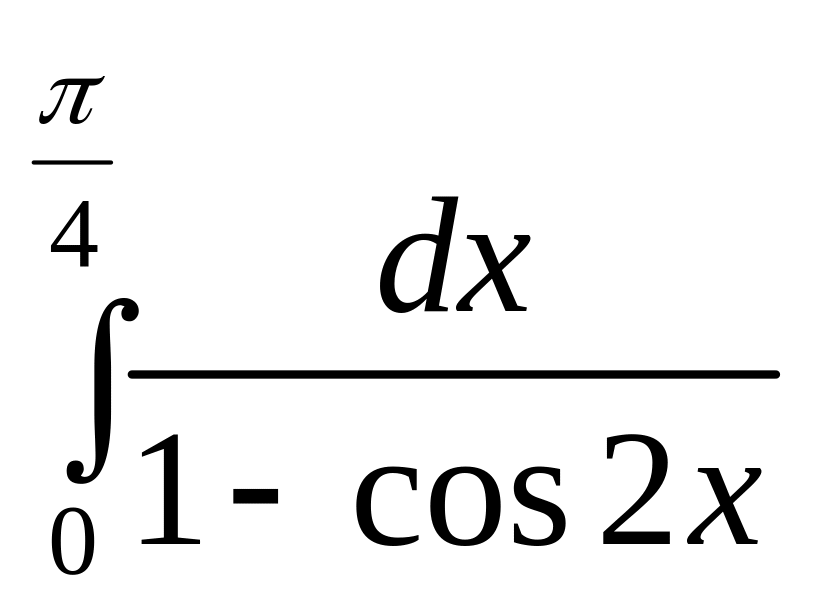 .
.а)
 ;
б)
;
б)
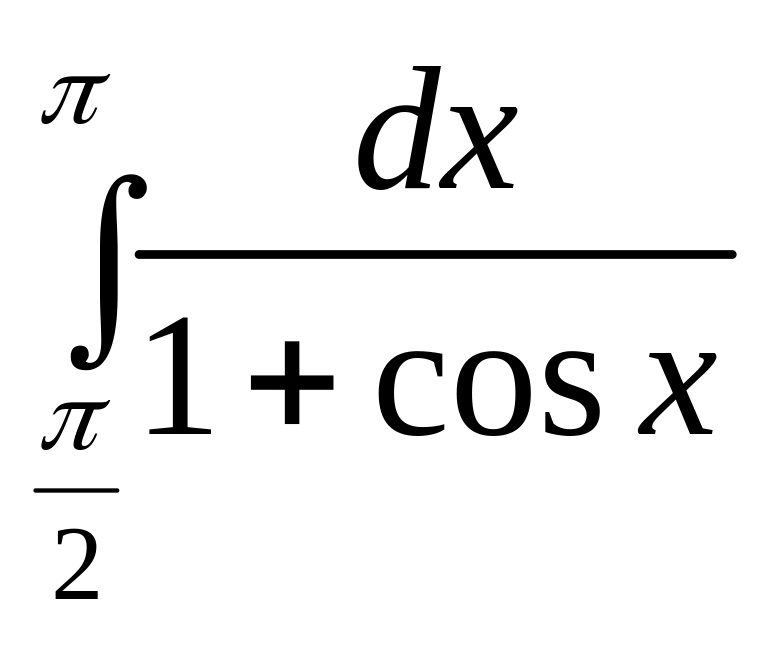 .
.а)
 ;
б)
;
б)
 .
.а)
 ;
б)
;
б)
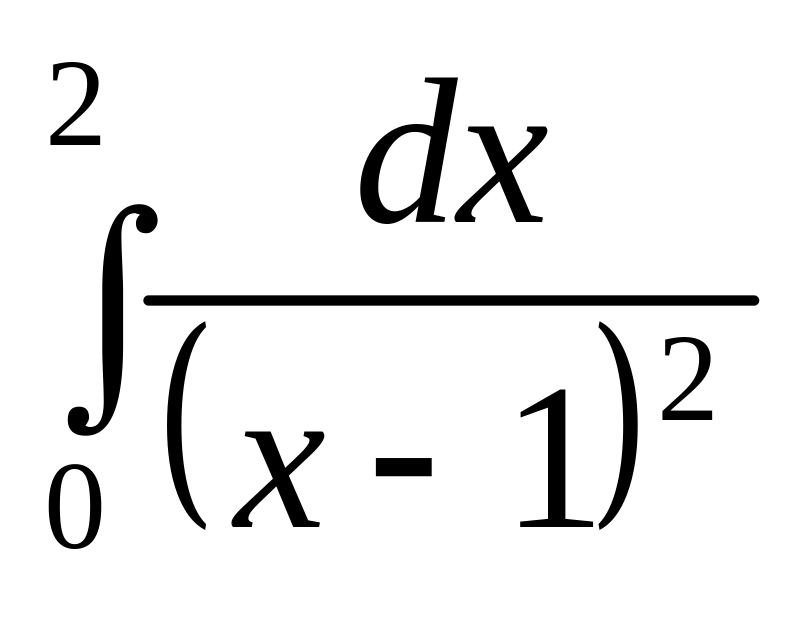 .
.а)
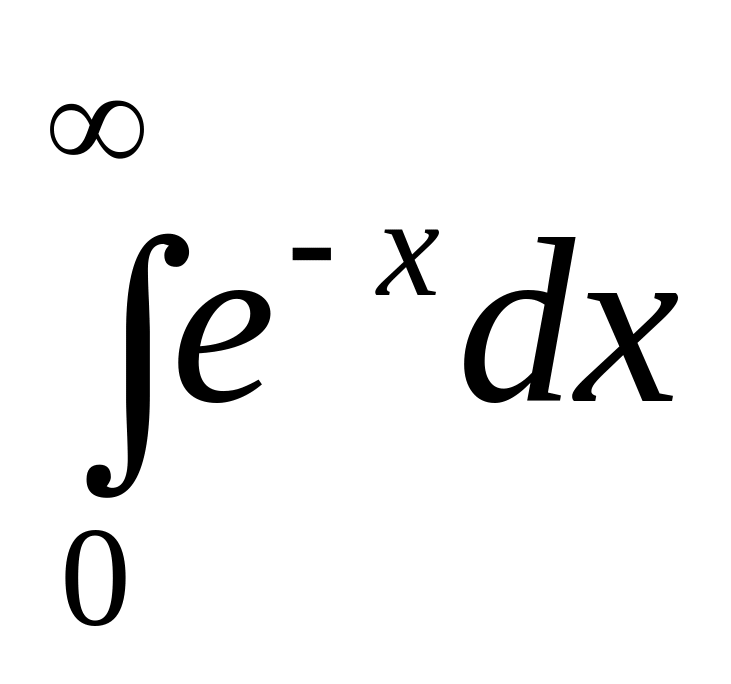 ;
б)
;
б)
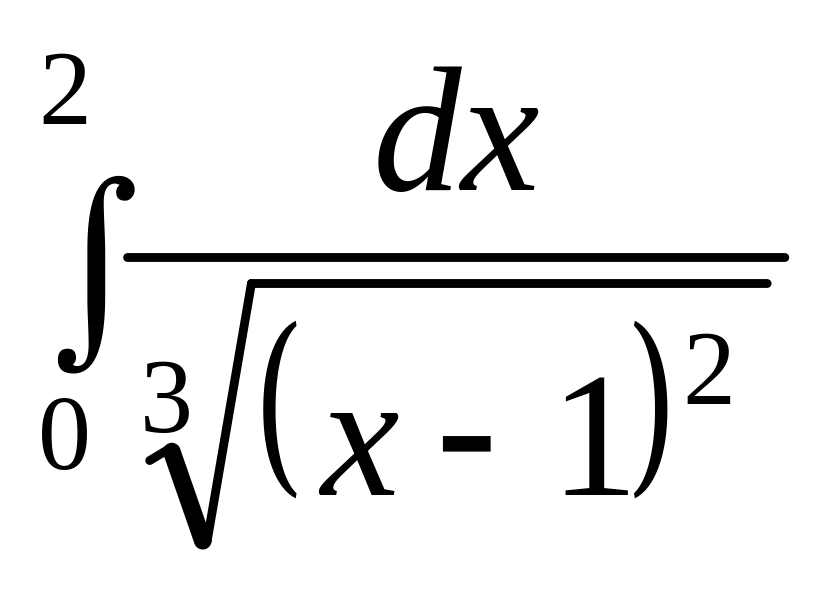 .
.а)
 ;
б)
;
б)
 .
.а)
 ;
б)
.
;
б)
.а)
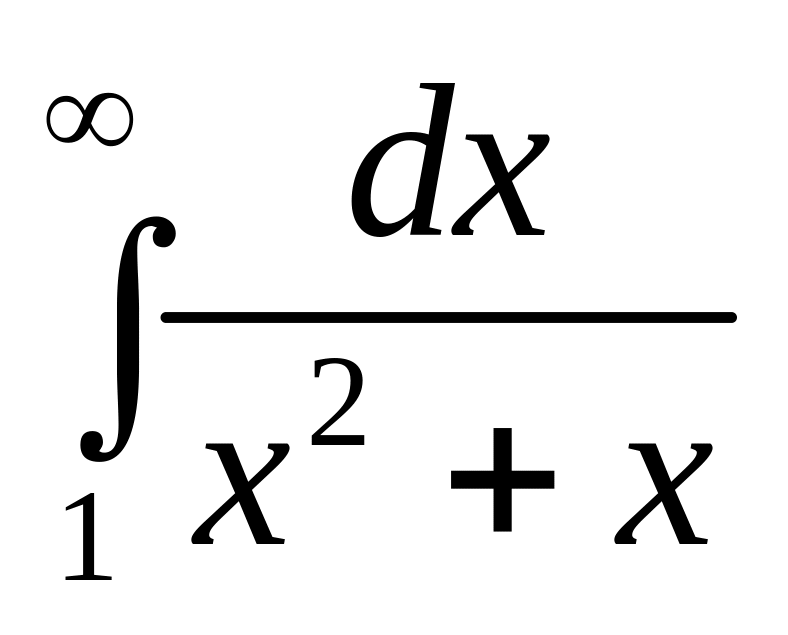 ;
б)
;
б)
 .
.а)
 ;
б)
;
б)
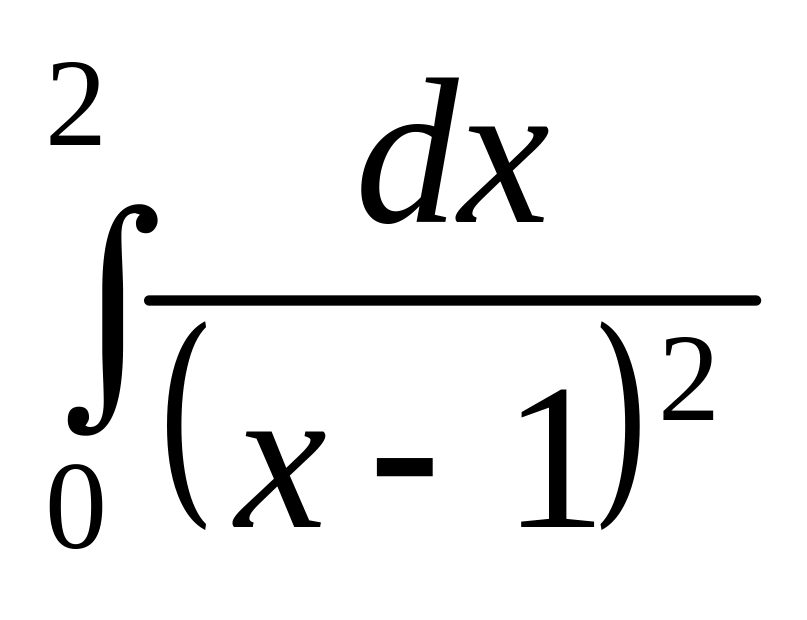 .
.а)
 ;
б)
;
б)
 .
.а)
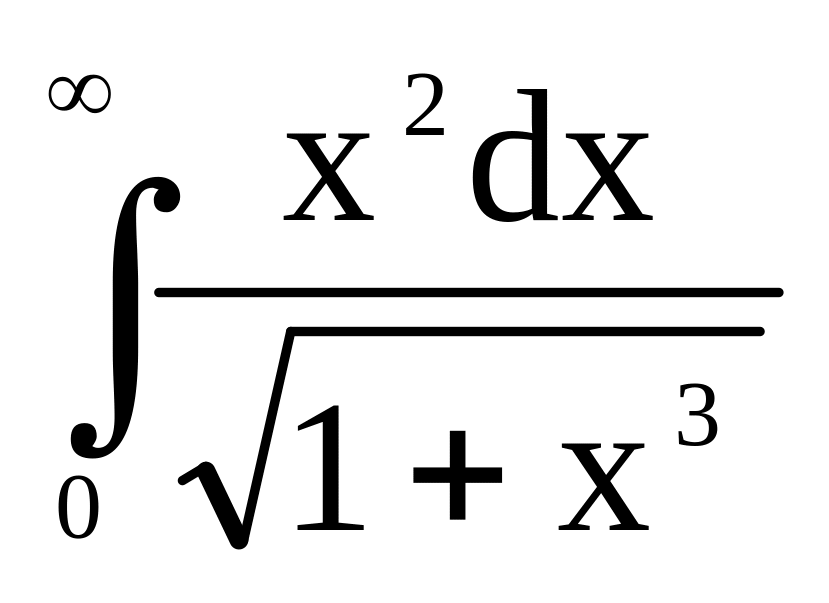 ;
б)
;
б)
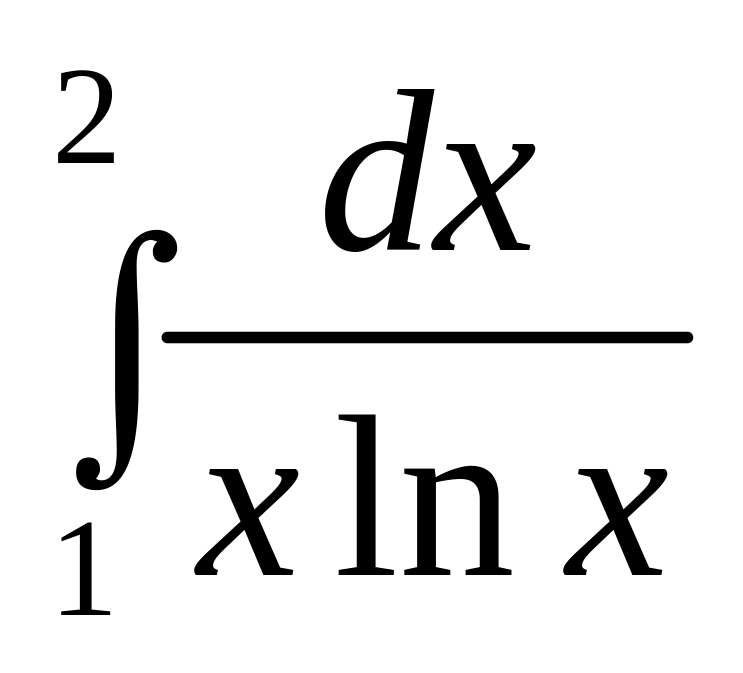 .
.а)
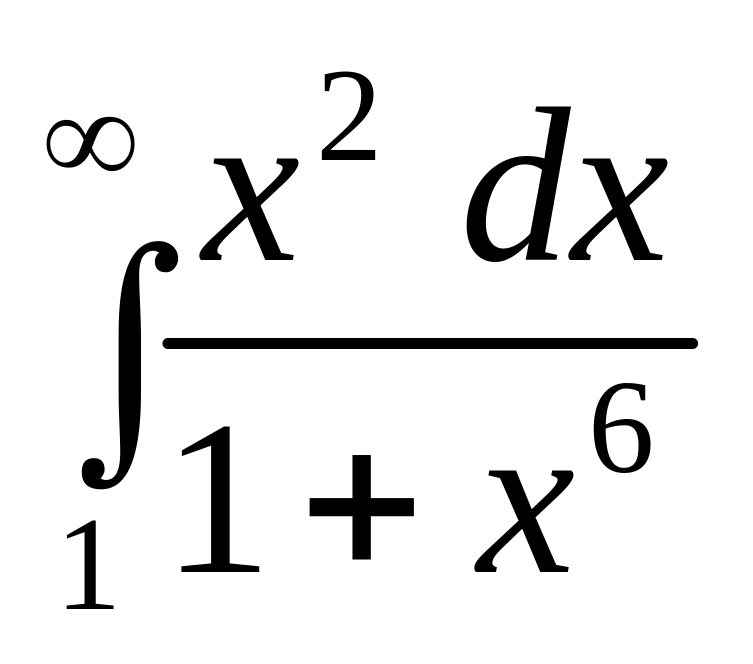 ;
б)
;
б)
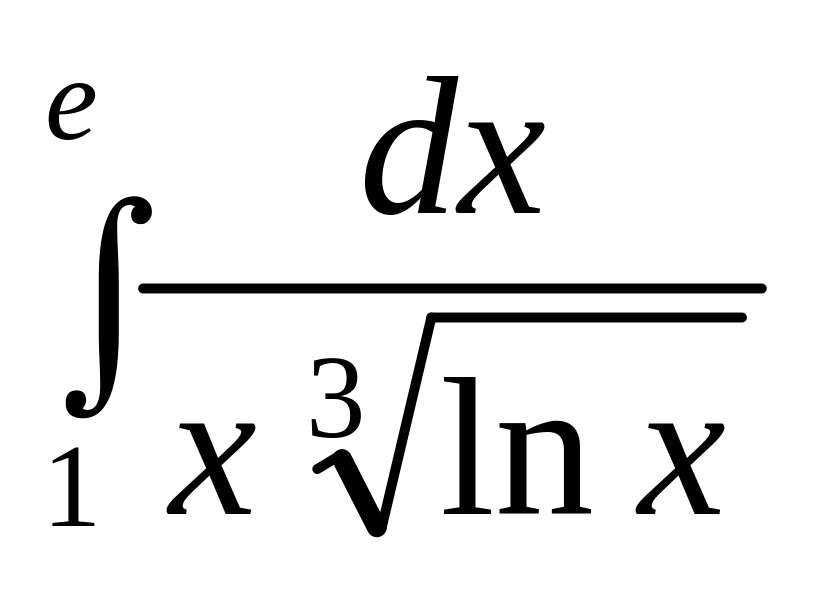 .
.а)
 ;
б)
;
б)
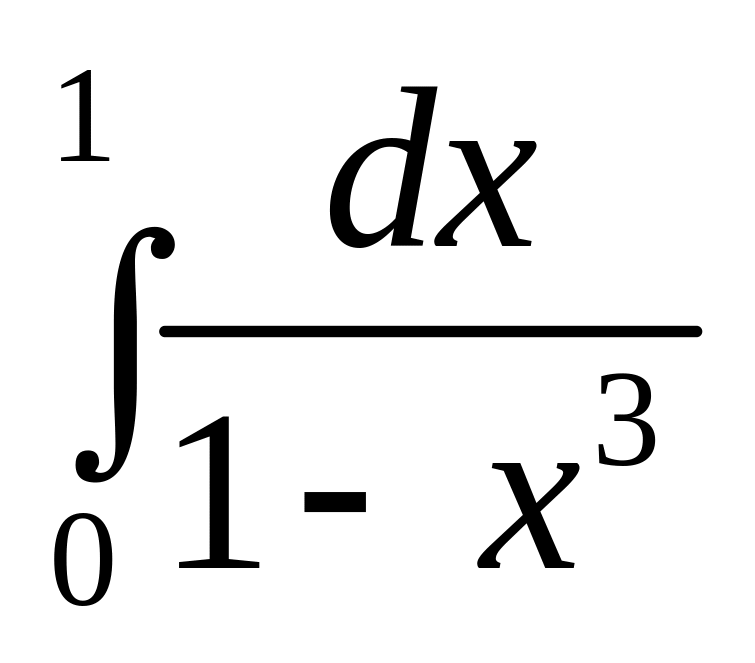 .
.а)
 ;
б)
;
б)
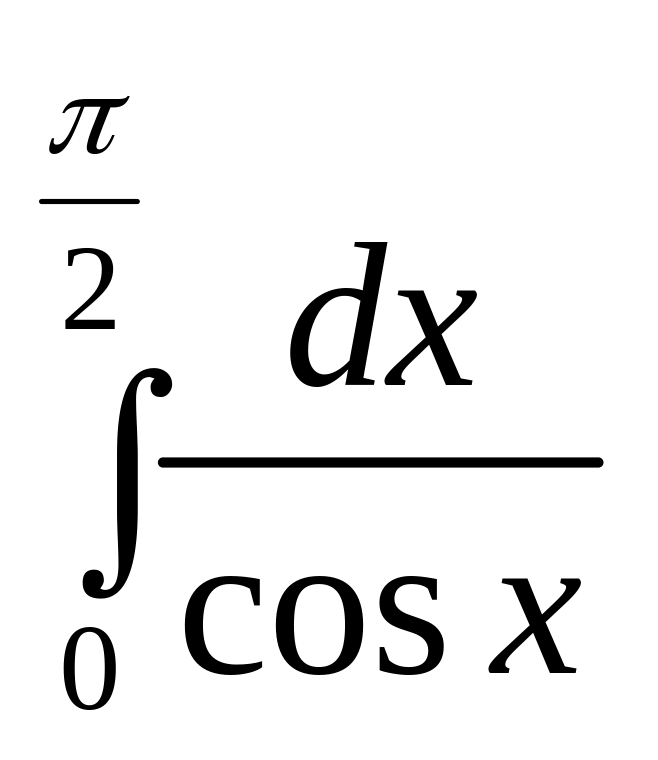 .
.а)
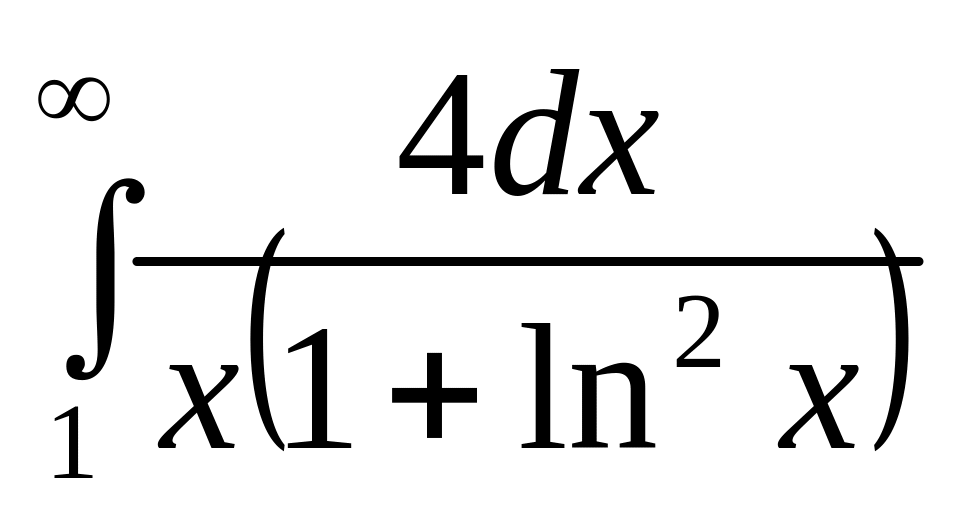 ;
б)
;
б)
 .
.а)
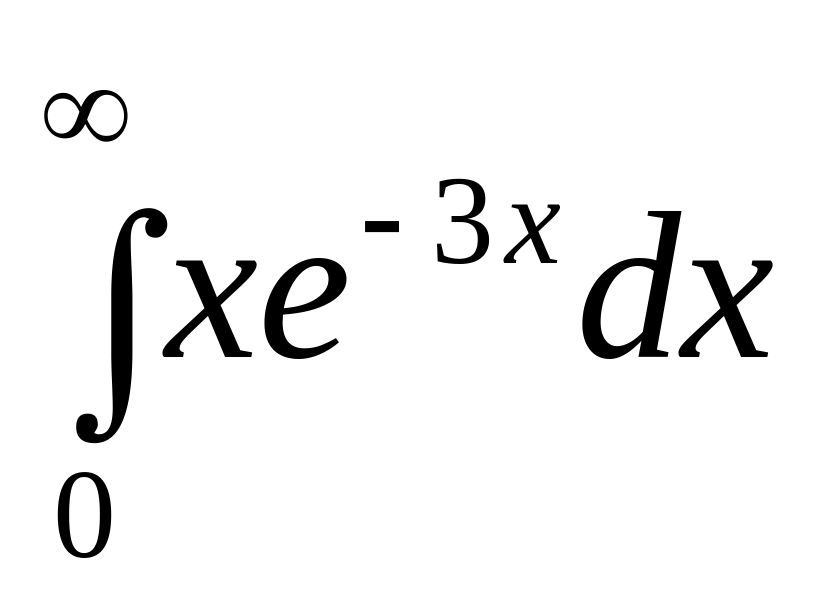 ;
б)
;
б)
 .
.а)
 ;
б)
;
б)
 .
.а)
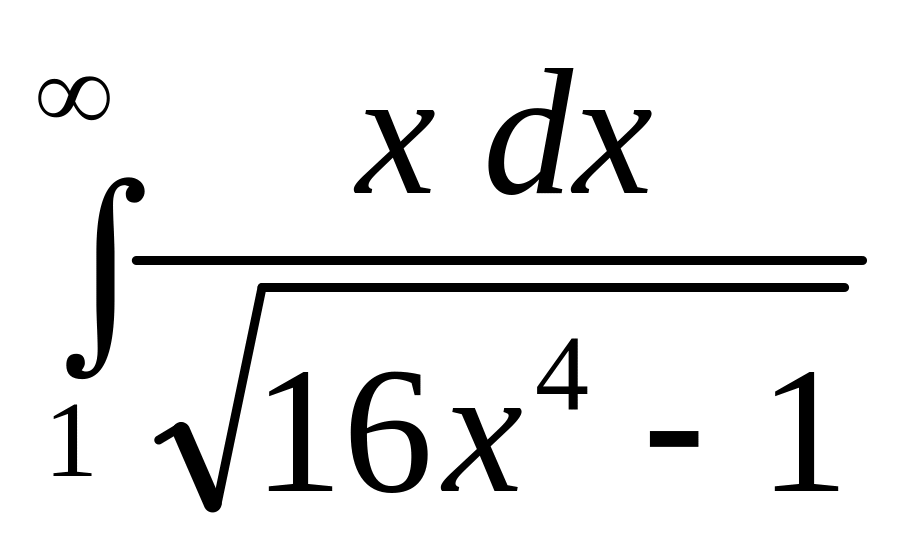 ;
б)
;
б)
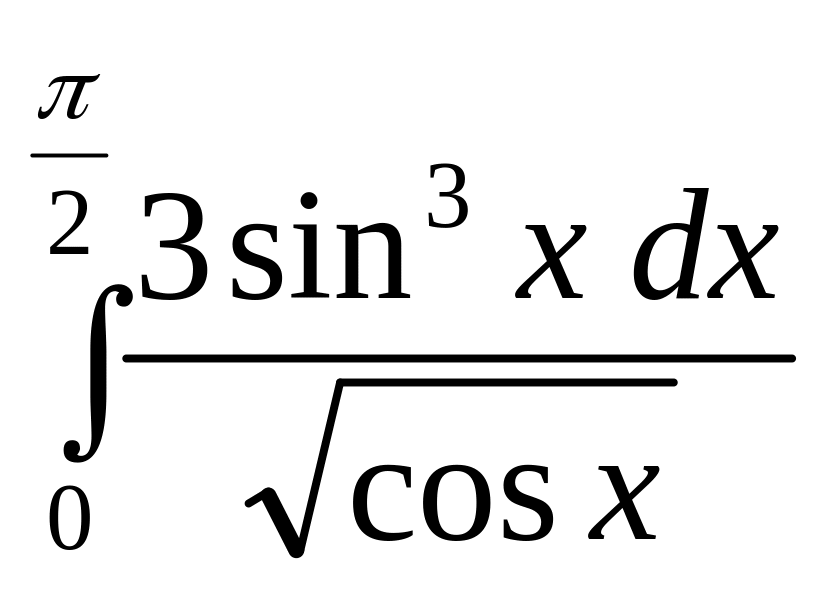 .
.а)
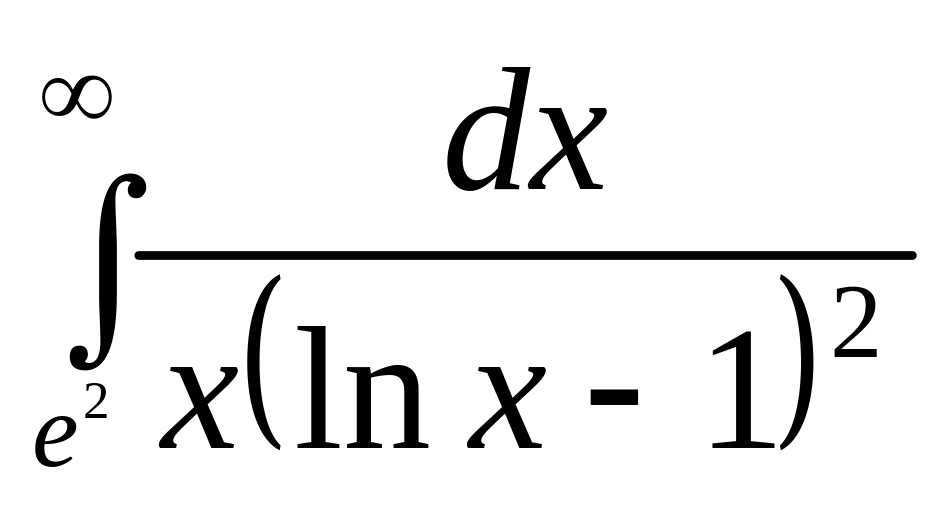 ;
б)
;
б)
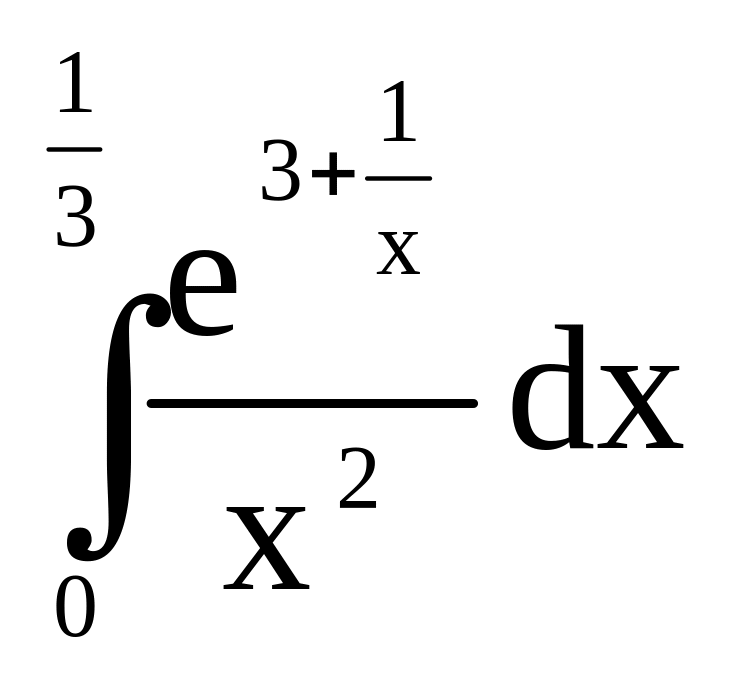 .
.а)
 ;
б)
;
б)
 .
.а)
 ;
б)
;
б)
 .
.а)
 ;
б)
;
б)
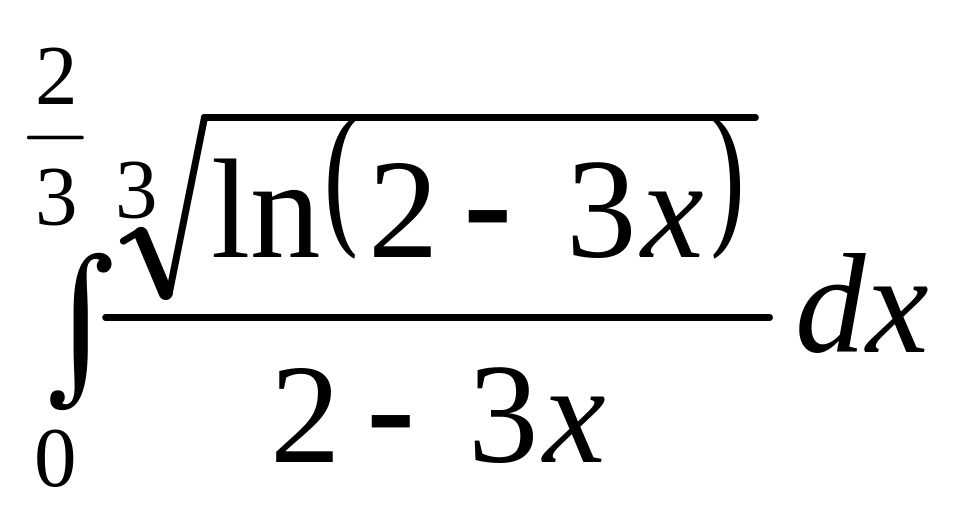 .
.а)
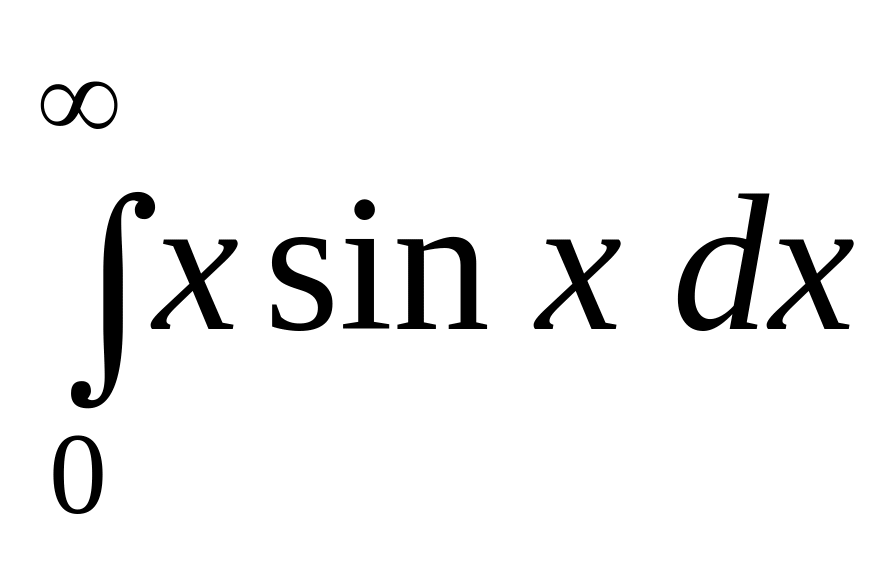 ;
б)
;
б)
 .
.
Задание 4. Вычислить площадь фигуры, ограниченной линиями.
 и
и
 .
.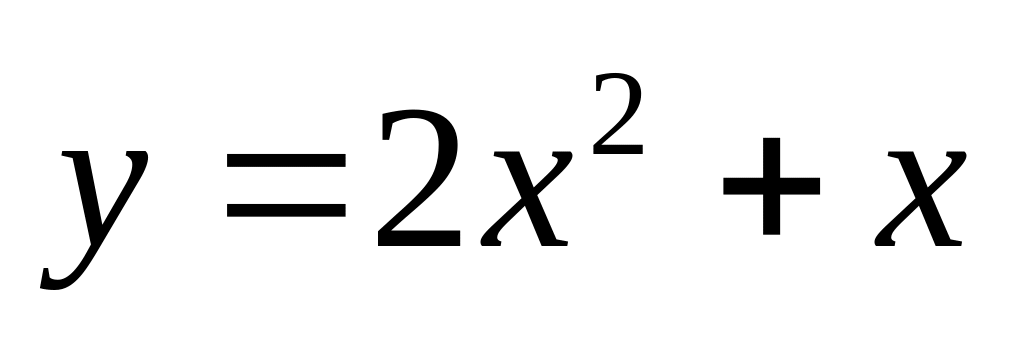 и
и
 .
. и
и
 .
. и
и
 .
. и
и
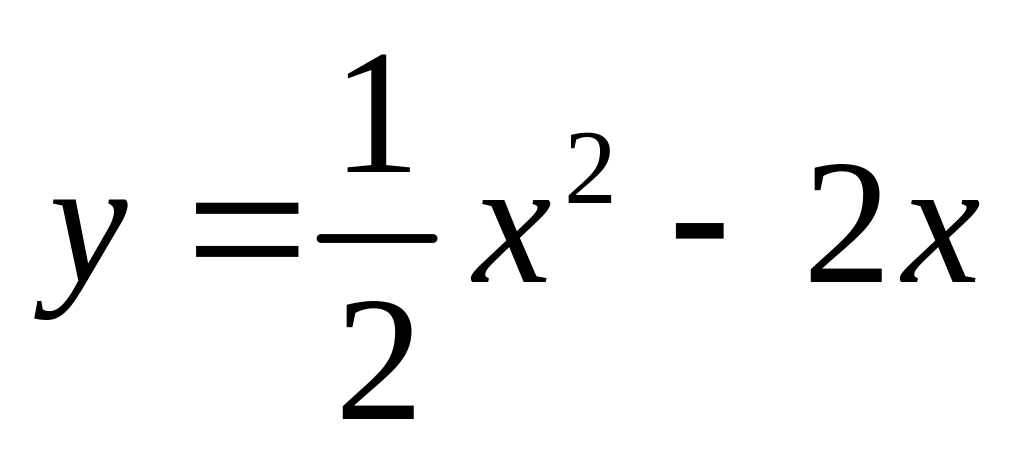 .
.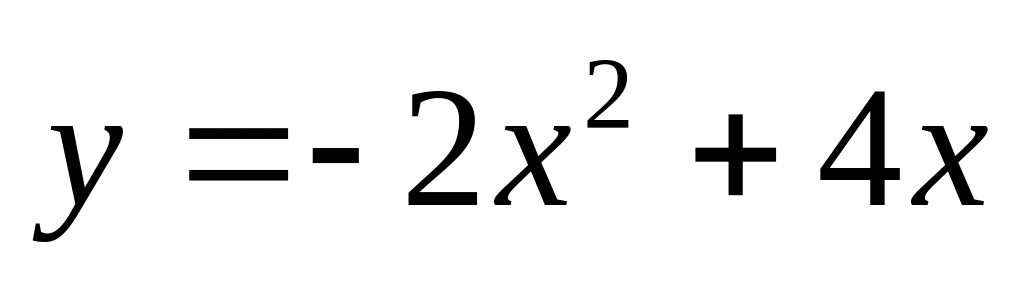 и
и
 .
. и
и
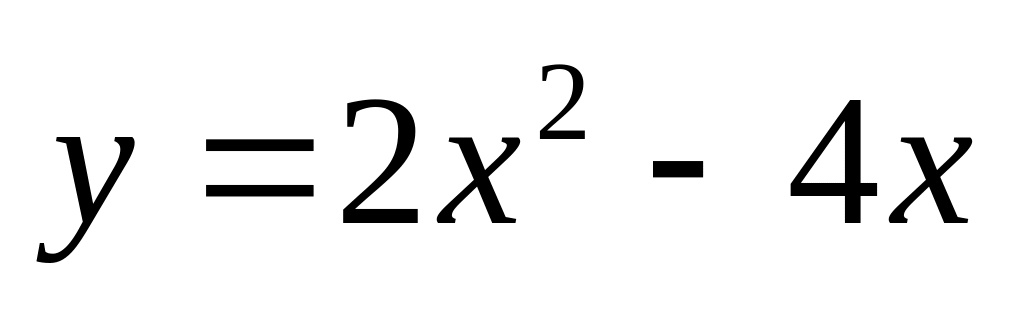 .
.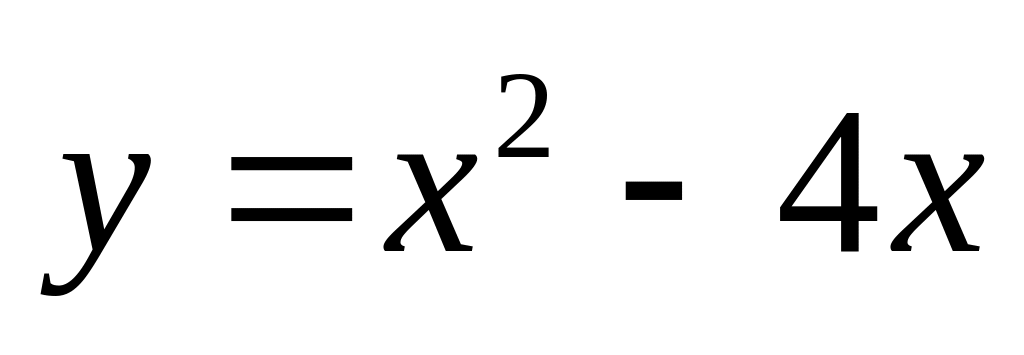 и
и
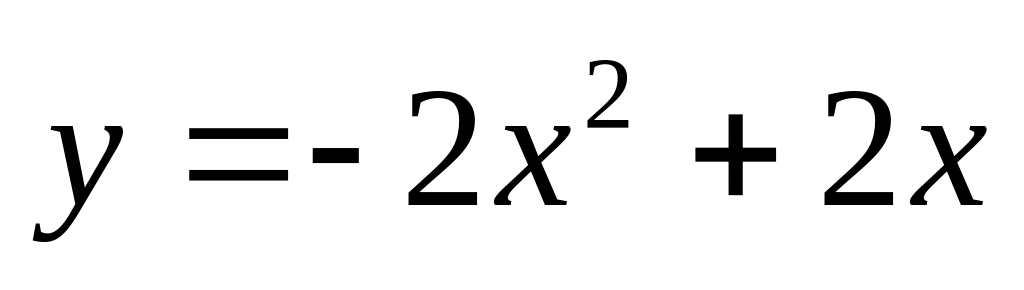 .
. и
и
 .
. и
и
 .
.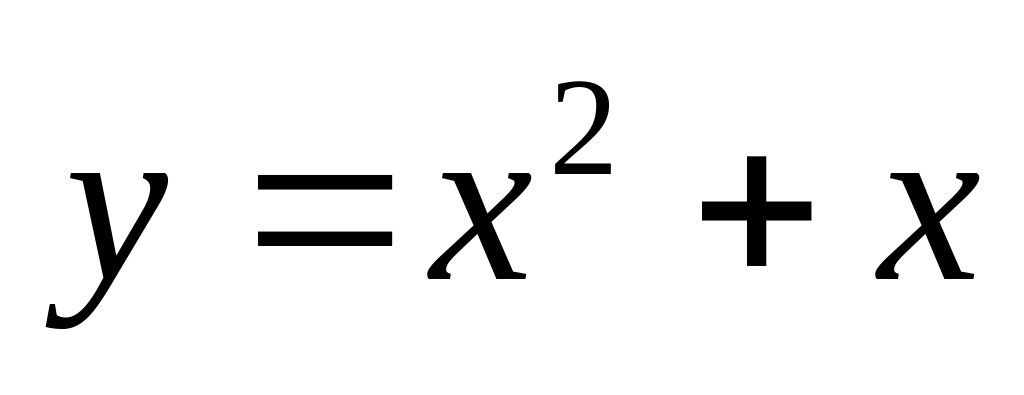 и
и
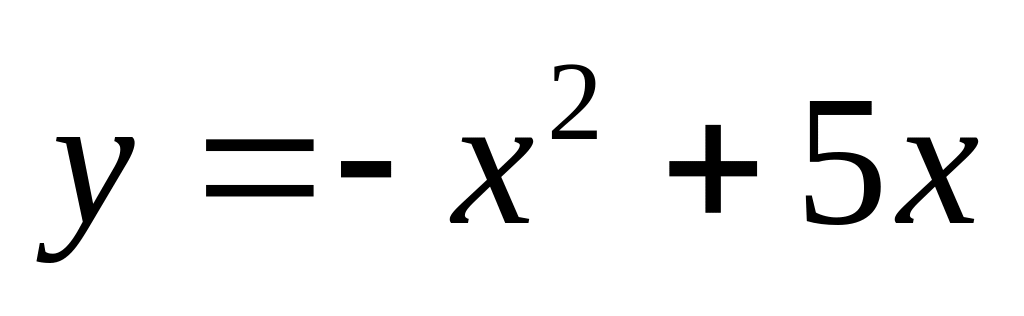 .
.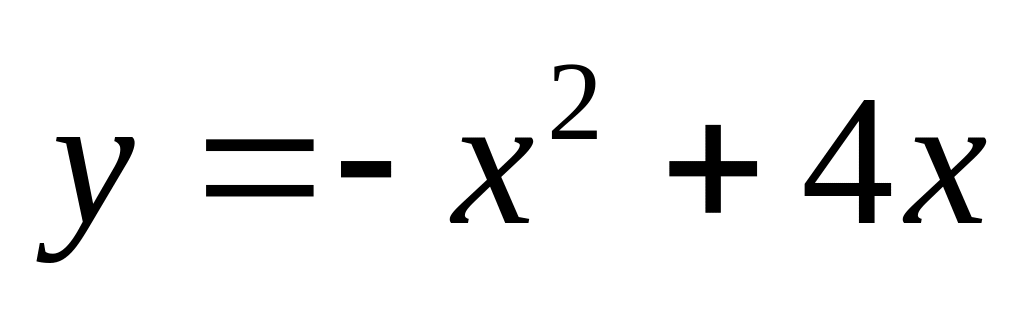 и
и
 .
.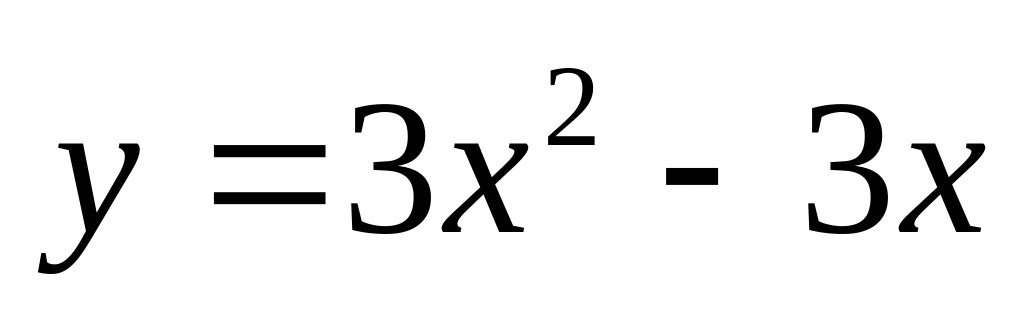 и
.
и
.и
 .
. и
и
 .
. и
и
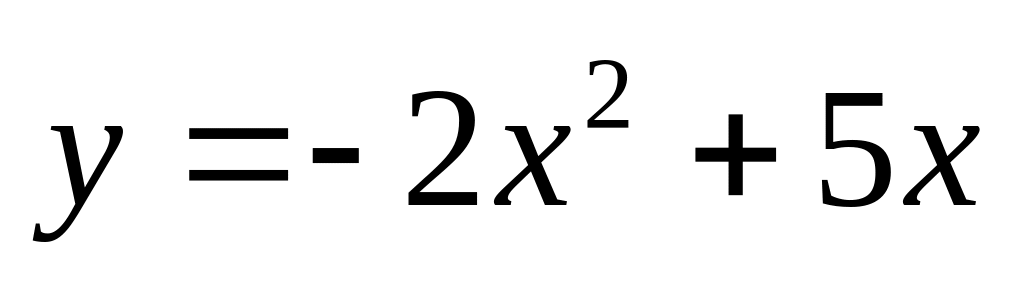 .
. и
и
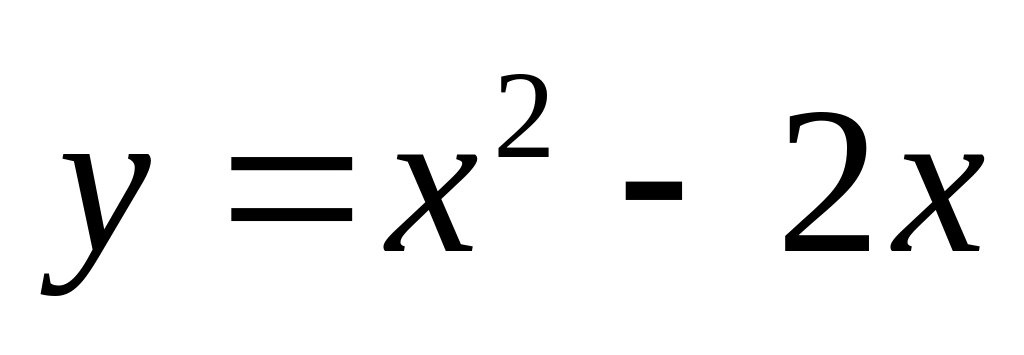 .
.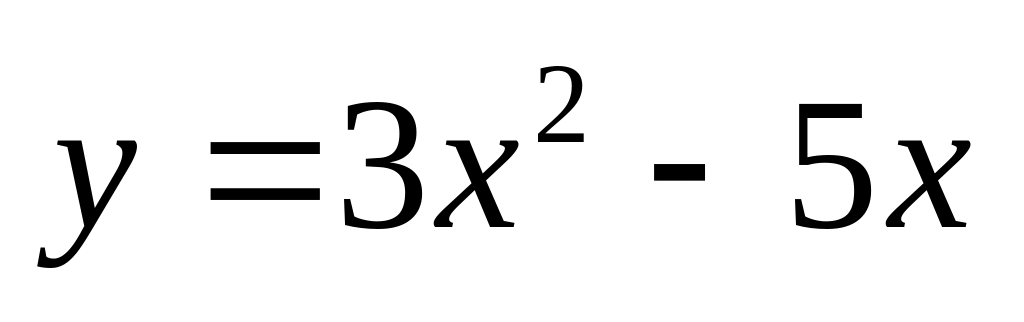 и
и
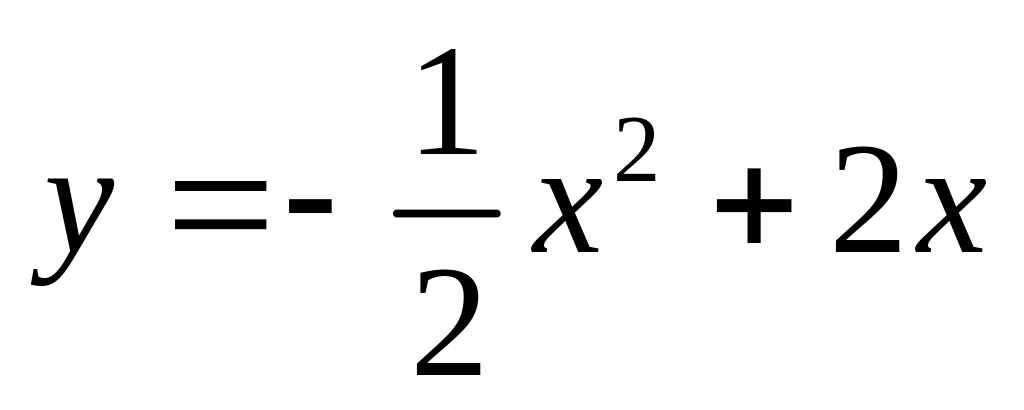 .
.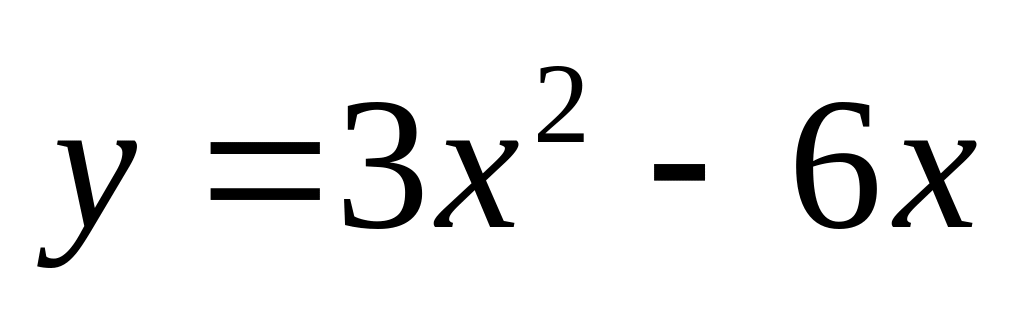 и
и
 .
.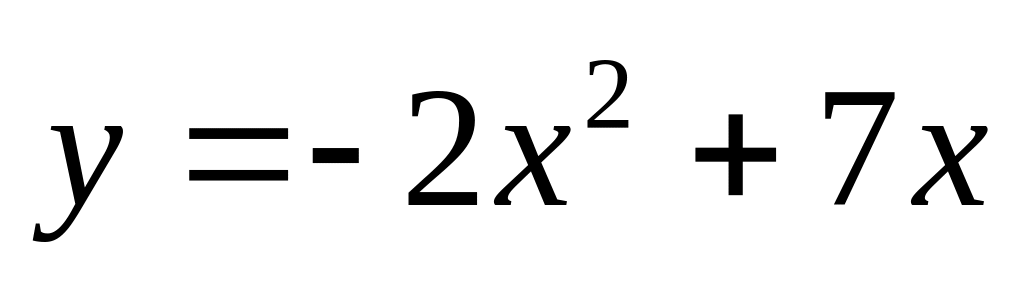 и
.
и
. и
и
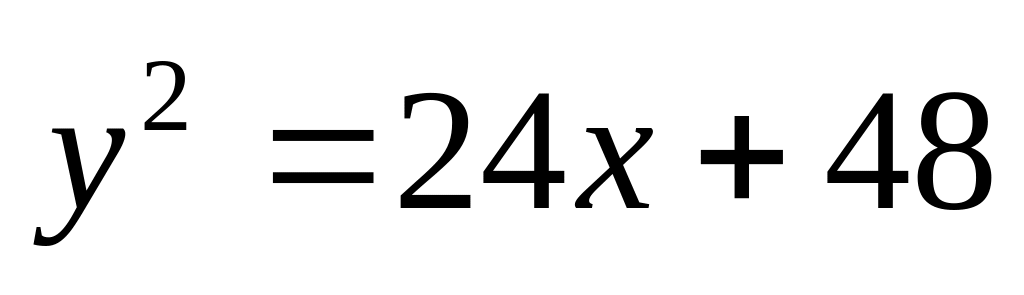 .
.и
 .
.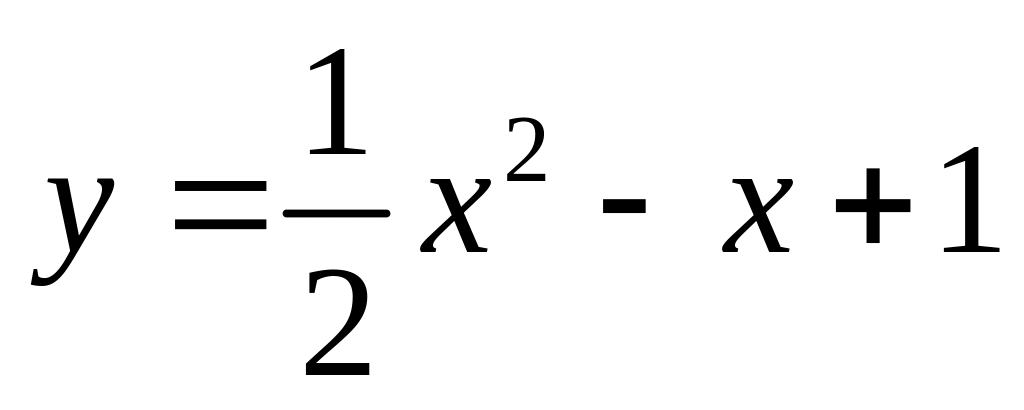 и
и
 .
. и
и
 .
. и
и
 .
.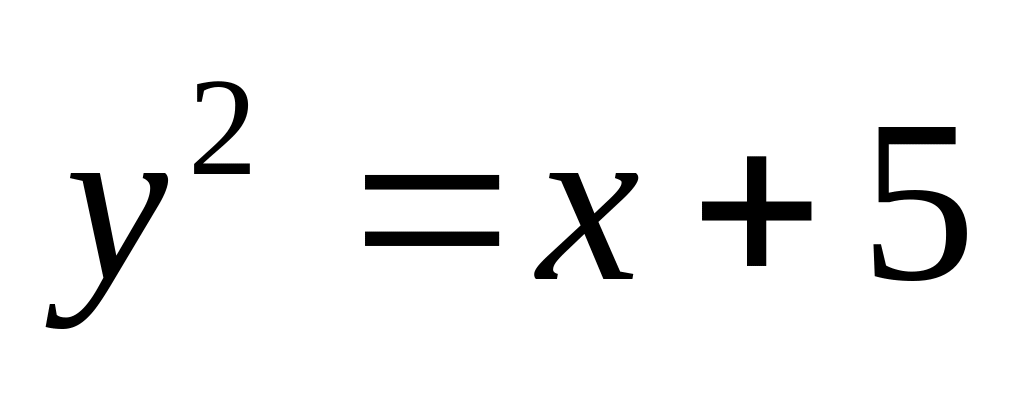 и
и
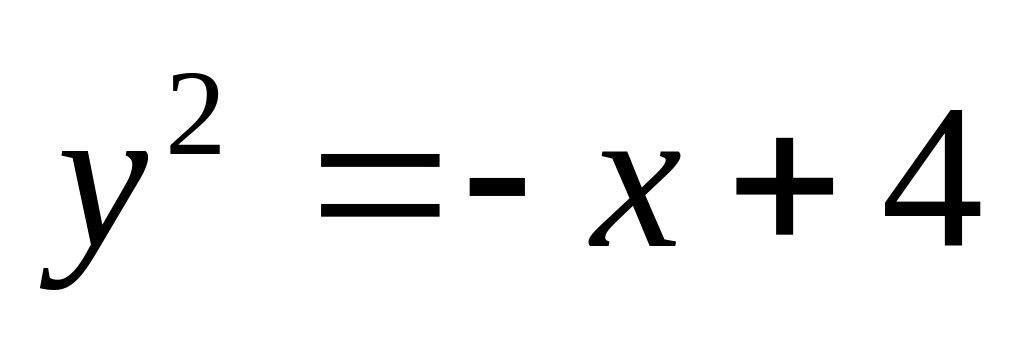 .
.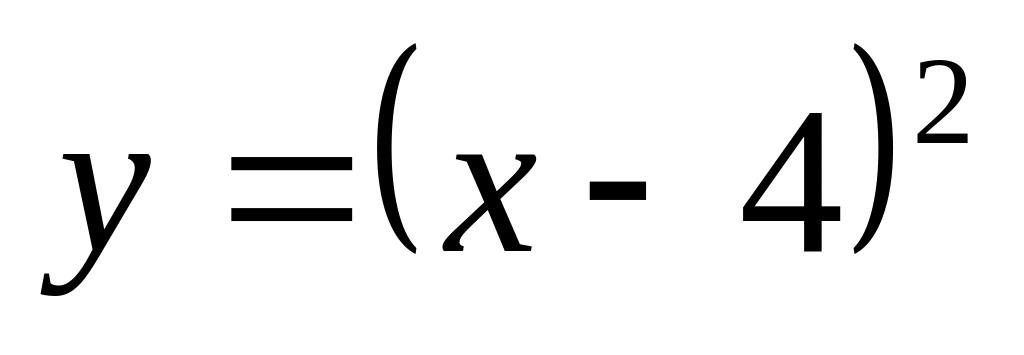 и
и
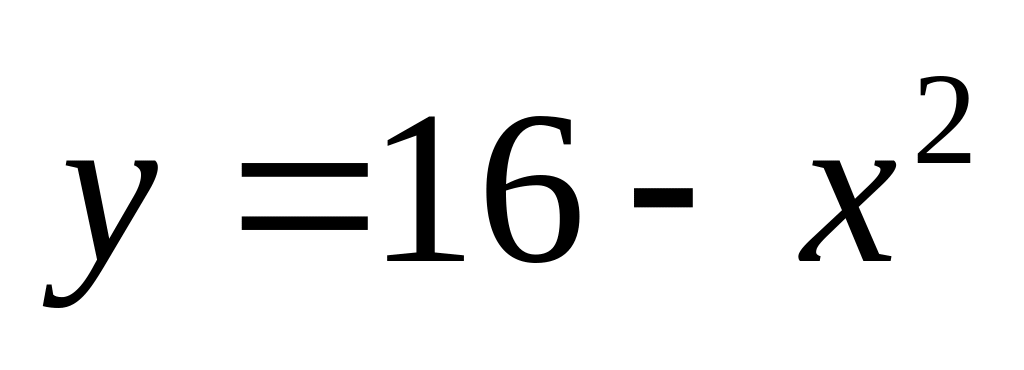 .
. и
и
 .
.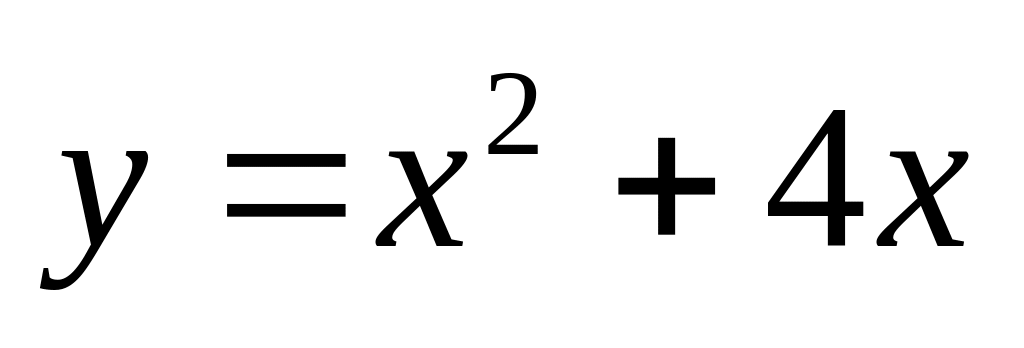 и
и
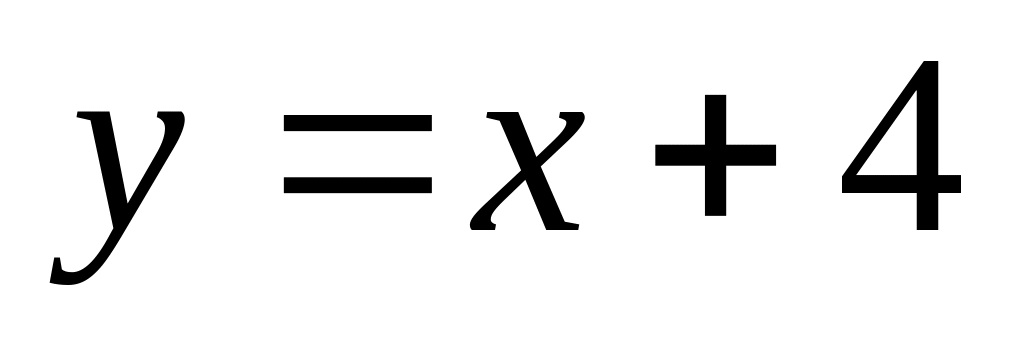 .
.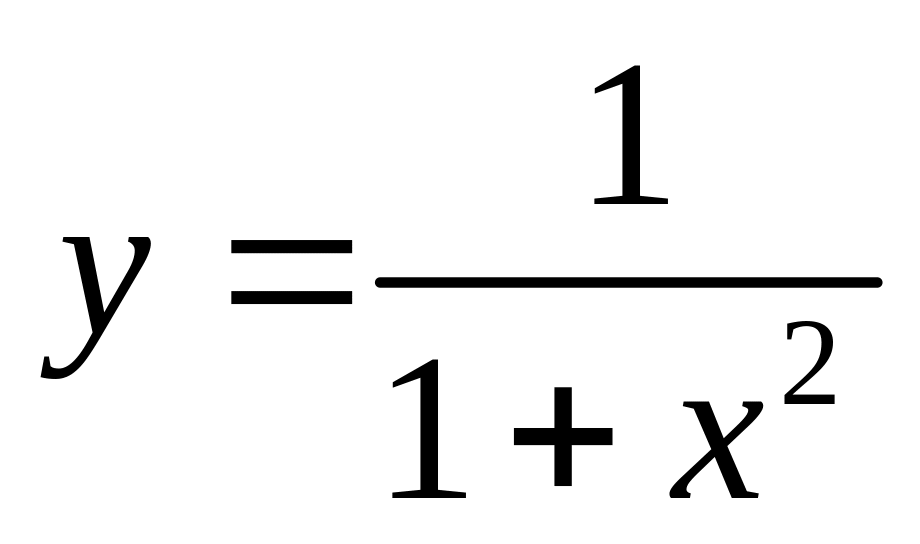 и
и
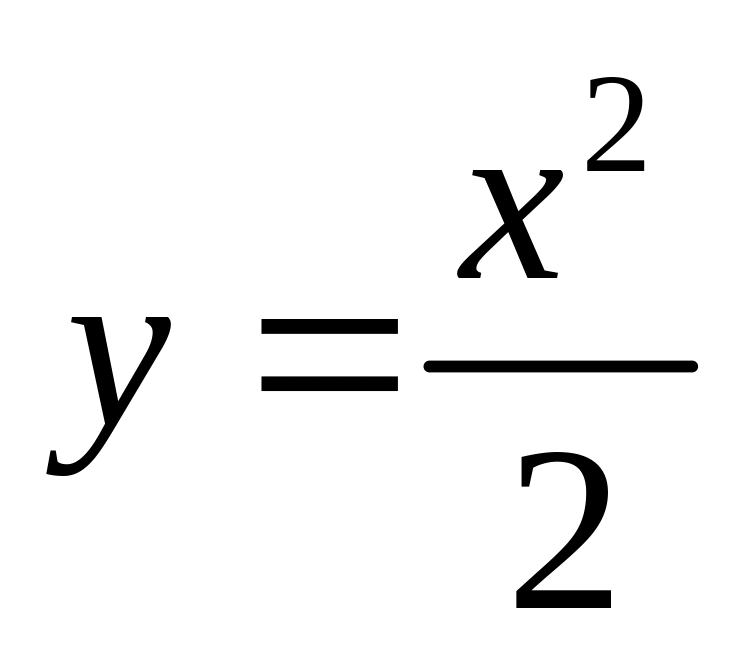 .
.
Задание 5. Вычислить длину дуги кривой.
Кардиоиды
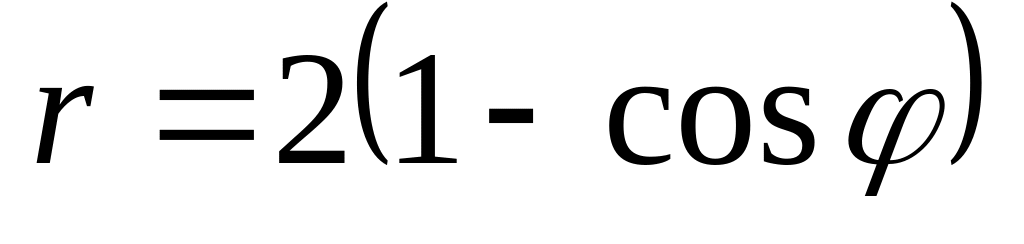 .
.Астроиды
 ,
,
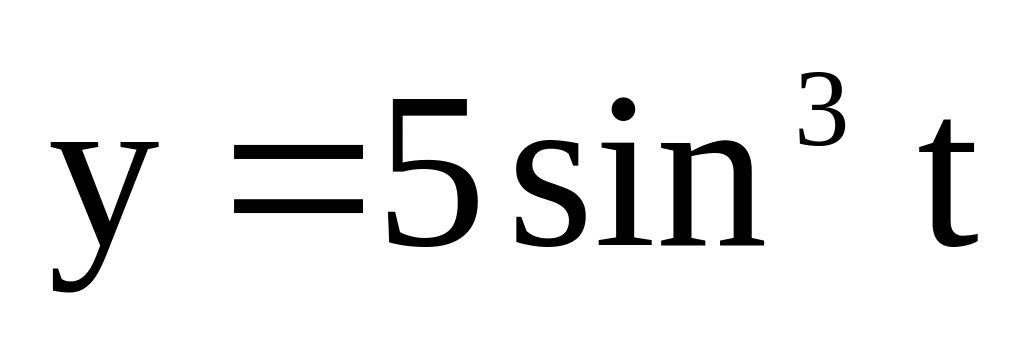 .
.Логарифмической спирали
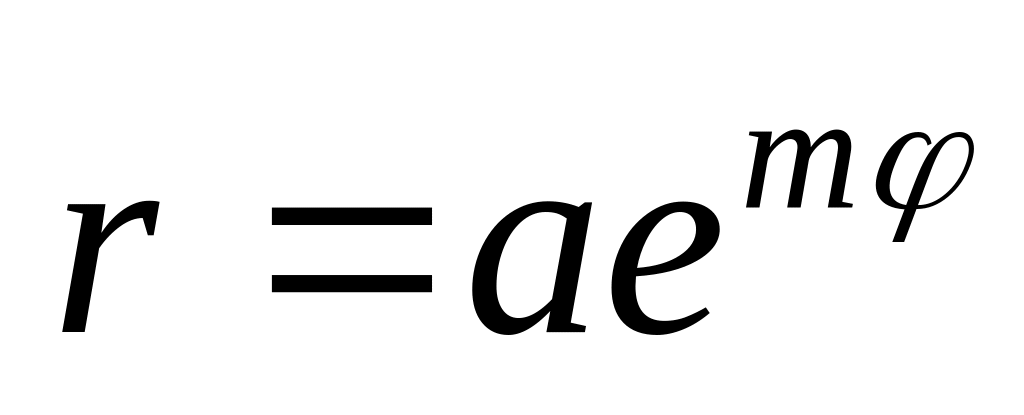 ,
,
 ,
находящейся внутри круга
,
находящейся внутри круга
 .
.Эволюты окружности
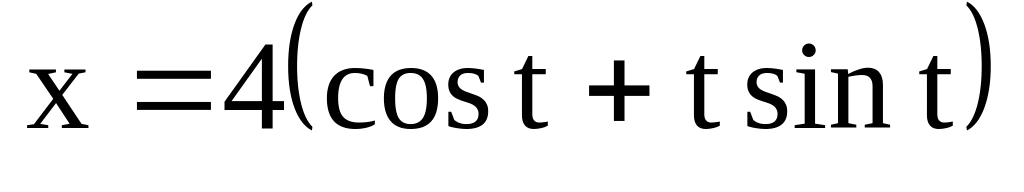 ,
,

при изменении
от 0 до
![]() .
.
Полукубической параболы
 от начала координат до точки
от начала координат до точки
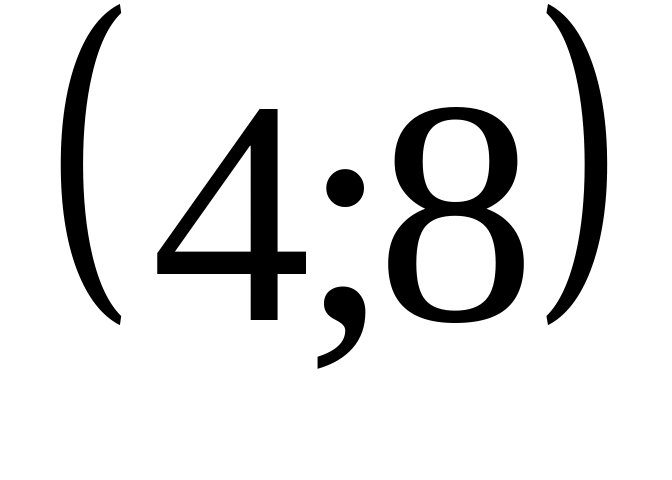 .
. при изменении
от 0 до
.
при изменении
от 0 до
.Первого витка спирали Архимеда
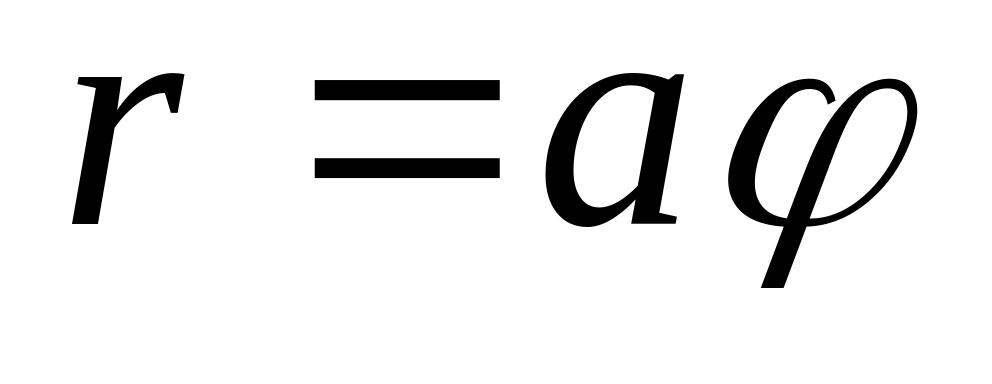 (
( ).
).Одной арки циклоиды
 ,
,
 .
.Астроиды
 ,
,
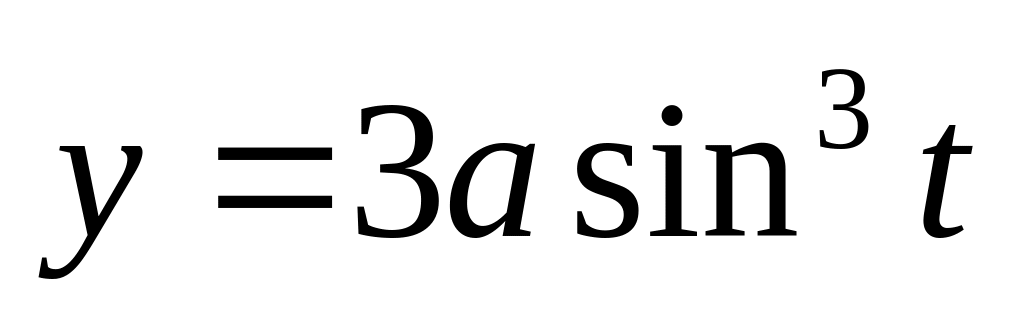 .
.Астроиды
 ,
,
 (
(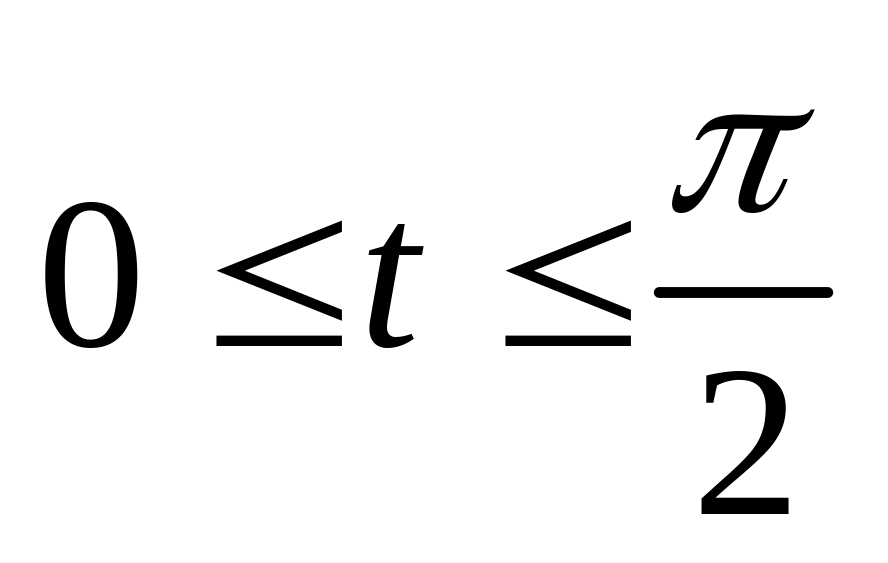 ).
).Полукубической параболы
 ,
где
,
где
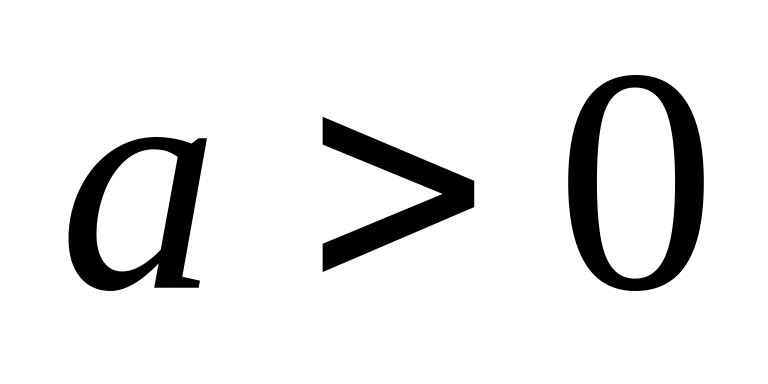 от точки с абсциссой
до точки с абсциссой
.
от точки с абсциссой
до точки с абсциссой
.Цепной линии
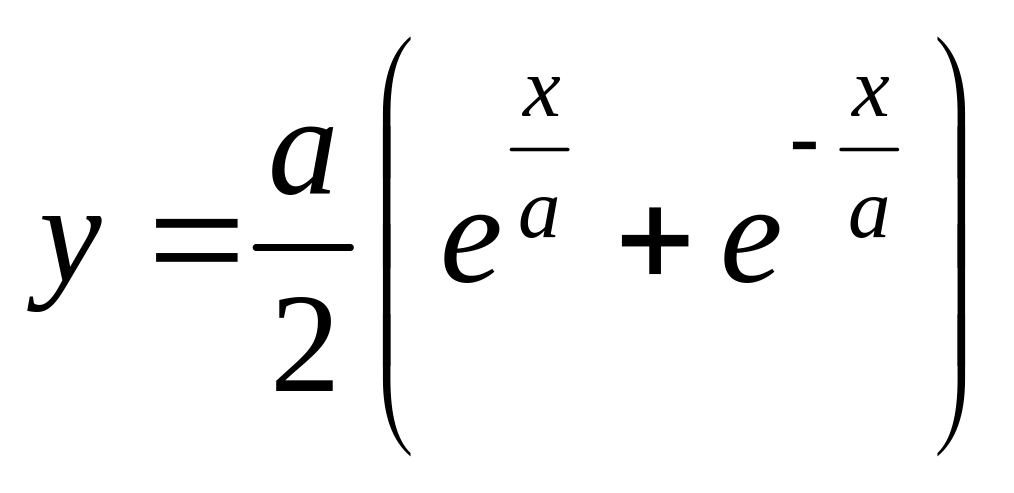 на отрезке
на отрезке
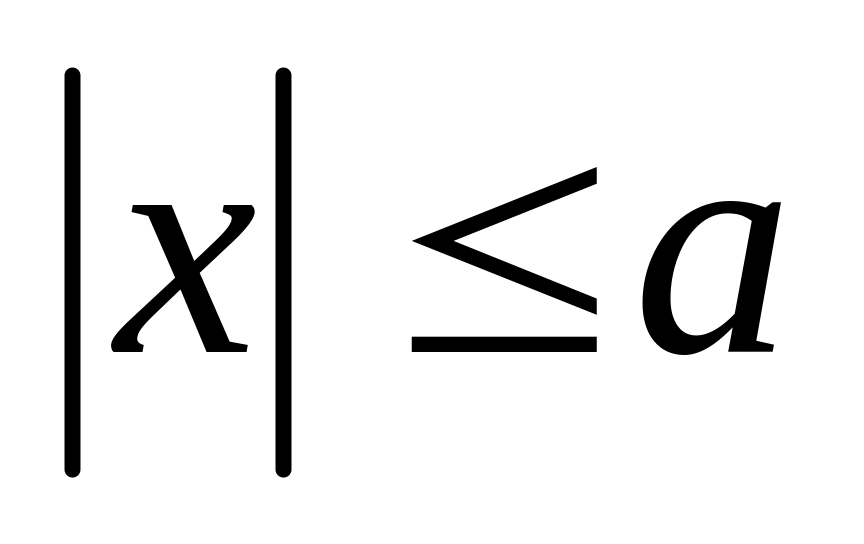 .
.Параболы
 ,
,
 .
.Полукубической параболы
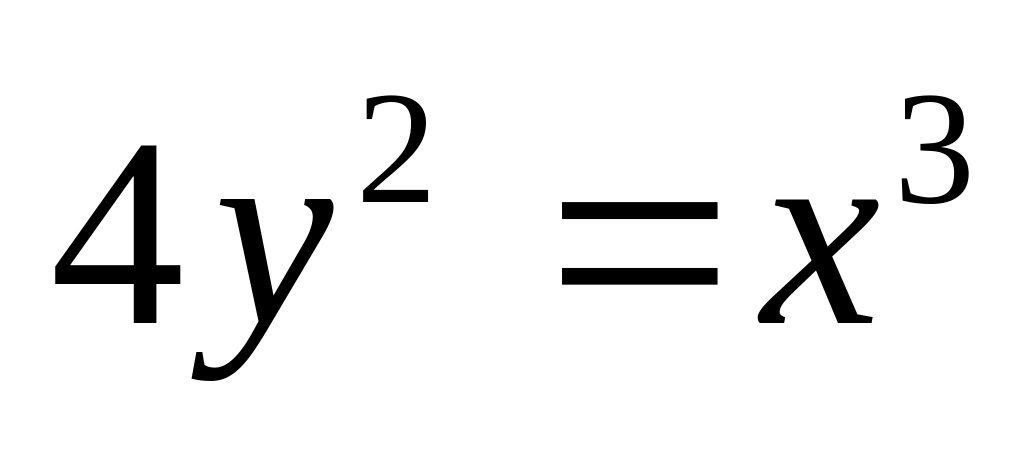 ,
,
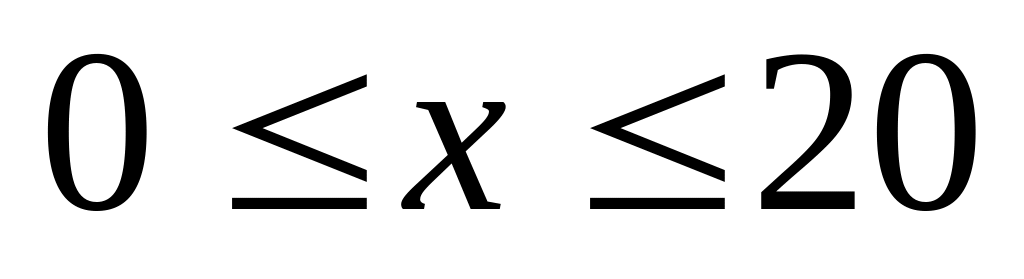 .
.Окружности
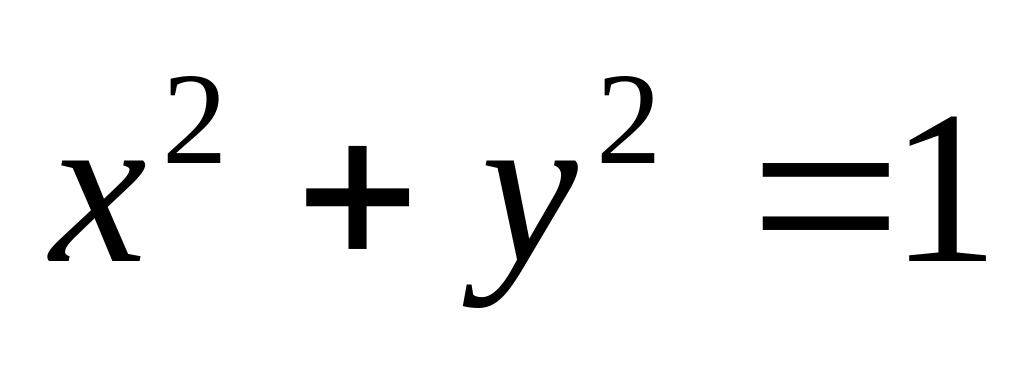 от точки
от точки
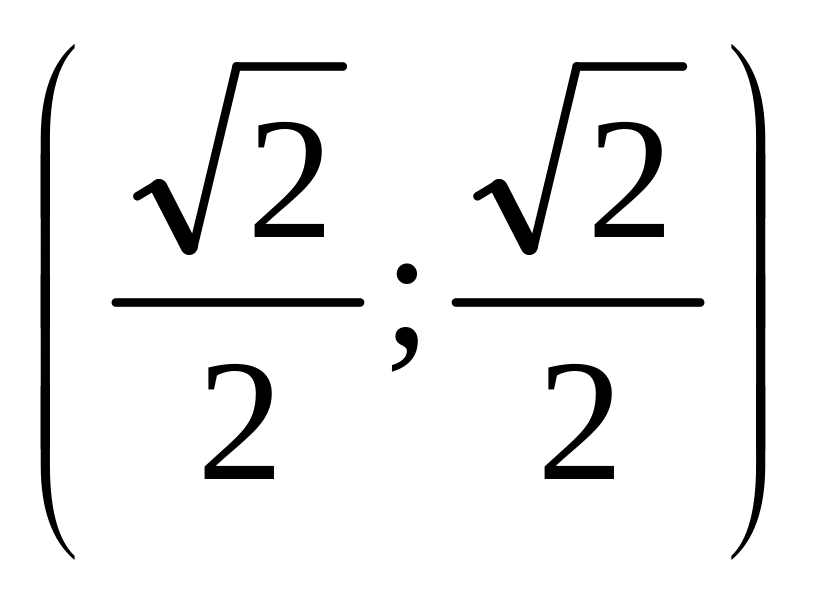 до точки
до точки
 .
.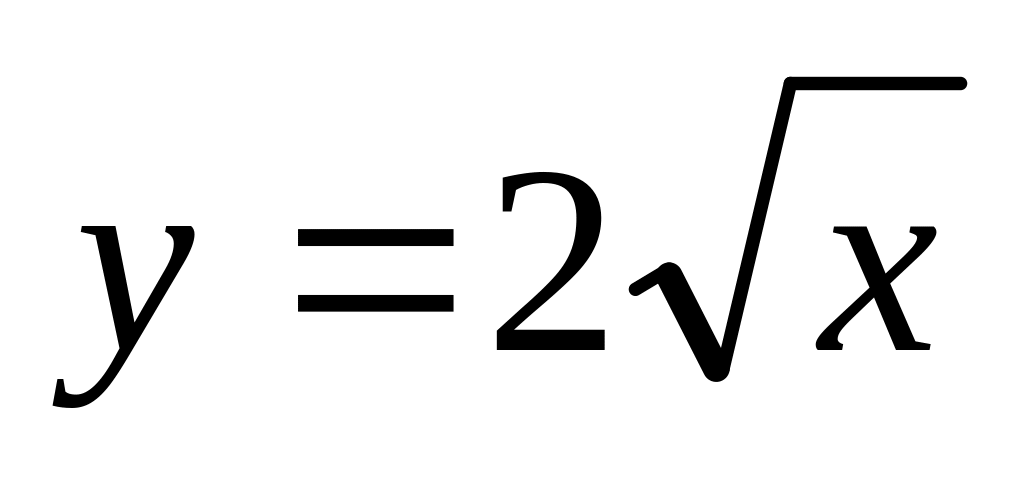 ,
если
,
если
 .
.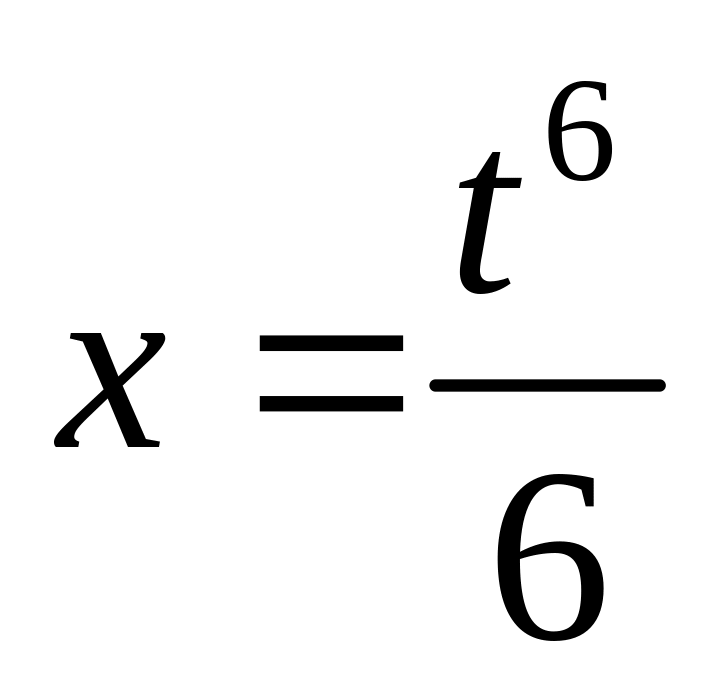 ,
,
 между точками ее пересечения с осями
координат.
между точками ее пересечения с осями
координат.Полукубической параболы
 ,
если
,
если
 .
. ,
если
,
если
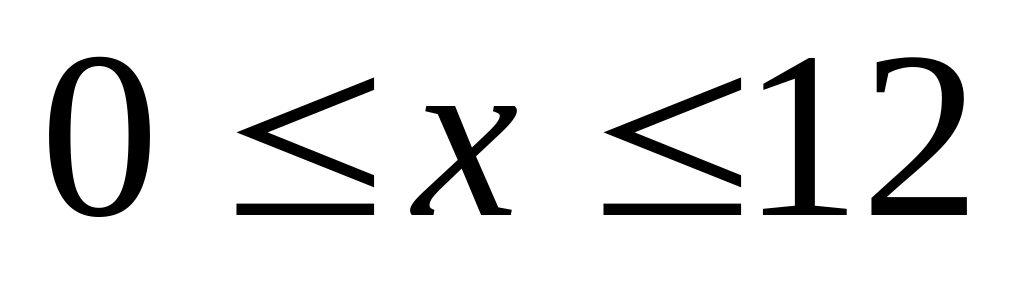 .
.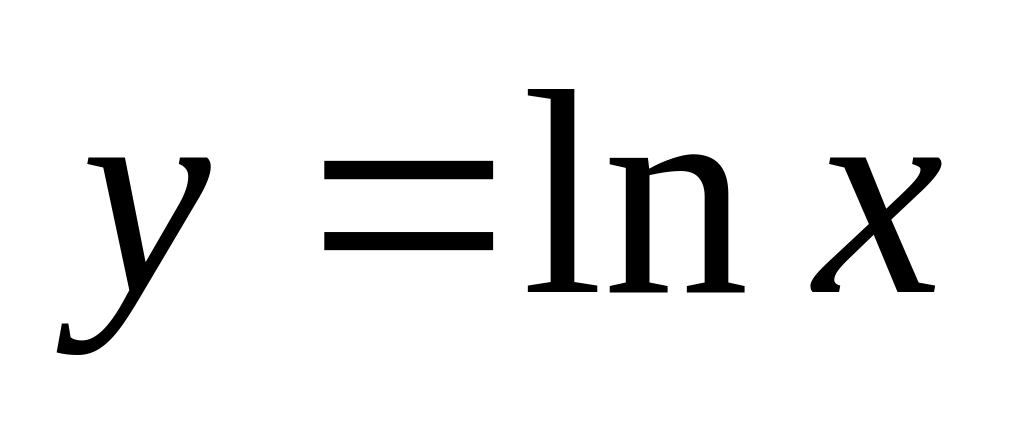 ,
если
,
если
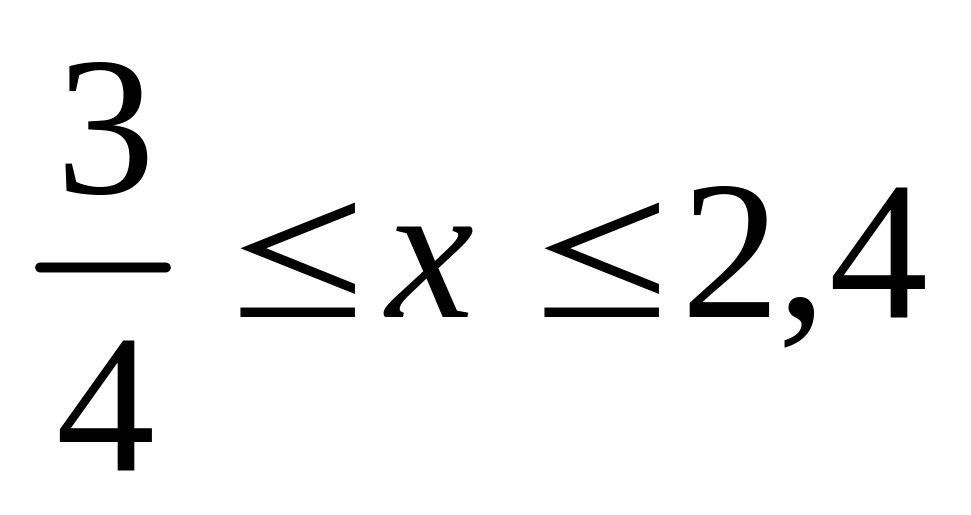 .
.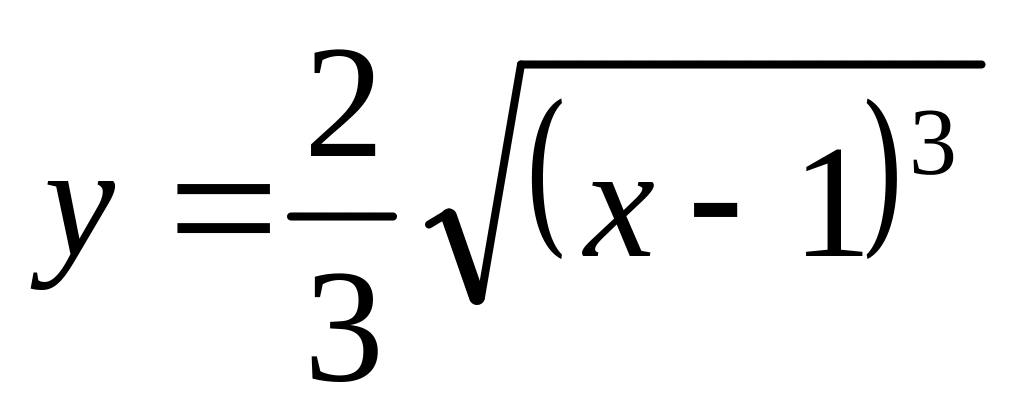 ,
если
,
если
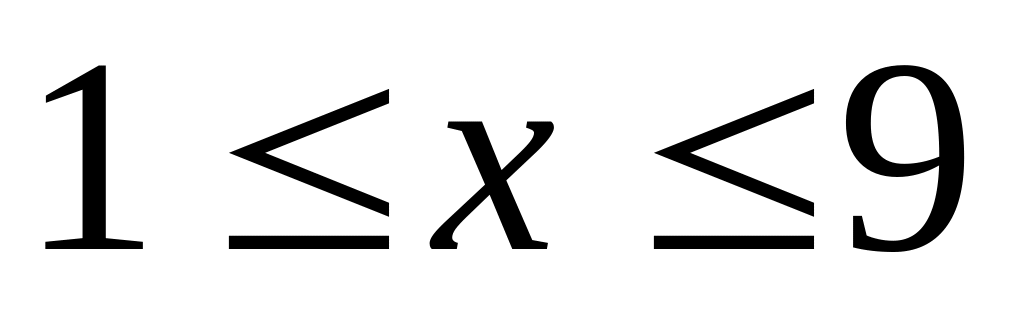 .
.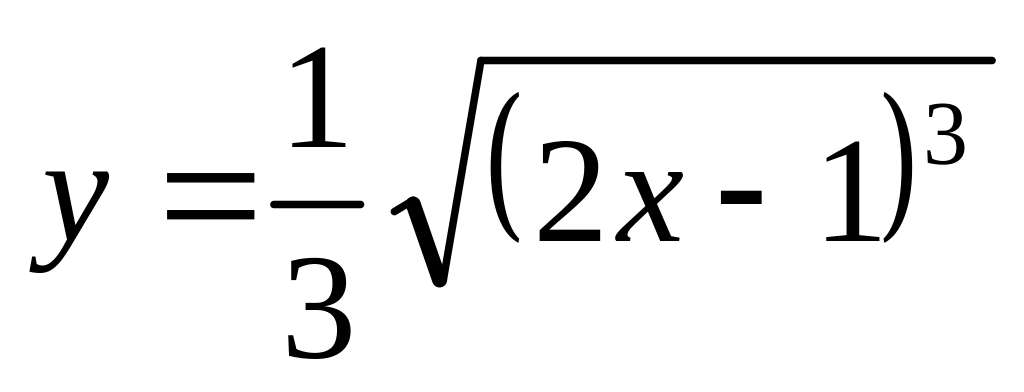 ,
если
,
если
 .
.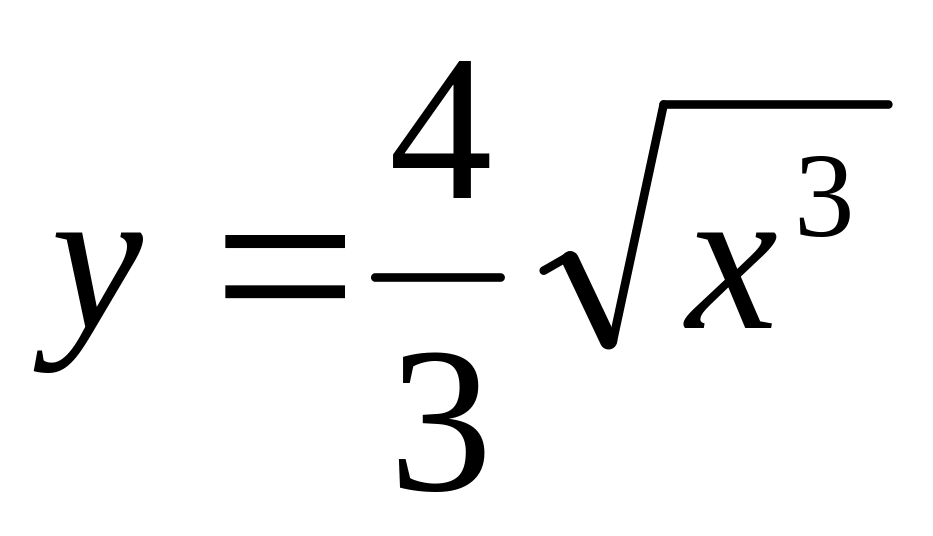 ,
если
,
если
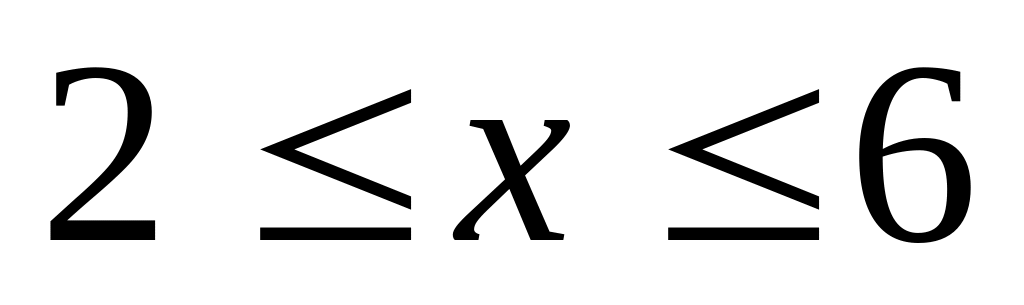 .
. ,
если
,
если
 .
. ,
,
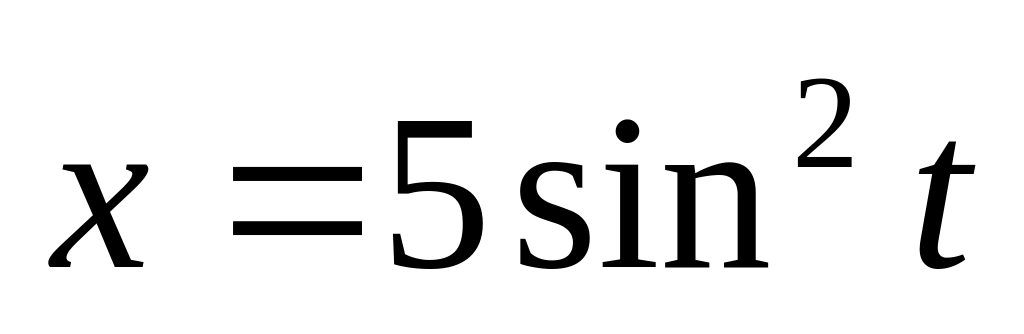 ,
если
,
если
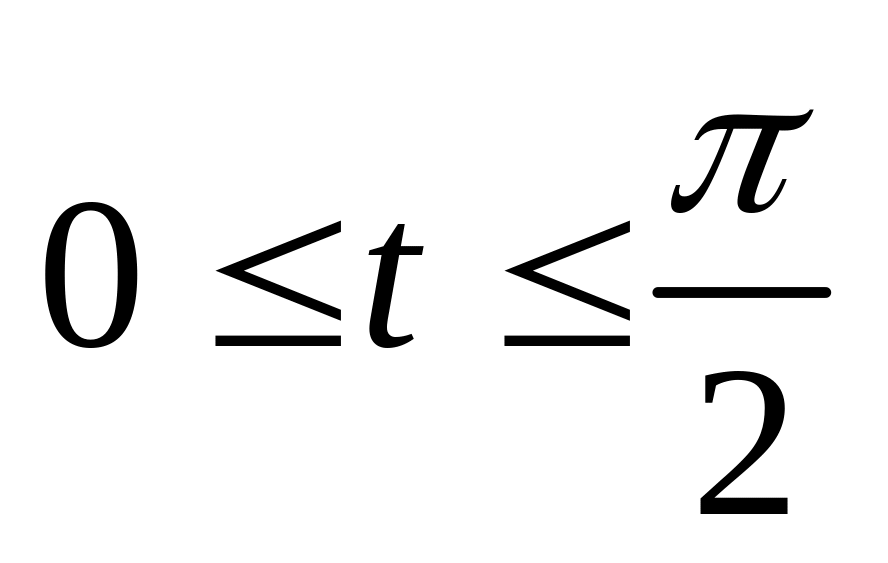 .
.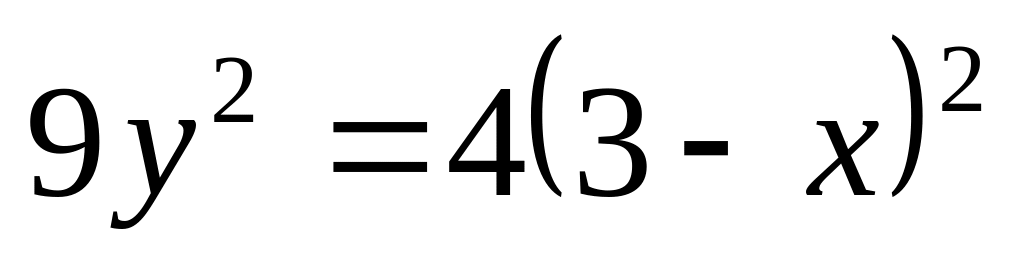 между точками
пересечения с осью
.
между точками
пересечения с осью
.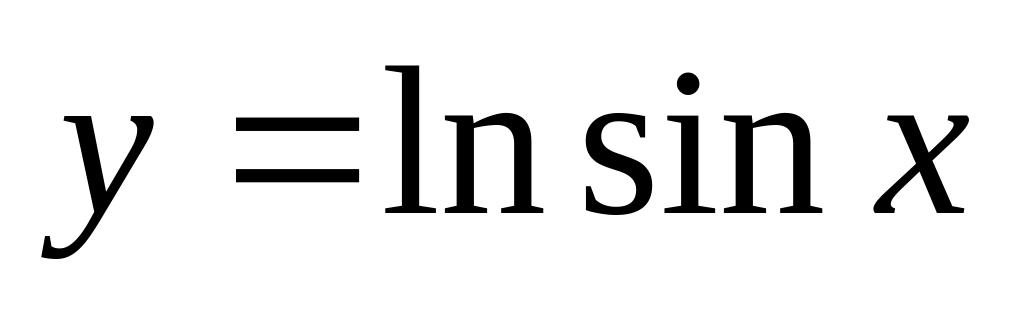 ,
если
,
если
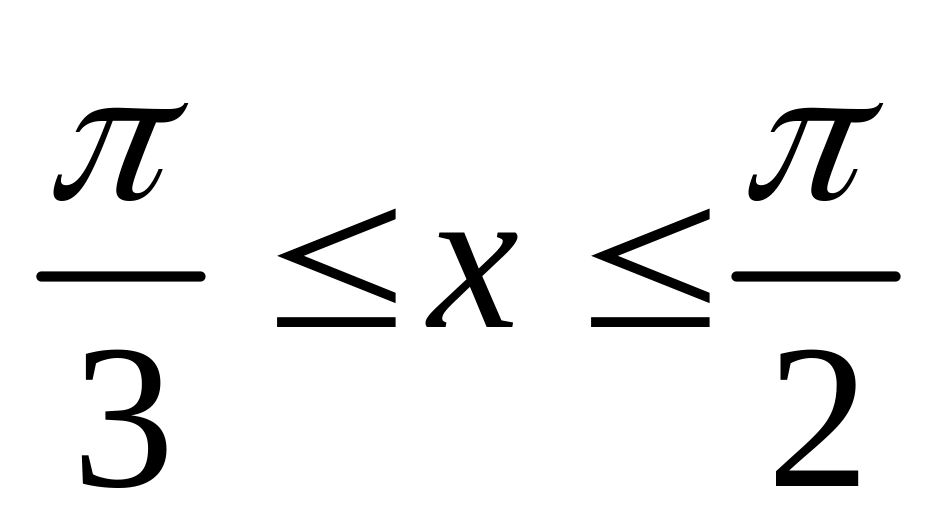 .
. от точки
от точки
 до точки
до точки
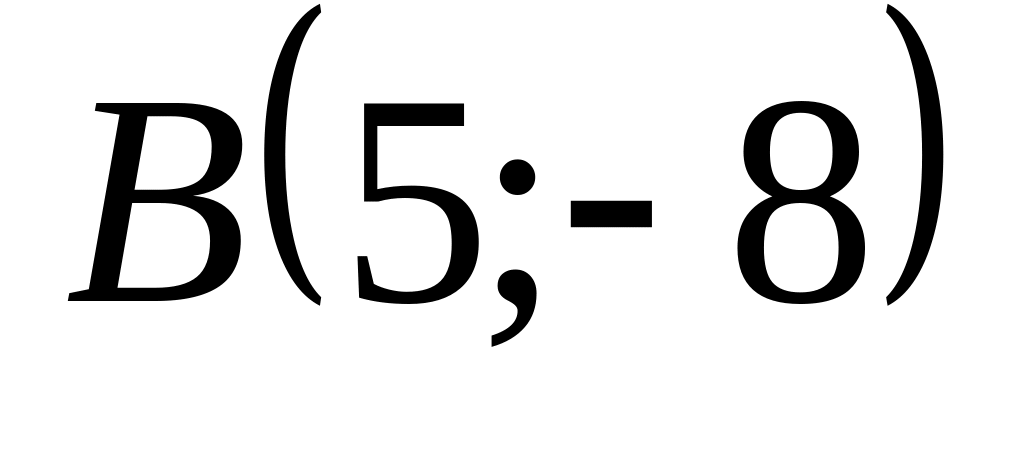 .
.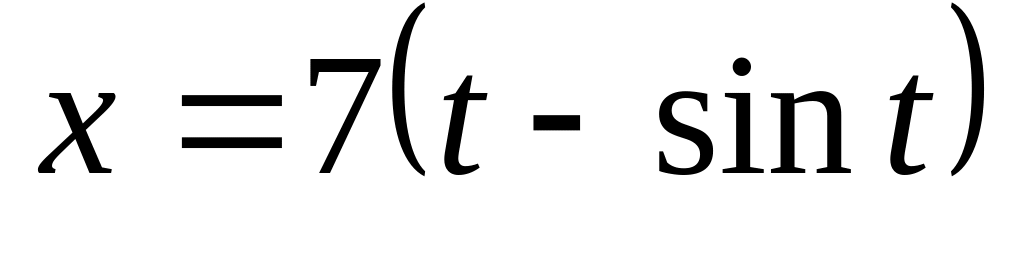 ,
,
 ,
если
,
если
 .
. ,
если
,
если
 .
.
