
- •Введение
- •1. Парная регрессия и корреляция
- •1.1. Решение типовых задач
- •1.2 Контрольные задания
- •2. Множественная регрессия
- •2.1. Решение типовых задач
- •2.1. Контрольные задания
- •3. Системы эконометрических уравнений
- •3.1. Решение типовых задач
- •Система нормальных уравнений составит:
- •3.2. Контрольные задания
- •4. Временные ряды
- •4.1. Решение типовых задач
- •4.2. Контрольные задания
- •5. Контрольные вопросы по курсу
- •Библиографический список
- •Эконометрика
- •400002, Волгоград, пр-т. Университетский, 26
регрессии, нелинейные по оцениваемым параметрам:
степенная
 ;
;показательная
 ;
;экспоненциальная
 .
.
В парной регрессии выбор вида математической функции может быть осуществлен графическим, аналитическим или экспериментальным методом.
Построение уравнения
регрессии сводится к оценке ее параметров.
Для оценки параметров регрессий обычно
используют метод наименьших квадратов
(МНК). МНК позволяет получить такие
оценки параметров, при которых сумма
квадратов отклонений фактических
значений результативного признака y
от теоретических
![]() минимальна, т.е.
минимальна, т.е.
![]() .
.
Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно b0 и b1:
 .
.
Можно воспользоваться готовыми формулами, которые вытекают из этой системы:
![]() .
.
Тесноту связи изучаемых явлений оценивает:
линейный коэффициент парной корреляции rxy для линейной регрессии (
 ):
):
![]() ;
;
индекс корреляции
 для нелинейной регрессии(
для нелинейной регрессии( ):
):
 .
.
Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.
Коэффициент
детерминации характеризует долю
дисперсии, объясняемую регрессией, в
общей дисперсии результативного признака
y:
![]() .
Величина (1–R2)
характеризует
долю дисперсии у,
вызванную влиянием остальных не учтенных
в модели факторов.
.
Величина (1–R2)
характеризует
долю дисперсии у,
вызванную влиянием остальных не учтенных
в модели факторов.
Средняя ошибка аппроксимации – среднее отклонение расчетных значений результативного признака от фактических:
![]() .
.
Допустимый предел
значений
![]() – не более 8-10%.
– не более 8-10%.
Оценивание качества уравнения регрессии по F-критерию Фишера состоит в проверке гипотезы H0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fнабл и критического (табличного) Fкр значений F-критерия Фишера.
 ,
,
где n – число единиц совокупности;
m – число параметров при переменной х.
Fкр – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы (k1=m, k2=n-m–1) и уровне значимости α. Уровень значимости α – вероятность отвергнуть гипотезу при условии что она верна. Обычно принимается равной 0,05 или 0,01.
Если Fкр < Fнабл, то H0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если Fкр > Fнабл, то гипотеза H0 не отклоняется и признается статистическая незначимость и ненадежность уравнения регрессии и показателя тесноты связи.
Для оценки статистической значимости коэффициентов регрессии рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей.
Выдвигается гипотеза H0 о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной стандартной ошибки:
![]() .
.
Стандартные ошибки параметров линейной регрессии определяются по формулам:

где
![]() – оценка остаточной дисперсии.
– оценка остаточной дисперсии.
Сравнивая фактическое и критическое (табличное) значение t-статистики – tкр и tнабл – принимаем или отвергаем гипотезу H0. tкр определяется из таблицы распределения Стьюдента для уровня значимости α и числа степеней свободы df = n-m-1.
Связь между F-критерием Фишера и t-статистикой Стьюдента выражается равенством:
![]() .
.
Если tкр < |tнабл|, то H0 отклоняется, т.е. bj не случайно отличен от нуля и сформировался под влиянием систематически действующего фактора x. Если tкр > |tнабл|, то гипотеза H0 не отклоняется и признается случайная природа формирования bj.
Доверительным интервалом называется такой интервал, относительно которого можно с заранее выбранной вероятностью утверждать, что он содержит значения прогнозируемого показателя.
Интервальная оценка для коэффициентов β0 и β1 определяется по формулам:
![]() .
.
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
Прогнозное значение
yp
определяется путем подстановки в
уравнение регрессии
![]() соответствующего (прогнозного) значения
xp.
Вычисляется средняя стандартная ошибка
прогноза:
соответствующего (прогнозного) значения
xp.
Вычисляется средняя стандартная ошибка
прогноза:
 ;
;
и строится доверительный интервал прогноза:
![]() .
.
1.1. Решение типовых задач
Пример 1. По 10 хозяйствам района известны сведения о дозах внесения удобрений на 1 га зерновых (x) и об урожайности зерновых культур (y):
Таблица 1.1– Исходные данные для построения модели
Урожайность зерновых культур, ц/га |
26,4 |
21,1 |
21,9 |
38,1 |
19,2 |
28,6 |
19,4 |
35,2 |
24,1 |
32,3 |
Доза внесения удобрений на 1 га зерновых, ц д.в. |
3,4 |
3,1 |
3 |
5 |
2,8 |
4,1 |
2,5 |
5,3 |
2,9 |
4 |
Требуется:
1. Для характеристики зависимости y от x рассчитать параметры следующих функций:
а) линейной;
б) степенной;
2. Оценить тесноту связи изучаемых признаков.
3. Оценить каждую модель через среднюю ошибку аппроксимации и F-критерий Фишера.
Решение:
а)
Для расчета
параметров b0
и b1
линейной регрессии
![]() решаем
систему нормальных уравнений относительно
b0
и b1:
решаем
систему нормальных уравнений относительно
b0
и b1:

По исходным данным рассчитываем Σy, Σx, Σxy, Σx2, Σy2.
Таблица 1.2 – Определение параметров модели и оценка её качества
№ |
x |
y |
xy |
x2 |
y2 |
|
|
Ai |
1 |
3,4 |
26,4 |
89,76 |
11,56 |
696,96 |
25,2 |
1,2 |
4,4 |
2 |
3,1 |
21,1 |
65,41 |
9,61 |
445,21 |
23,2 |
-2,1 |
10,1 |
3 |
3 |
21,9 |
65,70 |
9,00 |
479,61 |
22,6 |
-0,7 |
3,1 |
4 |
5 |
38,1 |
190,50 |
25,00 |
1451,61 |
35,9 |
2,2 |
5,8 |
5 |
2,8 |
19,2 |
53,76 |
7,84 |
368,64 |
21,2 |
-2,0 |
10,6 |
6 |
4,1 |
28,6 |
117,26 |
16,81 |
817,96 |
29,9 |
-1,3 |
4,5 |
7 |
2,5 |
19,4 |
48,50 |
6,25 |
376,36 |
19,2 |
0,2 |
0,8 |
8 |
5,3 |
35,2 |
186,56 |
28,09 |
1239,04 |
37,9 |
-2,7 |
7,6 |
9 |
2,9 |
24,1 |
69,89 |
8,41 |
580,81 |
21,9 |
2,2 |
9,1 |
10 |
4 |
32,3 |
129,20 |
16,00 |
1043,29 |
29,2 |
3,1 |
9,5 |
Итого |
36,1 |
266,3 |
1016,54 |
138,57 |
7499,49 |
266,3 |
0,0 |
65,6 |
Ср. знач. |
3,61 |
26,63 |
101,65 |
13,86 |
749,95 |
- |
- |
6,6 |
![]() .
.
Решив систему уравнений, получим следующие значения параметров:
b1 = 6,66, b0 = 2,59.
Параметры регрессии рассчитаем с помощью формул:
![]() ,
,
![]() .
.
Уравнение
регрессии имеет вид:
![]() .
.
С увеличением дозы внесения удобрений на 1 га зерновых на 1 ц д.в. урожайность зерновых культур увеличивается на 6,66 ц/га.
Рассчитаем линейный коэффициент парной корреляции:
![]() .
.
Связь между рассматриваемыми признаками сильная, прямая.
Определим коэффициент детерминации:
![]()
Вариация результата на 90% объясняется вариацией фактора x. На долю прочих факторов, не учитываемых в регрессии, приходится 10%.
Подставляя
в уравнение регрессии фактические
значения x,
определим
теоретические
(расчетные) значения
![]() .
Найдем величину средней ошибки
аппроксимации:
.
Найдем величину средней ошибки
аппроксимации:
![]() .
.
Ошибка аппроксимации показывает хорошее соответствие расчетных и фактических данных: среднее отклонение составляет 6,6 %.
Рассчитаем F-критерий:
![]() .
.
Fкр.
находим по таблице значений F-критерия
Фишера при уровне значимости![]() и степенях свободы k1=1,
k2=8:
Fкр=5,32.
и степенях свободы k1=1,
k2=8:
Fкр=5,32.
Т.к. Fкр< Fнабл (5,32 < 72), отклоняется гипотеза Н0 о случайной природе выявленной зависимости и статистической незначимости параметров уравнения и показателя тесноты связи.
б)
Построению
нелинейной модели
предшествует
процедура линеаризации переменных.
Линеаризация степенной модели![]() производится путем логарифмирования
обеих частей уравнения:
производится путем логарифмирования
обеих частей уравнения:
![]()
![]()
где Y=lg y, X=lg x, В0=lg b0.
Для расчетов используем данные таблицы 1.3.
Таблица 1.3 – Определение параметров модели и оценка её качества
№ |
X |
Y |
XY |
X2 |
Y2 |
|
|
|
Ai |
|
1 |
0,5315 |
1,4216 |
0,7556 |
0,2825 |
2,0210 |
25,2 |
1,2 |
1,5 |
4,6 |
0,1 |
2 |
0,4914 |
1,3243 |
0,6507 |
0,2414 |
1,7537 |
23,1 |
-2,0 |
4,1 |
9,6 |
30,6 |
3 |
0,4771 |
1,3404 |
0,6396 |
0,2276 |
1,7968 |
22,4 |
-0,5 |
0,3 |
2,4 |
22,4 |
4 |
0,6990 |
1,5809 |
1,1050 |
0,4886 |
2,4993 |
36,0 |
2,1 |
4,4 |
5,5 |
131,6 |
5 |
0,4472 |
1,2833 |
0,5738 |
0,2000 |
1,6469 |
21,0 |
-1,8 |
3,4 |
9,5 |
55,2 |
6 |
0,6128 |
1,4564 |
0,8924 |
0,3755 |
2,1210 |
30,0 |
-1,4 |
1,8 |
4,8 |
3,9 |
7 |
0,3979 |
1,2878 |
0,5125 |
0,1584 |
1,6584 |
18,9 |
0,5 |
0,2 |
2,4 |
52,3 |
8 |
0,7243 |
1,5465 |
1,1201 |
0,5246 |
2,3918 |
38,0 |
-2,8 |
7,9 |
8,0 |
73,4 |
9 |
0,4624 |
1,3820 |
0,6390 |
0,2138 |
1,9100 |
21,7 |
2,4 |
5,6 |
9,8 |
6,4 |
10 |
0,6021 |
1,5092 |
0,9086 |
0,3625 |
2,2777 |
29,3 |
3,0 |
9,1 |
9,3 |
32,1 |
Итого |
5,4455 |
14,1325 |
7,7974 |
3,0748 |
20,0766 |
265,7 |
0,6 |
38,2 |
65,9 |
407,9 |
Ср. знач. |
0,5446 |
1,4132 |
0,7797 |
0,3075 |
2,0077 |
- |
- |
- |
6,6 |
- |
Рассчитаем значения параметров В0 и b1:
![]() ,
,
![]() .
.
Получим
линейное уравнение:
![]() .
.
Выполнив
его потенцирование, получим:
![]() .
.
Подставляя
в данное уравнение фактические значения
x,
получаем
теоретические значения результата
.
По ним рассчитаем индекс корреляции
![]() и среднюю ошибку аппроксимации
и среднюю ошибку аппроксимации
![]() :
:
 ,
,
![]() .
.

Так как Fкр < Fнабл (5,32 < 76,6), отвергается гипотеза Н0 о статистической незначимости параметров степенного уравнения.
Пример 2. По 10 территориям региона приводятся данные за 200Х год (таблица 1.4).
Таблица 1.4 – Исходные данные для построения модели
Себестоимость единицы продукции у, д.е., |
12,0 |
12,5 |
12,2 |
13,3 |
12,0 |
13,4 |
13,5 |
13,2 |
14,4 |
15,2 |
Объем производства х, ед. |
310 |
322 |
325 |
330 |
340 |
382 |
384 |
328 |
380 |
386 |
Требуется:
1. Построить линейное уравнение парной регрессии y от x.
2. Рассчитать линейный коэффициент парной корреляции.
3. Оценить статистическую значимость параметров регрессии с помощью t-критерия Стьюдента.
4. Дать точечный и интервальный прогноз себестоимости единицы продукции с вероятностью 0,95, принимая уровень объема производства равным 370 ед.
Решение:
1. Для расчета параметров уравнения линейной регрессии строим расчетную таблицу (таблица 1.5).
Таблица 1.5 Определение параметров модели и оценка её качества
№ |
x |
y |
yx |
x2 |
y2 |
|
|
1 |
310 |
12,0 |
3720,0 |
96100 |
144,00 |
12,12 |
-0,12 |
2 |
322 |
12,5 |
4025,0 |
103684 |
156,25 |
12,45 |
0,05 |
3 |
325 |
12,2 |
3965,0 |
105625 |
148,84 |
12,53 |
-0,33 |
4 |
330 |
13,3 |
4389,0 |
108900 |
176,89 |
12,66 |
0,64 |
5 |
340 |
12,0 |
4080,0 |
115600 |
144,00 |
12,93 |
-0,93 |
6 |
382 |
13,4 |
5118,8 |
145924 |
179,56 |
14,07 |
-0,67 |
7 |
384 |
13,5 |
5184,0 |
147456 |
182,25 |
14,13 |
-0,63 |
8 |
328 |
13,2 |
4329,6 |
107584 |
174,24 |
12,61 |
0,59 |
9 |
380 |
14,4 |
5472,0 |
144400 |
207,36 |
14,02 |
0,38 |
10 |
386 |
15,2 |
5867,2 |
148996 |
231,04 |
14,18 |
1,02 |
Итого |
3487 |
131,7 |
46150,6 |
1224269 |
1744,43 |
131,7 |
- |
Ср.знач. |
348,7 |
13,17 |
4615,06 |
122426,9 |
174,443 |
- |
- |
![]() ;
;
![]() .
.
Получено уравнение
регрессии:
![]() .
.
С увеличением объема производства на единицу, себестоимость единицы продукции возрастает в среднем на 0,0272 д.е.
2. Тесноту линейной связи оценивает коэффициент корреляции:
![]() ;
;
![]() .
.
Это означает, что 62% вариации себестоимости единицы продукции (y) объясняется вариацией фактора x – объема производства.
3. Оценку статистической значимости параметров регрессии проведем с помощью t-статистики Стьюдента и путем расчета доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля: b0=b1=0.
tкр для числа степеней свободы df=10-2=8 и α=0,05 составит 2,31.
Определим стандартные
ошибки
![]() :
:
![]() ;
;
![]()
Тогда
![]()
Фактическое
значение t-статистики
для коэффициента b1
превосходит табличное значение
![]() ,
поэтому
гипотеза Н0
отклоняется, т.е.
b1
не случайно
отличен от нуля, а статистически значим.
,
поэтому
гипотеза Н0
отклоняется, т.е.
b1
не случайно
отличен от нуля, а статистически значим.
Критическое
значение t-статистики
превосходит фактическое значение для
коэффициента b0
![]() ,
поэтому
гипотеза Н0
принимается, т.е.
b0
случайно
отличен от нуля и статистически незначим.
,
поэтому
гипотеза Н0
принимается, т.е.
b0
случайно
отличен от нуля и статистически незначим.
Рассчитаем доверительный интервал для b0 и b1:
![]()
![]() .
.
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью p=1-α=0,95 параметр b1, находясь в указанных границах, не принимает нулевых значений, т.е. является статистически значимым и существенно отличен от нуля. Параметр b0 является статистически незначимым.
4.
Полученные оценки уравнения регрессии
позволяют использовать его для прогноза.
Точечный прогноз себестоимости при
прогнозном значении объема производства
хр=370
ед. составит:
![]() д.е.
д.е.
Чтобы получить интервальный прогноз, найдем стандартную ошибку прогноза:
![]()
Доверительный интервал прогнозируемой себестоимости составит:
![]() ,
,
т.е. при объеме производства, равном 370 ед., себестоимость единицы продукции с надежностью 0,95 находится в пределах от 12,04 д.е. до 15,46 д.е.
1.2 Контрольные задания
Задание к задачам 1-10. Имеются данные о расходах населения на продукты питания (y) и доходах семьи (x), ден. ед. для 8 районов.
1. Для характеристики зависимости y от x рассчитайте параметры следующих функций:
а) линейной;
б) степенной;
2.Оцените тесноту связи изучаемых признаков.
3.Оцените каждую модель через среднюю ошибку аппроксимации и F-критерий Фишера.
Таблица 1.6 – Исходные данные для моделирования (варианты 1-10)
Задача |
Признак |
Значения признака |
|||||||
1 |
y |
90 |
120 |
180 |
220 |
260 |
290 |
330 |
380 |
x |
120 |
310 |
530 |
740 |
960 |
1180 |
1450 |
1870 |
|
2 |
y |
95 |
125 |
185 |
225 |
260 |
270 |
325 |
350 |
x |
125 |
300 |
510 |
720 |
950 |
1150 |
1450 |
1861 |
|
3 |
y |
90 |
120 |
180 |
220 |
260 |
290 |
330 |
380 |
x |
110 |
300 |
515 |
730 |
940 |
1100 |
1450 |
1850 |
|
4 |
y |
85 |
110 |
155 |
210 |
245 |
285 |
325 |
360 |
x |
120 |
310 |
530 |
740 |
960 |
1180 |
1450 |
1870 |
|
5 |
y |
80 |
100 |
130 |
165 |
200 |
255 |
300 |
345 |
x |
150 |
280 |
330 |
500 |
880 |
1050 |
1350 |
1800 |
|
6 |
y |
100 |
150 |
220 |
300 |
330 |
350 |
380 |
400 |
x |
200 |
280 |
350 |
600 |
750 |
1200 |
1400 |
1900 |
|
7 |
y |
85 |
110 |
155 |
210 |
245 |
285 |
325 |
360 |
x |
150 |
280 |
330 |
500 |
880 |
1050 |
1350 |
1800 |
|
8 |
y |
87 |
95 |
115 |
135 |
150 |
200 |
250 |
335 |
x |
180 |
200 |
250 |
310 |
650 |
980 |
1450 |
1750 |
|
9 |
y |
90 |
120 |
180 |
220 |
260 |
290 |
330 |
380 |
x |
200 |
280 |
350 |
600 |
750 |
1200 |
1400 |
1900 |
|
10 |
y |
87 |
95 |
115 |
135 |
150 |
200 |
250 |
335 |
x |
120 |
310 |
530 |
740 |
960 |
1180 |
1450 |
1870 |
|
Задание к задачам 11-20.
1. Определите параметры уравнения парной линейной регрессии и дайте интерпретацию коэффициента регрессии.
2. Оцените тесноту связи с помощью коэффициентов корреляции и детерминации, проанализируйте их значения.
3. С вероятностью 0,95 оцените статистическую значимость параметров уравнения регрессии по критерию Стьюдента.
4. Рассчитайте
прогнозное значение результата y,
если прогнозное значение фактора х
составит 1,062 от среднего уровня (![]() ).
Определите доверительный интервал
прогноза (для
= 0,05).
).
Определите доверительный интервал
прогноза (для
= 0,05).
Таблица 1.7– Исходные данные для моделирования (варианты 11-20)
Задача |
Условие |
Функция |
11 |
Оцените зависимость среднедушевых денежных расходов за месяц, тыс. руб., (y1) от среднемесячной начисленной заработной платы работающих в экономике, тыс. руб., x1 |
|
12 |
Выявить и оценить зависимость сальдированного финансового результата (прибыли) за год, млрд руб., (y2) от инвестиций в основной капитал в 2006 г., млрд руб., x2 |
|
13 |
Выявить и оценить зависимость между сальдированным финансовым результатом (прибылью) за год, млрд руб., y2 и инвестициями в основной капитал в предыдущем 2005 г., млрд. руб., x3. |
|
14 |
Выявить и оценить зависимость между стоимостью валового регионального продукта (вновь созданная стоимость) за год, млрд руб., y4 и инвестициями в основной капитал в 2006 г., млрд руб., x2 |
|
15 |
Выявить и оценить зависимость расходов консолидированных бюджетов субъектов РФ, млрд руб., y5 от доходов консолидированных бюджетов субъектов РФ, млрд руб., x5 |
|
16 |
Выявить и оценить зависимость доходов консолидированных бюджетов субъектов РФ, млрд руб., y6 от стоимости валового регионального продукта (вновь созданной стоимости) за 2005 г., млрд руб., x6 |
|
17 |
Выявить и оценить зависимость оборота розничной торговли за год, млрд руб., y7 от среднегодовой численности экономически активного населения, млн чел., x7 |
|
18 |
Выявить и оценить зависимость между среднедушевыми денежными расходами за месяц, тыс. руб., y8 и среднемесячной начисленной заработной платой работающих в экономике, тыс. руб., x8 |
|
19 |
Выявить и оценить зависимость сальдированного финансового результата (прибыли) за 2006 г., млн руб., y9 от инвестиций в основной капитал в 2006 г., млрд руб., x9. |
|
20 |
Выявить и оценить зависимость между расходованием средств пенсионного фонда за 2005 г. по субъектам РФ, млрд руб., (y10) и поступлением средств в пенсионный фонд по субъектам РФ, млрд руб., x10 |
|
Таблица 1.8 - Исходные данные к задачам 11-17
-
Территории Северо-Западного федерального округа
Среднедушевые денежные расходы за месяц, тыс. руб.
Среднемесячная заработная плата
работающих в экономике, тыс. руб.
Прибыль за год, млрд руб.
Инвестиции в основной капитал в 2006 г., млрд. руб.
Инвестиции в основной капитал в предыдущем 2005 г., млрд руб.
Валовой региональный продукт за год,
млрд руб.
Расходы консолидированных бюджетов субъектов РФ, млрд руб.
Доходы консолидированных бюджетов
субъектов РФ, млрд руб.
Валовой региональный продукт,
млрд руб.
Оборот розничной торговли за год,
млрд руб.
Среднегодовая численность экономически активного населения, млн чел.
y1
x1
y2
x2
x3
y4
y5
x5 (y6)
x6
y7
x7
Республика Карелия
4,99
7,00
2,21
12,60
9,63
48,1
9,86
8,49
48,1
19,9
0,399
Республика
Коми
7,84
9,58
17,45
30,20
25,92
113,5
17,28
16,34
113,5
44,5
0,607
Архан-гельская обл.
5,26
7,85
8,60
30,50
31,60
107,6
18,78
18,28
107,6
35,7
0,763
Вологодская обл.
4,91
6,94
61,05
41,45
17,71
114,2
16,75
16,85
114,2
26,8
0,655
Калининградская обл.
4,69
6,21
5,76
18,11
14,87
51,3
9,71
9,32
51,3
22,7
0,502
Ленин-градская обл.
3,72
6,78
33,38
67,02
44,03
132,4
18,97
18,1
132,4
30,6
0,873
Мурманская обл.
7,10
10,40
16,22
13,53
13,70
81,6
13,68
12,42
81,6
161,9
2,483
Новгородская обл.
4,09
5,56
3,88
7,95
9,13
39,1
6,36
5,95
39,1
34,2
0,572
Псковская обл.
4,01
4,67
0,75
5,75
3,86
30,3
7,51
7,05
30,3
15,6
0,371
Таблица 1.9 - Исходные данные к задачам 18-20
-
Территории Приволжского федерального округа
Среднедушевые денежные расходы за месяц в 2006 г., тыс.руб.
Среднемесячная начисленная заработная плата работающих в экономике в 2006 г., тыс. руб.
Прибыль за 2006 г., млн руб.
Инвестиции в основной капитал в 2006 г.,
млрд. руб.
Расходование средств пенсионного фонда за 2005 г. по субъектам РФ, млрд. руб.
Поступление средств в пенсионный фонд по субъектам РФ за 2005 г., млрд. руб.
Валовой региональный продукт за
2005 г., млрд. руб.
y8
x8
y9
x9
y10
x10
y11
Республика
Башкортостан
4,62
5,5
43,4
62,4
19,7
17,3
279,7
Республика Марий Эл
2,48
3,9
0,6
5,8
3,5
2,6
24,6
Республика Мордовия
2,65
4,09
1,6
10,4
4,9
3,6
36,9
Республика Татарстан
4,78
5,55
70,0
86,6
18,9
17,8
319,1
Республика Удмуртия
3,4
5,16
6,4
15,4
7,9
7,3
97,7
Чувашская республика
3,12
4,06
3,0
14,2
6,4
5,1
50,2
Кировская обл.
3,69
4,55
3,2
9,5
8,7
6,6
62,4
Нижегородская обл.
4,71
5,17
24,2
48,5
21,8
17,5
222,4
Оренбургская обл.
3,34
4,87
19,8
27,7
11,1
8,8
125,2
Пензенская обл.
3,54
4,22
1,8
10,7
8,5
5,7
49,2
Пермская обл.
5,82
6,42
43,5
48,2
15,3
14,1
232,1
Самарская обл.
7,01
6,31
2,8
55,0
18,2
17,0
274,9
Саратовская обл.
3,51
4,49
8,3
23,8
13,9
10,3
131,3
Ульяновская обл.
3,43
4,47
1,4
11,3
7,6
5,7
58,3
2. Множественная регрессия
Множественная регрессия – уравнение связи с несколькими переменными:
![]()
где y – зависимая переменная (результативный признак);
x1, x2, …, xp – независимые переменные (факторы).
Для построения уравнения множественной регрессии чаще используются следующие функции:
линейная –
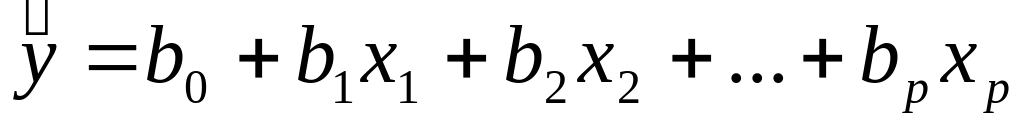 ;
;степенная –
 ;
;экспонента –
 ;
;парабола второго порядка –
![]() .
.
Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов (МНК). Для линейных уравнений и нелинейных уравнений, приводимых к линейным, строится следующая система нормальных уравнений:
![]()
Для ее решения может быть применен метод определителей.
![]() ,
,
где ∆ – определитель системы;
∆b0, ∆b1, …, ∆bp – частные определители, которые получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.
Другой вид уравнения множественной регрессии – уравнение регрессии в стандартизированном масштабе:
![]() ,
,
где βi – стандартизированные коэффициенты регрессии;
![]() –
стандартизированные
переменные.
–
стандартизированные
переменные.
К уравнению множественной регрессии в стандартизированном масштабе применим МНК. Стандартизированные коэффициенты регрессии определяются из следующей системы уравнений:
![]()
![]()
Связь коэффициентов множественной регрессии bi со стандартизированными коэффициентами βi описывается соотношением:
![]() .
.
Параметр b0
определяется
как
![]() .
.
Средние значения
коэффициентов эластичности рассчитываются
по формуле:
![]() .
.
Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции:
 .
.
Значение индекса
множественной корреляции лежит в
пределах от 0 до 1 и должно быть больше
или равно максимальному парному индексу
корреляции:
![]() .
Индекс множественной корреляции для
уравнения в стандартизированном масштабе
можно записать в виде:
.
Индекс множественной корреляции для
уравнения в стандартизированном масштабе
можно записать в виде:
![]() .
.
Коэффициент (индекс) множественной детерминации рассчитывается как квадрат индекса множественной корреляции.
Для того, чтобы не допускать возможного завышения тесноты связи при небольших объемах выборок, применяется скорректированный индекс детерминации:
![]() .
.
Чем больше m
(число параметров при переменных х),
тем сильнее различия
![]() и
и
![]() .
.
Одним из условий
построения уравнения множественной
регрессии является независимость
действия факторов. Считается, что две
переменные явно коллинеарны, т.е.
находятся между собой в линейной
зависимости, если парный коэффициент
корреляции
![]() .
Если факторы коллинеарны, то они дублируют
друг друга и один из них рекомендуется
исключить из регрессии.
.
Если факторы коллинеарны, то они дублируют
друг друга и один из них рекомендуется
исключить из регрессии.
При наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, для ее оценки может использоваться определитель матрицы парных коэффициентов корреляции. Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ниже надежность результатов множественной регрессии.
Частные коэффициенты (или индексы) корреляции, измеряющие влияние на y фактора xi при неизменном уровне других факторов можно определить по рекуррентной формуле:
 .
.
Частные коэффициенты корреляции изменяются в пределах от -1 до 1.
Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается.
Значимость уравнения множественной регрессии в целом оценивается с помощью F-критерия Фишера:
 ,
,
где m – число параметров при переменных x;
p – количество независимых переменных.
Непосредственному
расчету F-критерия
предшествует анализ дисперсии. Центральное
место в нем занимает разложение общей
суммы квадратов
отклонений переменной y
от среднего значения
![]() на две части – «объясненную» и
«остаточную»:
на две части – «объясненную» и
«остаточную»:
![]()
Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим дисперсию на одну степень свободы D.
![]()
Сопоставляя объясненную (факторную) и остаточную дисперсии в расчете на одну степень свободы, получим величину F-критерия для проверки гипотезы Н0: Dфакт=Dост (F=Dфакт/Dост).
Частный F-критерий оценивает статистическую значимость присутствия каждого из факторов в уравнении. В общем виде для фактора xi частный F-критерий определяется по формуле:
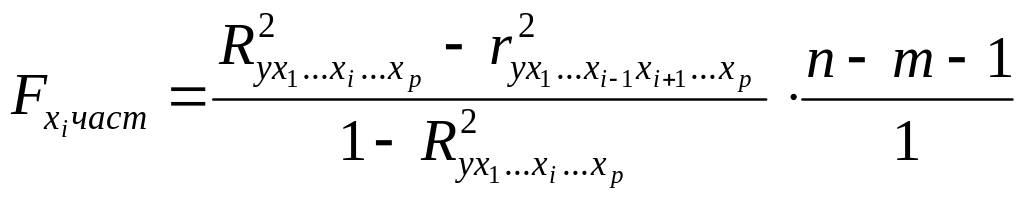 .
.
Оценка значимости коэффициентов регрессии с помощью t-критерия Стьюдента сводится к вычислению значения
![]() ,
,
где Sbi – стандартная ошибка коэффициента регрессии bi, она определяется по следующей формуле:
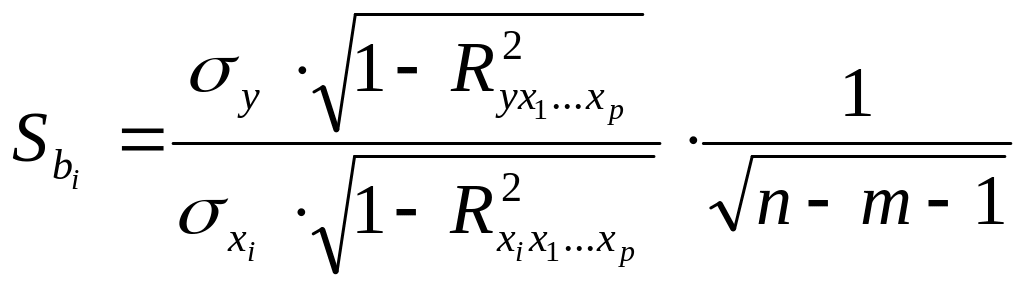 .
.
При оценке параметров уравнения регрессии по МНК делаются определенные предпосылки (теорема Гаусса-Маркова) относительно случайной составляющей ε:
случайный характер остатков;
нулевая средняя величина остатков, не зависящая от хi;
гомоскедастичность – дисперсия каждого отклонения εi одинакова для всех значений х;
отсутствие автокорреляции остатков. Значения остатков εi распределены независимо друг от друга;
остатки подчиняются нормальному распределению.
Если распределение остатков εi не соответствует некоторым предпосылкам МНК, то следует корректировать модель.
2.1. Решение типовых задач
Пример 1. Торговое предприятие имеет сеть, состоящую из 12 магазинов, информация о деятельности которых представлена в таблице 2.1.
Требуется:
1. Построить линейное уравнение множественной регрессии и пояснить экономический смысл его параметров.
2. Определить стандартизованные коэффициенты регрессии.
3. Рассчитать частные коэффициенты эластичности, сравнить их с β1 и β2, пояснить различия между ними.
4. Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции.
5. Провести дисперсионный анализ для проверки статистической значимости уравнения множественной регрессии и его показателя тесноты связи на уровне значимости α=0,05.
6. С помощью частных F-критериев Фишера оценить, насколько целесообразно включение в уравнение множественной регрессии фактора х1 после фактора х2 и насколько целесообразно включение х2 после х1.
7. Оценить с помощью t-критерия Стьюдента статистическую значимость коэффициентов при переменных х1 и х2 множественного уравнения регрессии.
Таблица 2.1 – Исходные данные для моделирования
Номер магазина |
Годовой товарооборот, млн. руб. |
Торговая площадь, тыс. м2 |
Среднее число посетителей, тыс. чел. |
y |
x1 |
x2 |
|
1 |
19,76 |
0,24 |
8,25 |
2 |
38,09 |
0,31 |
10,24 |
3 |
40,95 |
0,55 |
9,31 |
4 |
41,08 |
0,48 |
11,01 |
5 |
56,29 |
0,78 |
8,54 |
6 |
68,51 |
0,98 |
7,51 |
7 |
75,01 |
0,94 |
12,36 |
8 |
89,05 |
1,21 |
10,81 |
9 |
91,13 |
1,29 |
9,89 |
10 |
91,26 |
1,12 |
13,72 |
11 |
99,84 |
1,29 |
12,27 |
12 |
108,55 |
1,49 |
13,92 |
Решение:
1. Линейное уравнение множественной регрессии y от x1 и x2 имеет вид:
=b0+b1x1+b2x2.
Расчет его параметров произведем в MS Excel с помощью инструмента анализа данных Регрессия:
1) запишите статистические данные в ячейки листа Excel;
2) в главном меню выберете Сервис/Анализ данных/Регрессия. Щелкните по кнопке ОК;
3) заполните диалоговое окно ввода данных и параметров вывода (рис 2.1):

Рис. 2.1 - Диалоговое окно ввода параметров инструмента Регрессия
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал Х – диапазон, содержащий данные факторов независимого признака;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
Новый рабочий лист – можно задать произвольное имя нового листа.
Чтобы получить информацию и графики остатков, установите соответствующие флажки в диалоговом окне. Щелкните по кнопке ОК.

Рис. 2.2 - Результат применения инструмента Регрессия
Столбец Коэффициенты содержит численные значения коэффициентов регрессии:
![]() .
.
При увеличении торговой площади на 1 тыс. м2 годовой товарооборот увеличится на 61,6583 млн. руб. При увеличении среднего числа посетителей на 1 тыс. чел. годовой товарооборот увеличится на 2,2748 млн. руб.
2. Уравнение в стандартизированном масштабе имеет вид:
![]() .
.
Расчет β-коэффициентов
выполним, используя формулы для перехода
от βi
к bi:
![]() .
.
![]()
Получим уравнение
![]() .
.
3. Для характеристики относительной силы влияния x1 и x2 на y рассчитаем средние коэффициенты эластичности:
![]()
С увеличением торговой площади x1 на 1% от ее среднего уровня годовой товарооборот y возрастает на 0,8% от своего среднего уровня; при повышении среднего числа посетителей в день х2 на 1% годовой товарооборот y возрастает на 0,35% от своего среднего уровня. Очевидно, что сила влияния торговой площади на годовой товарооборот оказалась большей, чем сила влияния среднего числа посетителей в день. К аналогичным выводам о силе связи приходим при сравнении модулей значений β1 и β2.
4. Матрицу парных коэффициентов корреляции переменных можно рассчитать, используя инструмент анализа данных Корреляция. Для этого:
1) в главном меню последовательно выберете пункты Сервис/Анализ данных/Корреляция. Щелкните по кнопке ОК;
2) заполните диалоговое окно ввода данных и параметров вывода (рис 2.3);
Рис. 2.3 - Диалоговое окно ввода параметров инструмента Корреляция
3) результаты вычислений представлены на рис. 2.4.

Рис. 2.4 - Матрица коэффициентов парной корреляции
Линейные коэффициенты частной корреляции рассчитаем по формулам:



Из-за средней
межфакторной связи (![]() коэффициенты парной и частной корреляции
несколько отличаются: выводы о тесноте
и направлении связи на основе парных и
частных коэффициентов совпадают.
коэффициенты парной и частной корреляции
несколько отличаются: выводы о тесноте
и направлении связи на основе парных и
частных коэффициентов совпадают.
Значение линейного
коэффициента множественной корреляции
расположено в строке Множественный
R
таблицы
Регрессионная статистика (рис.
2.2):
![]()
Множественный
коэффициент детерминации (строка
R-квадрат):
![]()
Зависимость y от x1 и x2 характеризуется как тесная, в которой 98,8% вариации годового товарооборота определяется вариацией учтенных в модели факторов: торговой площади и среднего числа посетителей в день.
5. Задача дисперсионного анализа состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии в целом и показателя тесноты связи. Анализ выполняется при сравнении фактического и критического значений F-критерия Фишера.
Результаты дисперсионного анализа представлены в таблице Дисперсионный анализ (рис. 2.2). Столбец SS содержит суммы квадратов отклонений, столбец MS – дисперсии на одну степень свободы.
Fкр. находим по таблице значений F-критерия Фишера при уровне значимости и степенях свободы k1=2, k2=9: Fкр=4,26.
Так как Fнабл=384,2 > Fкр=4,26, гипотеза Н0 о случайности различий факторной и остаточной дисперсий отклоняется. Эти различия существенны, статистически значимы, уравнение надежно, значимо, показатель тесноты связи надежен и отражает устойчивую зависимость годового товарооборота от торговой площади и среднего числа посетителей.
С вероятностью 0,95 делаем заключение о статистической значимости уравнения в целом и показателя тесноты связи, которые сформировались под неслучайным воздействием факторов x1 и x2.
6. Частные F-критерии – Fx1 и Fx2 оценивают статистическую значимость присутствия факторов х1 и x2 в уравнении множественной регрессии, оценивают целесообразность включения в уравнение одного фактора после другого фактора.

Fкр=5,12; α=0,05.
Так как Fx1набл > Fкр, приходим к выводу о целесообразности включения в модель фактора х1 после фактора х2. Гипотезу Н0 о несущественности прироста R2y за счет включения дополнительного фактора х1 отклоняем и приходим к выводу о статистически подтвержденной целесообразности включения фактора х1 после фактора х2.

Так как Fx2набл > Fкр, гипотезу Н0 о несущественности прироста R2y за счет включения дополнительного фактора х2 отклоняем и приходим к выводу о статистически подтвержденной целесообразности включения фактора х2 после фактора х1.
7. Оценка
значимости коэффициентов b1
и b2
с помощью t-критерия
Стьюдента предполагает сопоставление
их значений с величиной их стандартных
ошибок:
![]() .
.
Значения стандартных ошибок и t-критерия Стьюдента для коэффициентов регрессии расположены в последней таблице вывода итогов построения регрессии (рис. 2.2):
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Табличное значение t-критерия Стьюдента tкр для числа степеней свободы df=12-3=9 и α=0,05 составит 2,26.
Сравнивая tкр и tнабл, приходим к выводу, что коэффициенты регрессии b1 и b2 являются статистически значимыми и надежными.
Несмотря на
полученную незначимость коэффициента
b0
(![]() ),
принято оставлять константу в уравнении
регрессии для поглощения неучтенных в
модели факторов.
),
принято оставлять константу в уравнении
регрессии для поглощения неучтенных в
модели факторов.
Интервальные значения коэффициентов регрессии составят (рис.2.2):
![]() ,
,
![]() .
.
С вероятностью 0,95 истинная сила влияния переменной х1 на у будет не меньше 55 и не больше 68,3; переменной х2 – не меньше 0,96 и не больше 3,6.
Пример 2. Имеются данные по странам (табл. 2.2).
Таблица 2.2 – Исходные данные
Страна |
Индекс человеческого развития, у |
Ожидаемая продолжительность жизни при рождении в 2000 г., лет, х1 |
Суточная калорийность питания населения, ккал на душу, х2 |
Австрия |
0,904 |
77 |
3343 |
Австралия |
0,922 |
78,2 |
3001 |
Аргентина |
0,827 |
72,9 |
3136 |
Белоруссия |
0,763 |
68 |
3101 |
Бельгия |
0,923 |
77,2 |
3543 |
Бразилия |
0,739 |
66,8 |
2938 |
Великобритания |
0,918 |
77,2 |
3237 |
Венгрия |
0,795 |
70,9 |
3402 |
Германия |
0,906 |
77,2 |
3330 |
Греция |
0,867 |
78,1 |
3575 |
Дания |
0,905 |
75,7 |
3808 |
Египет |
0,616 |
66,3 |
3289 |
Израиль |
0,883 |
77,8 |
3272 |
Индия |
0,545 |
62,6 |
2415 |
Испания |
0,894 |
78 |
3295 |
Италия |
0,9 |
78,2 |
3504 |
Канада |
0,932 |
79 |
3056 |
Казахстан |
0,74 |
67,7 |
3007 |
Китай |
0,701 |
69,8 |
2844 |
Латвия |
0,744 |
68,4 |
2861 |
Нидерланды |
0,921 |
77,9 |
3259 |
Норвегия |
0,927 |
78,1 |
3350 |
Требуется:
1. Построить уравнение множественной регрессии.
2. Провести тестирование ошибок уравнения множественной регрессии на гетероскедастичность, применив тест Гольдфельда-Квандта.
3. Определить, какое уравнение лучше использовать для прогноза: парную регрессию у от х1 или множественную регрессию.
Решение:
1. Расчет параметров линейного уравнение множественной регрессии y от x1 и x2 произведем с помощью инструмента анализа данных Регрессия.
Уравнение регрессии имеет вид:
![]() .
.
Так как Fнабл = 96,7 > Fкр = 3,52, признается статистическая значимость и надежность уравнения регрессии и показателя тесноты связи (R2=0,91).
По t-критерию
Стьюдента параметры b0
и b1
статистически значимы и существенно
отличны от нуля (![]() ).
).
Параметр b2 признается равным нулю, поскольку:
![]() .
.
2. Для оценки гетероскедастичности используем метод Гольдфельда-Квандта.
Упорядочим n = 22 наблюдений по мере возрастания переменной х1. Далее, исключив С = 6 центральных наблюдений, разобьем совокупность на две части по 8 наблюдений.
По каждой группе наблюдений находим уравнение регрессии, теоретические значения , остатки и их квадраты (табл. 2.3).
Таблица 2.3 – Проверка линейной регрессии на гетероскедастичность
Уравнение регрессии |
у |
х1 |
х2 |
|
ε |
ε2 |
|
0,545 |
62,6 |
2415 |
0,5635 |
-0,0185 |
0,00034 |
0,616 |
66,3 |
3289 |
0,6750 |
-0,0590 |
0,00348 |
|
0,739 |
66,8 |
2938 |
0,6841 |
0,0549 |
0,00301 |
|
0,74 |
67,7 |
3007 |
0,7094 |
0,0306 |
0,00094 |
|
0,763 |
68 |
3101 |
0,7188 |
0,0442 |
0,00196 |
|
0,744 |
68,4 |
2861 |
0,7266 |
0,0174 |
0,00030 |
|
0,701 |
69,8 |
2844 |
0,7644 |
-0,0634 |
0,00401 |
|
0,795 |
70,9 |
3402 |
0,8013 |
-0,0063 |
0,00004 |
|
Сумма |
|
|
|
|
|
S1=0,014084 |
|
0,883 |
77,8 |
3272 |
0,9010 |
-0,0180 |
0,00032 |
0,921 |
77,9 |
3259 |
0,9035 |
0,0175 |
0,00031 |
|
0,894 |
78 |
3295 |
0,9027 |
-0,0087 |
0,00008 |
|
0,867 |
78,1 |
3575 |
0,8851 |
-0,0181 |
0,00033 |
|
0,927 |
78,1 |
3350 |
0,9005 |
0,0265 |
0,00070 |
|
0,922 |
78,2 |
3001 |
0,9262 |
-0,0042 |
0,00002 |
|
0,9 |
78,2 |
3504 |
0,8916 |
0,0084 |
0,00007 |
|
0,932 |
79 |
3056 |
0,9355 |
-0,0035 |
0,00001 |
|
Сумма |
|
|
|
|
|
S2=0,00183 |
Находим отношение:
R = Smax/Smin
= 0,014084/0,00183 = 7,7. Сравним эту величину с
табличным значением F-критерия при
5%-ном уровне значимости и числе степеней
свободы
![]() для каждой остаточной суммы квадратов:
Fкр
= 5,05.
для каждой остаточной суммы квадратов:
Fкр
= 5,05.
Так как R > Fкр, то делаем вывод о наличии гетероскедастичности остатков. Это означает, что для каждого значения фактора х1 остатки εi имеют неодинаковую дисперсию.
3. Уравнение множественной регрессии y от x1 и x2:
![]() .
(1)
.
(1)
Построим уравнение парной линейной регрессии у от х1:
![]() .
(2)
.
(2)
Чтобы определить, какое уравнение (1) или (2) лучше использовать для прогноза, применим тест на выбор «длинной» или «короткой» регрессии.
Определим для каждого уравнения регрессии сумму квадратов ошибок:
ESSUR = 0,0229 – для «длинной» регрессии (1);
ESSR = 0,0238 – для «короткой» регрессии (2).
Вычислим F-статистику:
![]()
![]() ,
,
где q и k – число переменных х в «короткой» и «длинной» регрессии, соответственно.
Критическая точка распределения Фишера при уровне значимости 0,05: Fкр(q,n-k-1) = Fкр(1,19) = 4,38.
Так как F < Fкр, для прогноза лучше использовать «короткую» модель, т.е. уравнение регрессии (2).
2.1. Контрольные задания
Задание к задачам 1-20.
По данным об экономических результатах деятельности российских банков выполните следующие задания:
1. Построить линейное уравнение множественной регрессии и пояснить экономический смысл его параметров.
2. Определить стандартизованные коэффициенты регрессии.
3. Рассчитать частные коэффициенты эластичности, сравнить их с β1 и β2, пояснить различия между ними.
4. Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции.
5. Провести дисперсионный анализ для проверки статистической значимости уравнения множественной регрессии и его показателя тесноты связи на уровне значимости α=0,05.
6. Рассчитать частные F-критерии Фишера.
7. Оценить с помощью t-критерия Стьюдента статистическую значимость коэффициентов при переменных х1 и х2 множественного уравнения регрессии.
Задачи 1, 11
Используйте признаки: работающие активы, млн руб., собственный капитал, %, привлеченные межбанковские кредиты, %.
Задачи 2, 12
Используйте признаки: работающие активы, млн руб., собственный капитал, %, средства частных лиц, %.
Задачи 3, 13
Используйте признаки: работающие активы, млн руб., собственный капитал, %, средства предприятий и организаций, %.
Задачи 4, 14
Используйте признаки: работающие активы, млн руб., привлеченные межбанковские кредиты, %, средства предприятий и организаций, %.
Задачи 5, 15
Используйте признаки: работающие активы, млн руб., собственный капитал, %, выпущенные ценные бумаги, %.
Задачи 6, 16
Используйте признаки: работающие активы, млн руб., привлеченные межбанковские кредиты, %, выпущенные ценные бумаги, %.
Задачи 7, 17
Используйте признаки: работающие активы, млн руб., средства частных лиц, %, средства предприятий и организаций, %.
Задачи 8, 18
Используйте признаки: работающие активы, млн. руб., средства частных лиц, %, выпущенные ценные бумаги, %.
Задачи 9, 19
Используйте признаки: кредиты предприятиям и организациям, млн руб., собственный капитал, %, средства частных лиц, %.
Задачи 10, 20
Используйте признаки: кредиты предприятиям и организациям, млн руб., средства предприятий и организаций, %, выпущенные ценные бумаги, %.
Таблица 2.4 - Исходные данные
Банк |
Работающие активы, млн руб. |
Собственный капитал, % |
Привлеченные межбанковские кредиты (МБК), % |
Средства частных лиц, % |
Средства предприятий и организаций, % |
Выпущенные ценные бумаги, % |
Кредиты частным лицам, млн руб. |
Кредиты предприятиям и организациям, млн руб. |
Акции, млн руб. |
Облигации, млн руб. |
к задачам 1-10 |
||||||||||
Сбербанк |
1917403 |
10 |
3 |
60 |
19 |
3 |
308437 |
1073255 |
13571 |
359499 |
Внешторгбанк |
426484 |
16 |
28 |
13 |
25 |
12 |
5205 |
189842 |
23152 |
50012 |
Газпромбанк |
362532 |
8 |
17 |
9 |
38 |
22 |
5084 |
207118 |
18660 |
35676 |
Альфа-банк |
186700 |
13 |
14 |
15 |
30 |
3 |
1361 |
138518 |
4505 |
8471 |
Банк Москвы |
157286 |
11 |
2 |
30 |
27 |
5 |
5768 |
90757 |
3026 |
24838 |
Росбанк |
151849 |
8 |
4 |
19 |
55 |
10 |
4466 |
62388 |
4474 |
5667 |
Промстройбанк |
85365 |
10 |
13 |
24 |
29 |
11 |
2719 |
45580 |
2781 |
18727 |
Уралсиб |
76617 |
16 |
15 |
22 |
19 |
10 |
8170 |
43073 |
6705 |
4026 |
Промсвязьбанк |
54848 |
9 |
14 |
11 |
46 |
11 |
822 |
32761 |
68 |
5250 |
Петрокоммерц |
53701 |
15 |
5 |
26 |
37 |
11 |
1693 |
23053 |
3561 |
9417 |
Номос-банк |
52473 |
11 |
24 |
6 |
17 |
24 |
476 |
28511 |
2126 |
9416 |
Зенит |
50666 |
14 |
19 |
10 |
36 |
17 |
421 |
25412 |
2743 |
8264 |
Транскредитбанк |
41332 |
9 |
7 |
8 |
46 |
27 |
993 |
18506 |
827 |
7350 |
Еврофинанс-Моснарбанк |
38245 |
15 |
18 |
5 |
22 |
37 |
171 |
18114 |
400 |
7949 |
Никойл |
36946 |
23 |
27 |
11 |
23 |
9 |
245 |
13117 |
9160 |
5231 |
Импэксбанк |
34032 |
13 |
9 |
37 |
20 |
11 |
3993 |
15047 |
4098 |
2584 |
Союз |
33062 |
13 |
10 |
8 |
34 |
31 |
3254 |
15507 |
3172 |
5187 |
Татфондбанк |
11949 |
22 |
8 |
20 |
27 |
18 |
544 |
9897 |
69 |
561 |
к задачам 11-20 |
||||||||||
БИН-банк |
32948 |
12 |
4 |
20 |
35 |
11 |
764 |
24980 |
17 |
2172 |
Россельхозбанк |
23863 |
21 |
10 |
14 |
23 |
29 |
1178 |
13953 |
102 |
1628 |
Собинбанк |
20905 |
25 |
7 |
15 |
24 |
19 |
1680 |
15405 |
18 |
322 |
Судостроительный банк |
18991 |
16 |
20 |
2 |
24 |
16 |
179 |
6811 |
20 |
950 |
Банк Санкт-Петербург |
18389 |
10 |
3 |
28 |
38 |
10 |
240 |
11911 |
140 |
2862 |
Авангард |
16070 |
19 |
22 |
12 |
19 |
21 |
727 |
11839 |
718 |
227 |
Кредитагропромбанк |
15332 |
9 |
2 |
14 |
46 |
21 |
3153 |
5334 |
40 |
622 |
Инвестсбербанк |
15326 |
17 |
4 |
26 |
34 |
16 |
3085 |
6249 |
814 |
1192 |
Пробизнесбанк |
13026 |
12 |
10 |
9 |
29 |
22 |
548 |
6913 |
794 |
680 |
Российский капитал |
10249 |
30 |
4 |
21 |
27 |
11 |
899 |
6971 |
51 |
484 |
БИН-банк |
32948 |
12 |
4 |
20 |
35 |
11 |
764 |
24980 |
17 |
2172 |
Россельхозбанк |
23863 |
21 |
10 |
14 |
23 |
29 |
1178 |
13953 |
102 |
1628 |
Собинбанк |
20905 |
25 |
7 |
15 |
24 |
19 |
1680 |
15405 |
18 |
322 |
Судстрой банк |
18990 |
16 |
20 |
2 |
24 |
16 |
179 |
6811 |
20 |
950 |
Банк Петербург |
18390 |
10 |
3 |
28 |
38 |
10 |
240 |
11911 |
140 |
2862 |
МБСП |
11889 |
13 |
8 |
13 |
46 |
14 |
295 |
5404 |
12 |
4676 |
Абсолют банк |
11831 |
12 |
29 |
10 |
21 |
17 |
639 |
7872 |
40 |
413 |
Центрокредит |
11674 |
29 |
8 |
5 |
29 |
13 |
364 |
5097 |
864 |
3438 |
3. Системы эконометрических уравнений
Сложные экономические процессы описывают с помощью системы взаимосвязанных (одновременных) уравнений.
Различают несколько видов систем уравнений:
1. система независимых уравнений – когда каждая зависимая переменная y рассматривается как функция одного и того же набора факторов x:

2. система рекурсивных уравнений – когда зависимая переменная y одного уравнения выступает в виде фактора x в другом уравнении:

Для решения этой системы и нахождения ее параметров используется метод наименьших квадратов.
3. система взаимосвязанных уравнений - когда одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других - в правую:

Такая система уравнений называется структурной формой модели (СФМ).
Эндогенные переменные – взаимозависимые переменные, которые определяются внутри модели (системы) y.
Экзогенные переменные – независимые переменные, которые определяются вне системы x.
Предопределенные переменные – экзогенные и лаговые (за предшествующие моменты времени эндогенные переменные системы).
Коэффициенты a и b при переменных – структурные коэффициенты модели.
Система линейных функций эндогенных переменных от всех предопределенных переменных системы – приведенная форма модели (ПФМ):
![]()
где δ – коэффициенты приведенной формы модели.
С позиции идентифицируемости структурные модели можно подразделить на три вида: идентифицируемые, неидентифицируемые и сверхидентифицируемые.
Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров ПФМ.
Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели.
Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента.
Необходимое условие идентификации – выполнение счетного правила:
D+1=H – уравнение идентифицируемо;
D+1<H – уравнение неидентифицируемо;
D+1>H – уравнение сверхидентифицируемо,
где H – число эндогенных переменных в уравнении,
D – число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе.
Достаточное условие идентификации – определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в исследуемом уравнении, не равен нулю, и ранг этой матрицы не менее числа эндогенных переменных системы без единицы.
Выполнение условия идентифицируемости модели проверяется для каждого уравнения системы.
Для решения идентифицируемого уравнения применяется косвенный метод наименьших квадратов, для решения сверхидентифицируемых – двухшаговый метод наименьших квадратов.
Косвенный метод наименьших квадратов состоит в следующем:
составляют приведенную форму модели и определяют численные значения параметров каждого ее уравнения обычным МНК;
путем алгебраических преобразований переходят от приведенной формы модели к уравнениям структурной формы модели, получая тем самым численные оценки структурных параметров.
3.1. Решение типовых задач
Пример 1.
Требуется:
1. Оценить следующую структурную модель на идентификацию:

2. Исходя из приведенной формы модели уравнений

найти структурные коэффициенты модели.
Решение:
1. Модель имеет три эндогенные (y1, y2, y3) и три экзогенные (x1, x2, x3) переменные.
Проверим каждое уравнение системы на необходимое (Н) и достаточное (Д) условия идентификации.
Первое уравнение.
Н: эндогенных переменных – 2 (y1, y3),
отсутствующих экзогенных – 1 (x2).
Выполняется необходимое равенство: 2=1+1, следовательно, уравнение точно идентифицируемо.
Д: в первом уравнении отсутствуют y2 и x2. Построим матрицу из коэффициентов при них в других уравнениях системы:
Уравнение |
Отсутствующие переменные |
|
y2 |
x2 |
|
Второе |
-1 |
a22 |
Третье |
b32 |
0 |
![]()
Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и первое уравнение точно идентифицируемо.
Второе уравнение.
Н: эндогенных переменных – 3 (y1, y2, y3),
отсутствующих экзогенных – 2 (x1, x3).
Выполняется необходимое равенство: 3=2+1, следовательно, уравнение точно идентифицируемо.
Д: во втором уравнении отсутствуют x1 и x3. Построим матрицу из коэффициентов при них в других уравнениях системы:
Уравнение |
Отсутствующие переменные |
|
x1 |
x3 |
|
Первое |
a11 |
a13 |
Третье |
a31 |
a33 |
![]()
Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и второе уравнение точно идентифицируемо.
Третье уравнение.
Н: эндогенных переменных – 2 (y2, y3),
отсутствующих экзогенных – 1 (x2).
Выполняется необходимое равенство: 2=1+1, следовательно, уравнение точно идентифицируемо.
Д: в третьем уравнении отсутствуют y1 и x2. Построим матрицу из коэффициентов при них в других уравнениях системы:
Уравнение |
Отсутствующие переменные |
|
y1 |
x2 |
|
Первое |
-1 |
0 |
Третье |
b21 |
a22 |
![]()
Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и третье уравнение точно идентифицируемо.
Следовательно, исследуемая система точно идентифицируема и может быть решена косвенным методом наименьших квадратов.
2. Вычислим структурные коэффициенты модели:
1) из третьего уравнения приведенной формы выразим x2 (так как его нет в первом уравнении структурной формы):
![]()
Данное выражение содержит переменные y3, x1 и x3, которые нужны для первого уравнения СФМ. Подставим полученное выражение x2 в первое уравнение ПФМ:
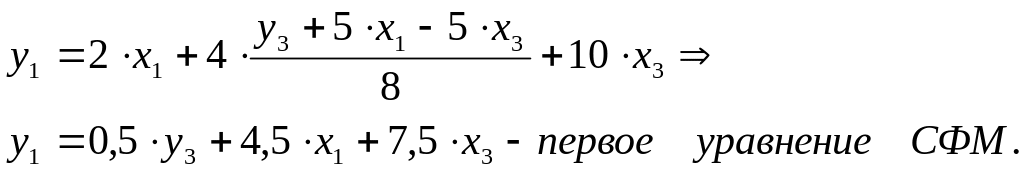
2) во втором уравнении СФМ нет переменных x1 и x3. Структурные параметры второго уравнения СФМ можно будет определить в два этапа:
Первый этап: выразим x1 в данном случае из первого или третьего уравнения ПФМ. Например, из первого уравнения:
![]()
Подстановка данного выражения во второе выражение ПФМ не решило бы задачу до конца, так как в выражении присутствует x3, которого нет в СФМ.
Выразим x3 из третьего уравнения ПФМ:
![]()
Подставим его в выражение x1:
![]()
![]()
Второй этап: аналогично, чтобы выразить x3 через искомые y1, y3 и x2, заменим в выражении x3 значение x1 на полученное из первого уравнения ПФМ:
![]()
Следовательно,
![]()
Подставим полученные x1 и x3 во второе уравнение ПФМ:
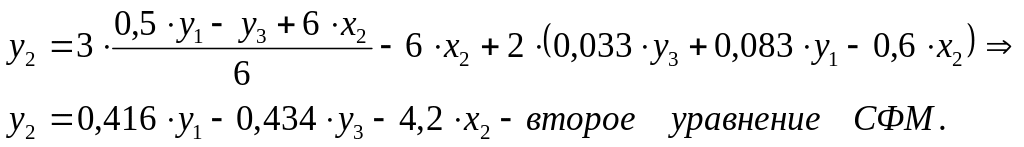
3) из второго уравнения ПФМ выразим x2, так как его нет в третьем уравнении СФМ:
![]()
Подставим полученное выражение в третье уравнение ПФМ:
![]()
Таким образом, СФМ примет вид:

Пример 2. Имеются данные за 5 лет (табл. 3.1).
Таблица 3.1 – Исходные данные
Номер года |
Годовое потребление свинины на душу населения, фунтов, у1 |
Оптовая цена за фунт, долл., у2 |
Доход на душу населения, долл., х1 |
Расходы по обработке мяса, % к цене, х2 |
1 |
60 |
5,0 |
1300 |
60 |
2 |
62 |
4,0 |
1300 |
56 |
3 |
65 |
4,2 |
1500 |
56 |
4 |
62 |
5,0 |
1600 |
63 |
5 |
66 |
3,8 |
1800 |
50 |
Требуется:
Построить модель вида
![]()
рассчитав соответствующие структурные коэффициенты.
Решение:
Система одновременных уравнений с двумя эндогенными и двумя экзогенными переменными имеет вид
![]()
В каждом уравнении две эндогенные и одна отсутствующая экзогенная переменная из имеющихся в системе. Для каждого уравнения данной системы действует счетное правило 2 = 1+1. Это означает, что каждое уравнение и система в целом идентифицированы.
Для определения параметров такой системы применяется косвенный метод наименьших квадратов.
С этой целью структурная форма модели преобразуется в приведенную форму:
![]()
в которой коэффициенты при х определяются методом наименьших квадратов.
Для нахождения значений δ11 и δ12 запишем систему нормальных уравнений:

При ее решении предполагается, что х и у выражены через отклонения от средних уровней, т.е. матрица исходных данных составит:


Применительно к ней необходимые суммы оказываются следующими:
![]()
Система нормальных уравнений составит:
![]()
Решая ее, получим:
![]()
Первое уравнение
ПФМ:
![]() .
.
Аналогично строим систему нормальных уравнений для определения коэффициентов δ21 и δ22:

![]()
![]()
Следовательно,
![]()
Второе уравнение
ПФМ:
![]() .
.
Приведенная форма модели имеет вид:
![]()
из чего определяем коэффициенты структурной модели:

![]()

![]()
Структурная форма модели имеет вид:
![]()
3.2. Контрольные задания
Задание к задачам 1-20.
Имеются структурная модель и приведенная форма модели (таблица 3.1).
Требуется:
1. Проверить структурную модель на необходимое и достаточное условия идентификации;
2. Исходя из приведенной формы модели уравнений, найти структурные коэффициенты модели.
Таблица 3.2 – Исходные данные
Вариант |
Структурная модель |
Приведенная форма |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
продолжение таблицы 3.1
Вариант |
Структурная модель |
Приведенная форма |
5 |
|
|
6 |
|
|
7 |
|
|
8
|
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
продолжение таблицы 3.2
Вариант |
Структурная модель |
Приведенная форма |
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
4. Временные ряды
Временной ряд – это совокупность значений какого либо показателя за несколько последовательных моментов или периодов времени.
Данные, представленные в виде временных рядов, могут содержать два вида компонент — систематическую и случайную составляющие. Систематическая составляющая является результатом влияния постоянно действующих факторов. Выделяют три основных систематических компоненты временного ряда:
1) Тренд — это систематическая линейная или нелинейная компонента, плавно изменяющая во времени (Т). Он описывает чистое влияние долговременных факторов.
2) Циклическая (сезонная) компонента (S). Сезонность — это периодические колебания уровней временного ряда в течение не очень длительного периода (недели, месяца, максимум — года). Цикличность отражает повторяемость экономических процессов в течение длительных периодов.
Систематические составляющие могут одновременно присутствовать во временном ряду.
Случайной составляющей называется случайный шум, или ошибка, воздействующая на временной ряд нерегулярно (E). Основными причинами случайного шума могут быть факторы резкого и внезапного воздействия , а также воздействие текущих факторов, которое может быть связано, например, с ошибками наблюдений.
Модель, в которой временной ряд представлен как сумма перечисленных компонент, называется аддитивной моделью временного ряда (Y=T+S+E). Модель, в которой временной ряд представлен как произведение перечисленных компонент, называется мультипликативной моделью временного ряда (Y=T∙S∙E).
Выбор одной из двух моделей проводится на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.
При наличии тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих значений. Корреляционную зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней ряда.
Количественно ее можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда yt и уровнями этого ряда, сдвинутыми на несколько шагов во времени yt-.
Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается. Максимальный лаг должен быть не больше (n/4).
Коэффициент автокорреляции уровней ряда первого порядка, измеряющий зависимость между соседними уровнями ряда yt и yt-1, т.е. при лаге 1, рассчитывается по формуле:
 ,
,
где

Аналогично определяются коэффициенты автокорреляции второго и более высоких порядков. Так, коэффициент автокорреляции второго порядка характеризует тесноту связи между уровнями yt и yt-2 и определяется по формуле:
 ,
,
где

Коэффициент автокорреляции характеризует тесноту только линейной связи текущего и анализируемого уровней ряда. Поэтому по коэффициенту автокорреляции можно судить о наличии линейной (или близкой к линейной) тенденции. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (например, параболу или экспоненту), коэффициент автокорреляции уровней исходного ряда может приближаться к нулю.
Последовательность коэффициентов автокорреляции уровней первого, второго и т. д. порядков называют автокорреляционной функцией временного ряда. График зависимости ее значений от величины лага называется коррелограммой.
При помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда.
Анализ структуры можно проводить следующим образом:
если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только тенденцию;
если наиболее высоким оказался коэффициент автокорреляции порядка τ, ряд содержит циклические колебания с периодичностью в τ моментов времени;
если ни один из коэффициентов автокорреляции не является значимым, можно сделать одно из предположений относительно структуры ряда:
ряд не содержит тенденции и циклических колебаний, а включает только случайную компоненту,
ряд содержит сильную нелинейную тенденцию.
Построение аналитической функции для моделирования тенденции (тренда) временного ряда называют аналитическим выравниванием временного ряда. Для этого чаще всего применяются следующие функции:
линейная
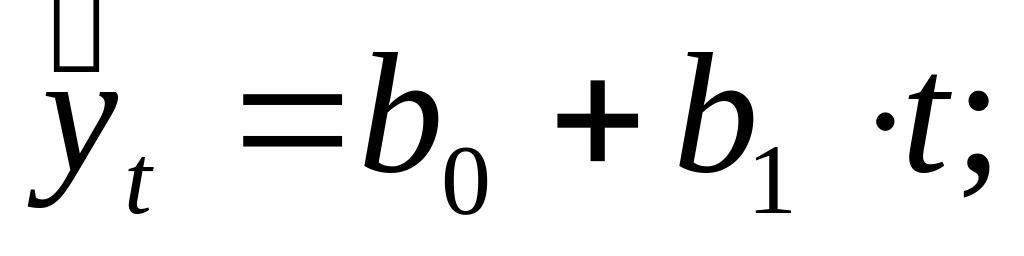
гипербола

экспонента

степенная функция

парабола второго и более высоких порядков

Параметры трендов определяются обычным МНК, в качестве независимой переменной выступает время t=1, 2,…, n, а в качестве зависимой переменной – фактические уровни временного ряда yt.
Построение аддитивной и мультипликативной моделей сводится к расчету значений Т, S и Е для каждого уровня ряда. Процесс построения модели включает в себя следующие шаги.
1) Выравнивание исходного ряда методом скользящей средней.
2) Расчет значений сезонной компоненты S.
3) Устранение сезонной компоненты из исходных уровней ряда и получение выравненных данных (Т+Е) в аддитивной или (Т∙Е) в мультипликативной модели.
4) Аналитическое выравнивание уровней (Т+Е) или (Т∙Е) и расчет значений Т с использованием полученного уравнения тренда.
5) Расчет полученных по модели значений (Т+S) или (Т∙S).
6) Расчет абсолютных и/или относительных ошибок.
Автокорреляция в остатках – корреляционная зависимость между значениями остатков εt за текущий и предыдущие моменты времени.
Для определения автокорреляции остатков используют критерий Дарбина-Уотсона и расчет величины:

Выдвигается гипотеза Н0 об отсутствии автокорреляции остатков. Альтернативные гипотезы Н1 и Н1* состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках.
Далее по специальным таблицам определяются критические значения критерия Дарбина-Уотсона dL и dU для заданного числа наблюдений n, числа независимых переменных модели k и уровня значимости α. По этим значениям числовой промежуток [0;4] разбивают на пять отрезков.
Принятие или отклонение каждой из гипотез с вероятностью (1-α) рассматривается на рис. 4.1.

0 dL dU 2 4-dL 4-dU 4
Рис. 4.1. – Схема проверки гипотезы о наличии автокорреляции
остатков
4.1. Решение типовых задач
Пример 1. Динамика выпуска продукции Финляндии характеризуется данными (млн. долл), представленными в табл. 4.1.
Таблица 4.1 – Исходные данные
Год |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
Выпуск продукции |
14150 |
14004 |
13088 |
12518 |
13471 |
13617 |
16356 |
20037 |
21748 |
23298 |
16570 |
23080 |
23981 |
23446 |
29658 |
38435 |
Требуется:
1. Провести расчет параметров параболического тренда. Построить графики ряда динамики и тренда.
2. Рассчитать критерий Дарбина-Уотсона. Оценить полученный результат при 5%-ном уровне значимости.
Решение:
1.
Параболический тренд имеет вид:
![]() .
.
Определение параметров тренда и построение графиков осуществим с помощью «Мастера диаграмм»:
1) введите исходные данные в ячейки листа ПП Excel;
2) на панели инструментов Стандартная щелкните по кнопке Мастер диаграмм;
3) в окне «Тип диаграммы» из списка типов выберете График; вид графика – первый из списка.
4) в окне «Источник данных диаграммы» закладка Диапазон данных заполните поле Диапазон (в нашем примере – Лист1!$A$1:$B$17); закладка Ряд заполните поле Подписи оси Х (в нашем примере – Лист1!$A$2:$A$17);
5) в окне «Параметры диаграммы» заполните параметры диаграммы на разных закладках;
6) в окне «Размещение диаграммы» укажите место размещения диаграммы;
7) после построения графика ряда динамики щелкните ПКМ на линии графика и в контекстном меню выберете Добавить линию тренда;
8) в диалоговом окне «Линия тренда» выберете вид линии тренда и задайте соответствующие параметры (рис. 4.2);
9) на рис. 4.3 представлены результаты построения графиков ряда динамики и параболического тренда.
Получили уравнение параболического тренда:
![]() .
.

Рис. 4.2 - Диалоговое окно параметров линии тренда
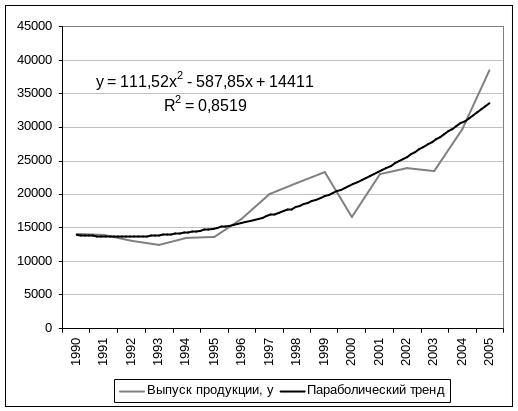
Рис. 4.3 - Графики ряда динамики и параболического тренда
2.
Выровненные
значения ряда динамики
![]() определим
путем подстановки фактических значений
t
(порядковый
номер года)
в уравнение
тренда:
определим
путем подстановки фактических значений
t
(порядковый
номер года)
в уравнение
тренда:
![]()
Остатки
εt
рассчитываются по формуле
![]()
εt-1 – те же значения, что и εt, но со сдвигом на один год.
Результаты вычислений оформим в табл.4.2.
Критерий Дарбина-Уотсона рассчитаем по формуле:

Таблица 4.2 – К расчету критерия Дарбина-Уотсона
№ |
|
εt |
εt-1 |
(εt- εt-1) |
(εt- εt-1)2 |
|
1 |
13934,7 |
215,3 |
- |
- |
- |
46367 |
2 |
13681,4 |
322,6 |
215,3 |
107,3 |
11511 |
104084 |
3 |
13651,1 |
-563,1 |
322,6 |
-885,8 |
784553 |
317115 |
4 |
13843,9 |
-1325,9 |
-563,1 |
-762,8 |
581849 |
1758064 |
5 |
14259,8 |
-788,8 |
-1325,9 |
537,2 |
288552 |
622127 |
6 |
14898,6 |
-1281,6 |
-788,8 |
-492,9 |
242921 |
1642550 |
7 |
15760,5 |
595,5 |
-1281,6 |
1877,1 |
3523467 |
354585 |
8 |
16845,5 |
3191,5 |
595,5 |
2596,1 |
6739476 |
10185800 |
9 |
18153,5 |
3594,5 |
3191,5 |
403,0 |
162417 |
12920646 |
10 |
19684,5 |
3613,5 |
3594,5 |
19,0 |
360 |
13057382 |
11 |
21438,6 |
-4868,6 |
3613,5 |
-8482,1 |
71945511 |
23702974 |
12 |
23415,7 |
-335,7 |
-4868,6 |
4532,9 |
20547092 |
112681 |
13 |
25615,8 |
-1634,8 |
-335,7 |
-1299,2 |
1687791 |
2672669 |
14 |
28039,0 |
-4593,0 |
-1634,8 |
-2958,2 |
8750888 |
21095833 |
15 |
30685,3 |
-1027,3 |
-4593,0 |
3565,8 |
12714716 |
1055243 |
16 |
33554,5 |
4880,5 |
-1027,3 |
5907,7 |
34901274 |
23819085 |
Итого |
317462,3 |
-5,3 |
-4885,8 |
4665,2 |
162882376 |
113467203
|
Фактическое значение d сравниваем с табличными значениями при 5%-ном уровне значимости. При n=16 лет и k=1 (число факторов) нижнее значение dL равно 1,1, а верхнее dU – 1,37. С вероятностью 0,95 принимается гипотеза Н0 и можно считать, что автокорреляция в остатках отсутствует. Следовательно, уравнение регрессии может быть использовано для прогноза.
Пример 2. Динамика урожайности зерновых культур за 1996-2006 гг. характеризуется данными (ц/га), представленными в табл. 4.3.
Таблица 4.3 - Урожайность зерновых культур за 1992-2006 гг.
Год |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
Урожайность, ц/га |
15,4 |
20,1 |
12 |
5,9 |
8,8 |
14,8 |
4,7 |
7 |
12,2 |
17 |
16,1 |
15,2 |
19,2 |
18,4 |
17,3 |
Требуется:
1. Построить автокорреляционную функцию временного ряда.
2. Охарактеризовать структуру этого ряда.
Решение:
1. Расчет коэффициента автокорреляции первого порядка для временного ряда урожайности зерновых культур произведем в таблице 4.4.
Таблица 4.4 - Расчет коэффициента автокорреляции первого порядка
t |
|
|
|
|
|
|
|
1 |
15,4 |
- |
- |
- |
- |
- |
- |
2 |
20,1 |
15,4 |
6,62 |
2,06 |
13,621 |
43,8433 |
4,2318 |
3 |
12 |
20,1 |
-1,48 |
6,76 |
-9,991 |
2,1862 |
45,6590 |
4 |
5,9 |
12 |
-7,58 |
-1,34 |
10,177 |
57,4347 |
1,8033 |
5 |
8,8 |
5,9 |
-4,68 |
-7,44 |
34,822 |
21,8890 |
55,3961 |
6 |
14,8 |
8,8 |
1,32 |
-4,54 |
-6,003 |
1,7462 |
20,6376 |
7 |
4,7 |
14,8 |
-8,78 |
1,46 |
-12,792 |
77,0633 |
2,1233 |
8 |
7 |
4,7 |
-6,48 |
-8,64 |
55,993 |
41,9719 |
74,6990 |
9 |
12,2 |
7 |
-1,28 |
-6,34 |
8,110 |
1,6347 |
40,2318 |
10 |
17 |
12,2 |
3,52 |
-1,14 |
-4,024 |
12,4005 |
1,3061 |
11 |
16,1 |
17 |
2,62 |
3,66 |
9,587 |
6,8719 |
13,3747 |
12 |
15,2 |
16,1 |
1,72 |
2,76 |
4,746 |
2,9633 |
7,6018 |
13 |
19,2 |
15,2 |
5,72 |
1,86 |
10,626 |
32,7347 |
3,4490 |
14 |
18,4 |
19,2 |
4,92 |
5,86 |
28,826 |
24,2205 |
34,3061 |
15 |
17,3 |
18,4 |
3,82 |
5,06 |
19,326 |
14,6033 |
25,5747 |
Итого |
188,7* |
186,8 |
0,00 |
0,00 |
163,023 |
341,5636 |
330,3943 |
*) Сумма приведена без значения 15,4 (затемненная ячейка).
Средние
![]() составят:
составят:

Коэффициент автокорреляции первого порядка:
![]()
Полученное значение свидетельствует об отсутствии зависимости между урожайностью зерновых культур текущего и непосредственно предшествующего годов.
Расчет коэффициента автокорреляции второго порядка для временного ряда урожайности зерновых культур произведем в таблице 4.5.
Таблица 4.5 - Расчет коэффициента автокорреляции второго порядка
t |
|
|
|
|
|
|
|
1 |
15,4 |
- |
- |
- |
- |
- |
- |
2 |
20,1 |
- |
- |
- |
- |
- |
- |
3 |
12 |
15,4 |
-0,97 |
2,45 |
-2,371 |
0,9394 |
5,9837 |
4 |
5,9 |
20,1 |
-7,07 |
7,15 |
-50,518 |
49,9740 |
51,0675 |
5 |
8,8 |
12 |
-4,17 |
-0,95 |
3,977 |
17,3825 |
0,9098 |
6 |
14,8 |
5,9 |
1,83 |
-7,05 |
-12,914 |
3,3517 |
49,7567 |
7 |
4,7 |
8,8 |
-8,27 |
-4,15 |
34,349 |
68,3802 |
17,2544 |
8 |
7 |
14,8 |
-5,97 |
1,85 |
-11,020 |
35,6317 |
3,4083 |
9 |
12,2 |
4,7 |
-0,77 |
-8,25 |
6,349 |
0,5917 |
68,1260 |
10 |
17 |
7 |
4,03 |
-5,95 |
-23,999 |
16,2471 |
35,4483 |
11 |
16,1 |
12,2 |
3,13 |
-0,75 |
-2,360 |
9,8017 |
0,5683 |
12 |
15,2 |
17 |
2,23 |
4,05 |
9,026 |
4,9763 |
16,3714 |
13 |
19,2 |
16,1 |
6,23 |
3,15 |
19,603 |
38,8225 |
9,8983 |
14 |
18,4 |
15,2 |
5,43 |
2,25 |
12,198 |
29,4933 |
5,0452 |
15 |
17,3 |
19,2 |
4,33 |
6,25 |
27,051 |
18,7556 |
39,0144 |
Итого |
168,6* |
168,4 |
0,00 |
0,00 |
9,372 |
294,3477 |
302,8523 |
*) Сумма приведена без значений 15,4 и 20,1 (затемненные ячейки).
Средние
![]() составят:
составят:

Коэффициент автокорреляции второго порядка:
![]()
Коэффициенты автокорреляции третьего и четвертого порядков рассчитаем в среде Excel с помощью функции КОРРЕЛ при соответствующем выборе диапазона значений.
Получаем r3=0,115 и r4=0,251.
Построим автокорреляционную функцию и коррелограмму временного ряда (табл. 4.6).
Таблица 4.6 - Автокорреляционная функция и коррелограмма ВР
Лаг |
Коэффициент автокорреляции уровней |
Коррелограмма |
1 |
0,485 |
***** |
2 |
0,031 |
* |
3 |
0,115 |
* |
4 |
0,251 |
*** |
При анализе временного ряда урожайности зерновых культур наиболее высоким оказался коэффициент автокорреляции уровней первого порядка. Следовательно, исследуемый ряд содержит только тенденцию.
Пример 3. Построить аддитивную модель временного ряда потребления электроэнергии жителями города за 18 кварталов, yt (табл. 4.7).
Таблица 4.7 – Потребление электроэнергии жителями города, млн. кВт∙ч
Номер квартала |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
yt |
30 |
22 |
25 |
45 |
36 |
24 |
30 |
50 |
48 |
28 |
32 |
55 |
45 |
33 |
35 |
54 |
42 |
30 |
Решение:
Анализ значений автокорреляционной функции (АКФ) и коррелограммы (табл. 4.8) позволяет сделать вывод о наличии в изучаемом временном ряде линейной тенденции и сезонных колебаний периодичностью в четыре квартала.
Таблица 4.8 – АКФ и коррелограмма временного ряда потребления электроэнергии
Лаг |
Коэффициенты автокорреляции уровней |
Коррелограмма |
1 |
0,1802 |
** |
2 |
0,6115 |
****** |
3 |
0,1237 |
* |
4 |
0,919 |
********* |
5 |
0,0884 |
* |
6 |
0,7718 |
******** |
7 |
0,0208 |
|
8 |
0,8171 |
******** |
9 |
0,0698 |
* |
Объемы потребления электроэнергии в осенне-зимний период времени (I и IV кварталы) выше, чем весной и летом (II и III кварталы).
По графику этого ВР (рис. 4.4) можно установить наличие приблизительно равной амплитуды колебаний. Это свидетельствует о возможном существовании аддитивной модели временного ряда. Рассчитаем ее компоненты.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:
1) просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объемы потребления электроэнергии (гр.3 табл. 4.9);
2) разделив полученные суммы на 4, найдем скользящие средние (гр.4 табл. 4.9). Полученные таким образом выравненные значения уже не содержат сезонной компоненты;
3) приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних, т.е. центрированные скользящие средние (гр.5 табл. 4.9).
Таблица 4.9 – Расчет оценок сезонной компоненты в аддитивной модели
№ квартала, t |
Потребление электроэнергии, yt |
Итого по 4 кварталам |
Скользящая средняя по кварталам |
Центрированная скользящая средняя |
Оценка сезонной компоненты |
1 |
30 |
|
|
|
|
2 |
22 |
122 |
30,50 |
|
|
3 |
25 |
128 |
32,00 |
31,250 |
-6,250 |
4 |
45 |
130 |
32,50 |
32,250 |
12,750 |
5 |
36 |
135 |
33,75 |
33,125 |
2,875 |
6 |
24 |
140 |
35,00 |
34,375 |
-10,375 |
7 |
30 |
152 |
38,00 |
36,500 |
-6,500 |
8 |
50 |
156 |
39,00 |
38,500 |
11,500 |
9 |
48 |
158 |
39,50 |
39,250 |
8,750 |
10 |
28 |
163 |
40,75 |
40,125 |
-12,125 |
11 |
32 |
160 |
40,00 |
40,375 |
-8,375 |
12 |
55 |
165 |
41,25 |
40,625 |
14,375 |
13 |
45 |
168 |
42,00 |
41,625 |
3,375 |
14 |
33 |
167 |
41,75 |
41,875 |
-8,875 |
15 |
35 |
164 |
41,00 |
41,375 |
-6,375 |
16 |
54 |
161 |
40,25 |
40,625 |
13,375 |
17 |
42 |
|
|
|
|
18 |
30 |
|
|
|
|
Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (гр.6 табл. 4.9).
Найдем (табл. 4.10) средние за каждый квартал (по всем годам) оценки сезонной компоненты Si.
Таблица 4.10 – Расчет значений сезонной компоненты
в аддитивной модели
Показатели |
№ квартала, i |
|||
I |
II |
III |
IV |
|
Сезонная компонента 1-го года |
- |
- |
-6,250 |
12,750 |
Сезонная компонента 2-го года |
2,875 |
-10,375 |
-6,500 |
11,500 |
Сезонная компонента 3-го года |
8,750 |
-12,125 |
-8,375 |
14,375 |
Сезонная компонента 4-го года |
3,375 |
-8,875 |
-6,375 |
13,375 |
Итого за i-й квартал (за все годы) |
15,000 |
-31,375 |
-27,500 |
52,000 |
Средняя оценка сезонной компоненты для
i-гo
квартала,
|
5,000 |
-10,458 |
-6,875 |
13,000 |
Скорректированная сезонная компонента, Si |
4,833 |
-10,625 |
-7,041 |
12,833 |
В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимно погашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
Для данной модели
имеем:
![]() .
.
Определим корректирующий коэффициент:
![]() .
.
Рассчитаем
скорректированные значения сезонной
компоненты как разность между ее средней
оценкой и корректирующим коэффициентом
k
(![]() ).
Проверим условие равенства нулю суммы
значений сезонной компоненты:
).
Проверим условие равенства нулю суммы
значений сезонной компоненты:
![]() .
.
Таким образом, получены следующие значения сезонной компоненты по кварталам года:
S1 = 4,833; S2 = -10,625; S3 = -7,041; S4 = 12,833.
Занесем полученные значения в табл. 4.11 для соответствующих кварталов каждого года (гр. 3).
Таблица 4.11 – Расчет выровненных значений тренда и ошибок
в аддитивной модели
t |
yt |
Si |
T+E=yt – Si |
T |
T+S |
E=yt – (T+S) |
E2 |
1 |
30 |
4,833 |
25,167 |
30,756 |
35,589 |
-5,589 |
31,237 |
2 |
22 |
10,625 |
32,625 |
31,515 |
20,890 |
1,110 |
1,232 |
3 |
25 |
-7,041 |
32,041 |
32,274 |
25,233 |
-0,233 |
0,054 |
4 |
45 |
12,833 |
32,167 |
33,033 |
45,866 |
-0,866 |
0,750 |
5 |
36 |
4,833 |
31,167 |
33,792 |
38,625 |
-2,625 |
6,891 |
6 |
24 |
-10,625 |
34,625 |
34,551 |
23,926 |
0,074 |
0,005 |
7 |
30 |
-7,041 |
37,041 |
35,310 |
28,269 |
1,731 |
2,996 |
8 |
50 |
12,833 |
37,167 |
36,069 |
48,902 |
1,098 |
1,206 |
9 |
48 |
4,833, |
43,167 |
36,828 |
41,661 |
6,339 |
40,183 |
10 |
28 |
-10,625 |
38,625 |
37,587 |
26,962 |
1,038 |
1,077 |
11 |
32 |
-7,041 |
39,041 |
38,346 |
31,305 |
0,695 |
0,483 |
12 |
55 |
12,833 |
42,167 |
39,105 |
51,938 |
3,062 |
9,376 |
13 |
45 |
4,833 |
40,167 |
39,864 |
44,697 |
0,303 |
0,092 |
14 |
33 |
-10,625 |
43,625 |
40,623 |
29,998 |
3,002 |
9,012 |
15 |
35 |
-7,041 |
42,041 |
41,382 |
34,341 |
0,659 |
0,434 |
16 |
54 |
12,833 |
41,167 |
42,141 |
54,974 |
-0,974 |
0,949 |
17 |
42 |
4,833 |
37,167 |
42,900 |
47,733 |
-5,733 |
32,867 |
18 |
30 |
-10,625 |
40,625 |
43,659 |
33,034 |
-3,034 |
9,205 |
Шаг 3. Элиминируем влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного ряда.
Получим величины T+E=Y– S, (гр. 4 табл. 4.11).
Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
Шаг 4. Определим компоненту Т данной модели.
Для этого проведем аналитическое выравнивание ряда (Т+Е) с помощью линейного тренда.
Результаты аналитического выравнивания следующие:
![]()
Подставляя в это
уравнение значения t = 1, ..., 18, найдем
уровни
![]() для каждого момента времени (гр. 5 табл.
4.11).
График уравнения тренда приведен на
рис. 4.4.
для каждого момента времени (гр. 5 табл.
4.11).
График уравнения тренда приведен на
рис. 4.4.

Рис.4.4 – Потребление электроэнергии жителями города
Шаг 5. Найдем значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням тренда значения сезонной компоненты для соответствующих кварталов. Графически значения (Т+S) представлены на рис. 4.4.
Шаг 6.
В соответствии с методикой построения
аддитивной модели расчет ошибки
производится по формуле
![]() .
Численные значения абсолютных ошибок
приведены в гр. 7 табл. 4.11.
.
Численные значения абсолютных ошибок
приведены в гр. 7 табл. 4.11.
Сумма квадратов абсолютных ошибок равна 148,05 (гр. 8 табл. 4.11). Общая сумма квадратов отклонений уровней ряда от его среднего уровня составляет 1867,778. Коэффициент детерминации равен R2=0,9207.
Аддитивная модель объясняет 92.07% общей вариации уровней ряда потребления электроэнергии за последние 18 кварталов.
4.2. Контрольные задания
Задачи 1-10. Динамика выпуска продукции характеризуется данными (млн. долл.), представленными в табл. 4.3.
Требуется:
1. Провести расчет параметров линейного, степенного, экспоненциального и параболического трендов.
2. Выбрать наилучший вид тренда на основании графического изображения и значения коэффициента детерминации.
3. Построить графики ряда динамики и выбранного тренда.
4. Рассчитать критерий Дарбина-Уотсона. Оценить полученный результат при 5%-ном уровне значимости.
5. Сделать прогноз ряда на два ближайших года.
Таблица 4.12 – Исходные данные по теме «Временные ряды»
Задача |
Временные ряды |
|||||||||
1 |
1961 |
1962 |
1963 |
1964 |
1965 |
1966 |
1967 |
1968 |
1969 |
1970 |
1054 |
1104 |
1149 |
1291 |
1427 |
1505 |
1513 |
1635 |
1987 |
2306 |
|
2 |
1971 |
1972 |
1973 |
1974 |
1975 |
1976 |
1977 |
1978 |
1979 |
1980 |
2367 |
2913 |
3837 |
5490 |
2202 |
6342 |
7665 |
8570 |
11172 |
14150 |
|
3 |
1981 |
1982 |
1983 |
1984 |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
14004 |
13088 |
12518 |
13471 |
13617 |
16356 |
20037 |
21748 |
23298 |
26570 |
|
4 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
23080 |
23981 |
23446 |
29658 |
39573 |
38435 |
39002 |
39020 |
40012 |
41005 |
|
5 |
1971 |
1972 |
1973 |
1974 |
1975 |
1976 |
1977 |
1978 |
1979 |
1980 |
2467 |
3013 |
3837 |
5190 |
2200 |
6340 |
7660 |
8570 |
11072 |
14050 |
|
6 |
1981 |
1982 |
1983 |
1984 |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
14000 |
13080 |
12510 |
13470 |
13610 |
16350 |
20035 |
21745 |
23295 |
26570 |
|
7 |
1961 |
1962 |
1963 |
1964 |
1965 |
1966 |
1967 |
1968 |
1969 |
1970 |
1050 |
1100 |
1150 |
1290 |
1425 |
1505 |
1515 |
1635 |
1987 |
2306 |
|
Продолжение таблицы 4.12
8 |
1971 |
1972 |
1973 |
1974 |
1975 |
1976 |
1977 |
1978 |
1979 |
1980 |
2365 |
2915 |
3840 |
5490 |
2202 |
6342 |
7663 |
8574 |
11175 |
14144 |
|
9 |
1981 |
1982 |
1983 |
1984 |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
14000 |
13091 |
12522 |
13474 |
13616 |
16354 |
20037 |
21745 |
23299 |
26572 |
|
10 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
23085 |
23980 |
23444 |
29657 |
39570 |
38435 |
39000 |
39020 |
40012 |
41010 |
|
11 |
1961 |
1962 |
1963 |
1964 |
1965 |
1966 |
1967 |
1968 |
1969 |
1970 |
1050 |
1104 |
1144 |
1291 |
1427 |
1508 |
1513 |
1635 |
1988 |
2303 |
|
12 |
1971 |
1972 |
1973 |
1974 |
1975 |
1976 |
1977 |
1978 |
1979 |
1980 |
2377 |
2923 |
3847 |
5490 |
2212 |
6342 |
7655 |
8560 |
11072 |
14150 |
|
13 |
1981 |
1982 |
1983 |
1984 |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
14104 |
13188 |
12508 |
13471 |
13617 |
16356 |
20037 |
21728 |
23278 |
26550 |
|
14 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
23180 |
23881 |
23446 |
29558 |
39573 |
38535 |
39102 |
39020 |
40112 |
41005 |
|
15 |
1971 |
1972 |
1973 |
1974 |
1975 |
1976 |
1977 |
1978 |
1979 |
1980 |
2467 |
3013 |
3837 |
5290 |
2200 |
6240 |
7660 |
8470 |
11172 |
14050 |
|
16 |
1981 |
1982 |
1983 |
1984 |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
14110 |
13080 |
12500 |
13470 |
13630 |
16550 |
20135 |
21755 |
23195 |
26550 |
|
17 |
1961 |
1962 |
1963 |
1964 |
1965 |
1966 |
1967 |
1968 |
1969 |
1970 |
1150 |
1110 |
1350 |
1490 |
1425 |
1555 |
1515 |
1635 |
1977 |
2306 |
|
18 |
1971 |
1972 |
1973 |
1974 |
1975 |
1976 |
1977 |
1978 |
1979 |
1980 |
2385 |
2915 |
3820 |
5490 |
2262 |
6342 |
7633 |
8574 |
11375 |
14144 |
|
19 |
1981 |
1982 |
1983 |
1984 |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
14025 |
13061 |
12522 |
13484 |
13416 |
16354 |
20437 |
21445 |
23229 |
26372 |
|
20 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
23085 |
23680 |
23444 |
28657 |
39570 |
35435 |
39320 |
39020 |
40312 |
41010 |
5. Контрольные вопросы по курсу
Предмет эконометрики и сущность ее методов. С какими науками она связана.
Типы данных и классы моделей.
Этапы эконометрического моделирования.
Понятие парной и множественной регрессии.
Спецификация эконометрических моделей.
Погрешность моделей.
Смысл и оценка параметров уравнения регрессии.
Метод наименьших квадратов.
Линейный коэффициент корреляции и коэффициент детерминации.
Дисперсионный анализ результатов регрессии.
Оценка значимости уравнения регрессии с помощью F-критерия Фишера.
Оценка значимости параметров уравнения регрессии и коэффициента корреляции по t-критерию Стьюдента.
Интервальная оценка параметров регрессии.
Интервальный прогноз на основе уравнения регрессии.
Нелинейная регрессия.
Оценивание коэффициентов нелинейной регрессии.
Показатели корреляции для нелинейной регрессии.
В чем смысл средней ошибки аппроксимации и как она определяется.
Определение коэффициентов эластичности по разным видам регрессионных моделей.
Предпосылки МНК. Условия Гаусса-Маркова.
Проверка 1 и 2 предпосылок МНК (графический метод).
Проверка наличия гомо- и гетероскедастичности остатков. Метод Гольдфельда-Квандта.
Проверка автокоррелированности остатков.
Линейные регрессионные модели с гетероскедастичными и автокоррелированными остатками
Спецификация модели множественной регрессии.
Мультиколлинеарность факторов и методы ее устранения.
Оценка параметров уравнения множественной регрессии.
Тест на выбор «длинной» или «короткой» регрессии.
Множественная корреляция. Коэффициенты частной корреляции.
Оценка надежности результатов множественной регрессии и корреляции.
Обобщенный метод наименьших квадратов.
Метод максимального правдоподобия.
Способы построения систем эконометрических уравнений.
Структурная и приведенная формы модели.
Проблема идентификации. Необходимое и достаточное условия идентификации.
Оценивание параметров структурной модели. КМНК и ДМНК.
Основные элементы временного ряда.
Автокорреляция уровней временного ряда и выявление его структуры.
Моделирование тенденции временного ряда.
Моделирование сезонных и циклических колебаний. Мультипликативная и аддитивная модели временного ряда.
Моделирование тенденции ВР при наличии структурных изменений. Тест Чоу.
Стационарные и нестационарные временные ряды.
Модели нестационарных временных рядов (AR, MА, ARIMA).
Библиографический список
Варюхин А.М., Панкина О.Ю., Яковлева А.В. Эконометрика: Пособие для сдачи экзамена. – М.: Юрайт-Издат, 2005. – 191 с.
Гришин А.Ф. Статистические модели в экономике / А.Ф. Гришин, С.Ф. Котов-Дарти, В.Н. Ягунов. – Ростов н/Д: «Феникс», 2005. – 344 с.
Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник / Под ред. И.И. Елисеевой. – 5-е изд., перераб. и доп. – М.: Финансы и статистика, 2006. – 656 с.
Кремер Н.Ш., Путко Б.А. Эконометрика:Учебник для вузов / Под ред. Проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2007. – 311 с.
Луговская Л.В. Эконометрика в вопросах и ответах: учеб. пособие. – М.: ТК Велби, Изд-во Проспект, 2005. – 208 с.
Орлов А.И. Эконометрика: Учебник для вузов / А.И. Орлов.- 3-е изд., перераб. и доп. – М.: Издательство «Экзамен», 2004. – 576 с.
Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2006. – 344 с.
Статистическая обработка и анализ экономических данных / А.В. Каплан [и др.]. – Ростов н/Д: Феникс, 2007. – 330 с.
Тихомиров Н.П., Дорохина Е.Ю. Эконометрика: Учебник / Н.П. Тихомиров, Е.Ю. Дорохина – М.: Издательство «Экзамен», 2003. – 512 с.
Тюрин Ю.Н. , Макаров А.А. Анализ данных на компьютере / Под ред. В.Э. Фигурнова. – 3-е изд., перераб. и доп. – М.: ИНФРА-М, 2003. – 544 с.
Приложение 1
Таблица значений F-критерия Фишера при уровне значимости а = 0,05
k2 |
1 |
2 |
3 |
4 |
5 |
6 |
8 |
12 |
24 |
∞ |
1 |
161,45 |
199,50 |
215,72 |
224,57 |
230,17 |
233,97 |
238,89 |
243,91 |
249,04 |
254,32 |
2 |
18,51 |
19,00 |
19,16 |
19,25 |
19,30 |
19,33 |
19,37 |
19,41 |
19,45 |
19,50 |
3 |
10,13 |
9,55 |
9,28 |
9,12 |
9,01 |
8,94 |
8,84 |
8,74 |
8,64 |
8,53 |
4 |
7,71 |
6,94 |
6,59 |
6,39 |
6,26 |
6,16 |
6,04 |
5,91 |
5,77 |
5,63 |
5 |
6,61 |
5,79 |
5,41 |
5,19 |
5,05 |
4,95 |
4,82 |
4,68 |
4,53 |
4,36 |
6 |
5,99 |
5,14 |
4,76 |
4,53 |
4,39 |
4,28 |
4,15 |
4,00 |
3,84 |
3,67 |
7 |
5,59 |
4,74 |
4,35 |
4,12 |
3,97 |
3,87 |
3,73 |
3,57 |
3,41 |
3,23 |
8 |
5,32 |
4,46 |
4,07 |
3,84 |
3,69 |
3,58 |
3,44 |
3,28 |
3,12 |
2,93 |
9 |
5,12 |
4,26 |
3,86 |
3,63 |
3,48 |
3,37 |
3,23 |
3,07 |
2,90 |
2,71 |
10 |
4,96 |
4,10 |
3,71 |
3,48 |
3,33 |
3,22 |
3,07 |
2,91 |
2,74 |
2,54 |
11 |
4,84 |
3,98 |
3,59 |
3,36 |
3,20 |
3,09 |
2,95 |
2,79 |
2,61 |
2,40 |
12 |
4,75 |
3,88 |
3,49 |
3,26 |
3,11 |
3,00 |
2,85 |
2,69 |
2,50 |
2,30 |
13 |
4,67 |
3,80 |
3,41 |
3,18 |
3,02 |
2,92 |
2,77 |
2,60 |
2,42 |
2,21 |
14 |
4,60 |
3,74 |
3,34 |
3,11 |
2,96 |
2,85 |
2,70 |
2,53 |
2,35 |
2,13 |
15 |
4,54 |
3,68 |
3,29 |
3,06 |
2,90 |
2,79 |
2,64 |
2,48 |
2,29 |
2,07 |
16 |
4,49 |
3,63 |
3,24 |
3,01 |
2,85 |
2,74 |
2,59 |
2,42 |
2,24 |
2,01 |
17 |
4,45 |
3,59 |
3,20 |
2,96 |
2,81 |
2,70 |
2,55 |
2,38 |
2,19 |
1,96 |
18 |
4,41 |
3,55 |
3,16 |
2,93 |
2,77 |
2,66 |
2,51 |
2,34 |
2,15 |
1,92 |
19 |
4,38 |
3,52 |
3,13 |
2,90 |
2,74 |
2,63 |
2,48 |
2,31 |
2,11 |
1,88 |
20 |
4,35 |
3,49 |
3,10 |
2,87 |
2,71 |
2,60 |
2,45 |
2,28 |
2,08 |
1,84 |
21 |
4,32 |
3,47 |
3,07 |
2,84 |
2,68 |
2,57 |
2,42 |
2,25 |
2,05 |
1,81 |
22 |
4,30 |
3,44 |
3,05 |
2,82 |
2,66 |
2,55 |
2,40 |
2,23 |
2,03 |
1,78 |
23 |
4,28 |
3,42 |
3,03 |
2,80 |
2,64 |
2,53 |
2,38 |
2,20 |
2,00 |
1,76 |
24 |
4,26 |
3,40 |
3,01 |
2,78 |
2,62 |
2,51 |
2,36 |
2,18 |
1,98 |
1,73 |
25 |
4,24 |
3,38 |
2,99 |
2,76 |
2,60 |
2,49 |
2,34 |
2,16 |
1,96 |
1,71 |
Продолжение приложения 1
k2 |
1 |
2 |
3 |
4 |
5 |
6 |
8 |
12 |
24 |
∞ |
26 |
4,22 |
3,37 |
2,98 |
2,74 |
2,59 |
2,47 |
2,32 |
2,15 |
1,95 |
1,69 |
27 |
4,21 |
3,35 |
2,96 |
2,73 |
2,57 |
2,46 |
2,30 |
2,13 |
1,93 |
1,67 |
28 |
4,20 |
3,34 |
2,95 |
2,71 |
2,56 |
2,44 |
2,29 |
2,12 |
1,91 |
1,65 |
29 |
4,18 |
3,33 |
2,93 |
2,70 |
2,54 |
2,43 |
2,28 |
2,10 |
1,90 |
1,64 |
30 |
4,17 |
3,32 |
2,92 |
2,69 |
2,53 |
2,42 |
2,27 |
2,09 |
1,89 |
1,62 |
35 |
4,12 |
3,26 |
2,87 |
2,64 |
2,48 |
2,37 |
2,22 |
2,04 |
1,83 |
1,57 |
40 |
4,08 |
3,23 |
2,84 |
2,61 |
2,45 |
2,34 |
2,18 |
2,00 |
1,79 |
1,51 |
45 |
4,06 |
3,21 |
2,81 |
2,58 |
2,42 |
2,31 |
2,15 |
1,97 |
1,76 |
1,48 |
50 |
4,03 |
3,18 |
2,79 |
2,56 |
2,40 |
2,29 |
2,13 |
1,95 |
1,74 |
1,44 |
60 |
4,00 |
3,15 |
2,76 |
2,52 |
2,37 |
2,25 |
2,10 |
1,92 |
1,70 |
1,39 |
70 |
3,98 |
3,13 |
2,74 |
2,50 |
2,35 |
2,23 |
2,07 |
1,89 |
1,67 |
1,35 |
80 |
3,96 |
3,11 |
2,72 |
2,49 |
2,33 |
2,21 |
2,06 |
1,88 |
1,65 |
1,31 |
90 |
3,95 |
3,10 |
2,71 |
2,47 |
2,32 |
2,20 |
2,04 |
1,86 |
1,64 |
1,28 |
100 |
3,94 |
3,09 |
2,70 |
2,46 |
2,30 |
2,19 |
2,03 |
1,85 |
1,63 |
1,26 |
125 |
3,92 |
3,07 |
2,68 |
2,44 |
2,29 |
2,17 |
2,01 |
1,83 |
1,60 |
1,21 |
150 |
3,90 |
3,06 |
2,66 |
2,43 |
2,27 |
2,16 |
2,00 |
1,82 |
1,59 |
1,18 |
200 |
3,89 |
3,04 |
2,65 |
2,42 |
2,26 |
2,14 |
1,98 |
1,80 |
^,57 |
1,14 |
300 |
3,87 |
3,03 |
2,64 |
2,41 |
2,25 |
2,13 |
1,97 |
1,79 |
1,55 |
1,10 |
400 |
3,86 |
3,02 |
2,63 |
2,40 |
2,24 |
2,12 |
1,96 |
1,78 |
1,54 |
1,07 |
500 |
3,86 |
3,01 |
2,62 |
2,39 |
2,23 |
2,11 |
1,96 |
1,77 |
1,54 |
1,06 |
1000 |
3,85 |
3,00 |
2,61 |
2,38 |
2,22 |
2,10 |
1,95 |
1,76 |
1,53 |
1,03 |
oo |
3,84 |
2,99 |
2,60 |
2,37 |
2,21 |
2,09 |
1,94 |
1,75 |
1,52 |
1,00 |
Приложение 2
Критические значения t-критерия Стьюдента при уровне значимости 0,10, 0,05, 0,01 (двухсторонний)
Число степеней свободы |
a |
Число степеней свободы |
а |
||||
d.f.
|
0,10 |
0,05 |
0,01 |
d.f.
|
0,10 |
0,05 |
0,01 |
1 |
6,3138 |
12,706 |
63,657 |
18 |
1,7341 |
2,1009 |
2,8784 |
2 |
2,9200 |
4,3027 |
9,9248 |
19 |
1,7291 |
2,0930 |
2,8609 |
3 |
2,3534 |
3,1825 |
5,8409 |
20 |
1,7247 |
2,0860 |
2,8453 |
4 |
2,1318 |
2,7764 |
4,6041 |
21 |
1,7207 |
2,0796 |
2,8314 |
5 |
2,0150 |
2,5706 |
4,0321 |
22 |
1,7171 |
2,0739 |
2,8188 |
6 |
1,9432 |
2,4469 |
3,7074 |
23 |
1,7139 |
2,0687 |
2,8073 |
7 |
1,8946 |
2,3646 |
3,4995 |
24 |
1,7109 |
2,0639 |
2,7969 |
8 |
1,8595 |
2,3060 |
3,3554 |
25 |
1,7081 |
2,0595 |
2,7874 |
9 |
1,8331 |
2,2622 |
3,2498 |
26 |
1,7056 |
2,0555 |
2,7787 |
10 |
1,8125 |
2,2281 |
3,1693 |
27 |
1,7033 |
2,0518 |
2,7707 |
11 |
1,7959 |
2,2010 |
3,1058 |
28 |
1,7011 |
2,0484 |
2,7633 |
12 |
1,7823 |
2,1788 |
3,0545 |
29 |
1,6991 |
2,0452 |
2,7564 |
13 |
1,7709 |
2,1604 |
3,0123 |
30 |
1,6973 |
2,0423 |
2,7500 |
14 |
1,7613 |
2,1448 |
2,9768 |
40 |
1,6839 |
2,0211 |
2,7045 |
15 |
1,7530 |
2,1315 |
2,9467 |
60 |
1,6707 |
2,0003 |
2,6603 |
16 |
1,7459 |
2,1199 |
2,9208 |
120 |
1,6577 |
1,9799 |
2,6174 |
17 |
1,7396 |
2,1098 |
2,8982 |
∞ |
1,6449 |
1,9600 |
2,5758 |
Приложение 3
Значения статистик Дарбина-Уотсона при 5%-ном уровне значимости
n |
к1=1 |
kl=2 |
kl=3 |
kl=4 |
kl=5 |
||||||
|
dL |
du |
dL |
du |
dL |
dv |
dL |
du |
dL |
du |
|
6 |
0,61 |
1,40 |
- |
- |
- |
- |
|
|
|
|
|
7 |
0,70 |
1,36 |
0,47 |
1,90 |
- |
- |
|
|
|
|
|
8 |
0,76 |
1,33 |
0,56 |
1,78 |
0,37 |
2,29 |
|
|
|
|
|
9 |
0,82 |
1,32 |
0,63 |
1,70 |
0,46 |
2,13 |
|
|
|
|
|
10 |
0,88 |
1,32 |
0,70 |
1,64 |
0,53 |
2,02 |
|
|
|
|
|
11 |
0,93 |
1,32 |
0,66 |
1,60 |
0,60 |
1,93 |
|
|
|
|
|
12 |
0,97 |
1,33 |
0,81 |
1,58 |
0,66 |
1,86 |
|
|
|
|
|
13 |
1,01 |
1,34 |
0,86 |
1,56 |
0,72 |
1,82 |
|
|
|
|
|
14 |
1,05 |
1,35 |
0,91 |
1,55 |
0,77 |
1,78 |
|
|
|
|
|
16 |
1,10 |
1,37 |
0,98 |
1,54 |
0,86 |
1,73 |
0,74 |
1,93 |
0,62 |
2,15 |
|
17 |
1,13 |
1,38 |
1,02 |
1,54 |
0,90 |
1,71 |
0,78 |
1,90 |
0,67 |
2,10 |
|
18 |
1,16 |
1,39 |
1,05 |
1,53 |
0,93 |
1,69 |
0,82 |
1,87 |
0,71 |
2,06 |
|
19 |
1,18 |
1,40 |
1,08 |
1,53 |
0,97 |
1,68 |
0,86 |
1,85 |
0,75 |
2,02 |
|
20 |
1,20 |
1,41 |
1,10 |
1,54 |
1,00 |
1,68 |
0,90 |
1,83 |
0,79 |
1,99 |
|
21 |
1,22 |
1,42 |
1,13 |
1,54 |
1,03 |
1,67 |
0,93 |
1,81 |
0,83 |
1,96 |
|
22 |
1,24 |
1,43 |
1,15 |
1,54 |
1,05 |
1,66 |
0,96 |
1,80 |
0,86 |
1,94 |
|
23 |
1,26 |
1,44 |
1,17 |
1,54 |
1,08 |
1,66 |
0,99 |
1,79 |
0,90 |
1,92 |
|
24 |
1,27 |
1,45 |
1,19 |
1,55 |
1,10 |
1,66 |
1,01 |
1,78 |
0,93 |
1,90 |
|
25 |
1,29 |
1,45 |
1,21 |
1,55 |
1,12 |
1,66 |
1,04 |
1,77 |
0,95 |
1,89 |
|
26 |
1,30 |
1,46 |
1,22 |
1,55 |
1,14 |
1,65 |
1,06 |
1,76 |
0,98 |
1,88 |
|
27 |
1,32 |
1,47 |
1,24 |
1,56 |
1,16 |
1,65 |
1,08 |
1,76 |
1,01 |
1,86 |
|
28 |
1,33 |
1,48 |
1,26 |
1,56 |
1,18 |
1,65 |
1,10 |
1,75 |
1,03 |
1,85 |
|
29 |
1,34 |
1,48 |
1,27 |
1,56 |
1,20 |
1,65 |
1,12 |
1,74 |
1,05 |
1,84 |
|
30 |
1,35 |
1,49 |
1,28 |
1,57 |
1,21 |
1,65 |
1,14 |
1,74 |
1,07 |
1,83 |
|
Приложение 4
Варианты заданий для студентов заочного отделения
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
1 |
1 1 1 1 1 |
2 2 2 2 2 |
3 3 3 3 3 |
4 4 4 4 4 |
5 5 5 5 5 |
6 6 6 6 6 |
7 7 7 7 7 |
8 8 8 8 8 |
9 9 9 9 9 |
10 10 10 10 10 |
2 |
11 11 11 11 11 |
12 12 12 12 12 |
13 13 13 13 13 |
14 14 14 14 14 |
15 15 15 15 15 |
16 16 16 16 16 |
17 17 17 17 17 |
18 18 18 18 18 |
19 19 19 19 19 |
20 20 20 20 20 |
3 |
1 2 3 4 21 |
2 3 4 5 22 |
3 4 5 6 23 |
4 5 6 7 24 |
5 6 7 8 25 |
6 7 8 9 26 |
7 8 9 10 27 |
8 9 10 11 28 |
9 10 11 12 29 |
10 11 12 13 30 |
4 |
11 12 13 14 31 |
12 13 14 15 32 |
13 14 15 16 33 |
14 15 16 17 34 |
15 16 17 18 35 |
16 17 18 19 36 |
17 18 19 20 37 |
18 19 20 1 38 |
19 20 1 2 39 |
20 1 2 3 40 |
5 |
1 3 5 7 1 |
2 4 6 8 2 |
3 5 7 9 3 |
4 6 8 10 4 |
5 7 9 11 5 |
6 8 10 12 6 |
7 9 11 13 7 |
8 10 12 14 8 |
9 11 13 15 9 |
10 12 14 16 10 |
6 |
11 13 15 17 11 |
12 14 16 18 12 |
13 15 17 19 13 |
14 16 18 20 14 |
15 17 19 1 15 |
16 18 20 2 16 |
17 19 1 3 17 |
18 20 2 4 18 |
19 1 3 5 19 |
20 2 4 6 20 |
7 |
1 4 7 10 21 |
2 5 8 11 22 |
3 6 9 12 23 |
4 7 10 13 24 |
5 8 11 14 25 |
6 9 12 15 26 |
7 10 13 16 27 |
8 11 14 17 28 |
9 12 15 18 29 |
10 13 16 19 30 |
8 |
11 14 17 20 31 |
12 15 18 1 32 |
13 16 19 2 33 |
14 17 20 3 34 |
15 18 1 4 35 |
16 19 2 5 36 |
17 19 3 6 37 |
18 20 4 7 38 |
19 1 5 8 39
|
20 2 6 9 40 |
9 |
1 5 9 13 1 |
2 6 10 14 2 |
3 7 11 15 3 |
4 8 12 16 4 |
5 9 13 17 5 |
6 10 14 18 6 |
7 11 15 19 7 |
8 12 16 20 8 |
9 13 17 1 9 |
10 14 18 2 10 |
0 |
11 15 19 3 11 |
12 16 20 4 12 |
13 17 1 5 13 |
14 18 2 6 14 |
15 19 3 7 15 |
16 20 4 8 16 |
17 1 5 9 17 |
18 2 6 10 18 |
19 3 7 11 19 |
20 4 8 12 20 |
Вариант контрольной работы для студентов заочного отделения содержит 5 заданий: 4 задачи (по темам «Парная регрессия», «Множественная регрессия», «Системы одновременных уравнений», «Временные ряды») и 1 теоретический вопрос. Задания контрольной работы должны выбираться студентами по двум последним цифрам его учебного номера (номер студенческого билета) в соответствии с таблицей выбора вариантов. В первой колонке таблицы по вертикали расположены цифры от 1 до 0, и каждая из них – предпоследняя цифра личного номера. В первой строке таблицы по горизонтали также расположены цифры от 1 до 0, и каждая из них – последняя цифра личного номера Пересечения вертикальных (А) и горизонтальных (Б) линий определяют номера заданий контрольной работы, записанные столбиком. Например, если личный шифр студента имеет две последние цифры 75, то он должен выполнить номера 5 (тема 1), 8 (тема 2), 11 (тема 3), 14 (тема 4), 6 (вопрос).
Учебное издание
Алексей Фруминович Рогачёв
Ольга Александровна Заяц
Эконометрика
Учебное пособие
В авторской редакции
Компьютерная верстка О.А.Заяц
Подписано в печать 29.04.09 . Формат 60-84 1/16.
Гарнитура Times. Печать офсетная.Усл. печ. л. 5,0.
Тираж 100 экз. Заказ № ____.
Издательско-полиграфический комплекс ВГСХА «Нива».
400002, Волгоград, пр-т. Университетский, 26




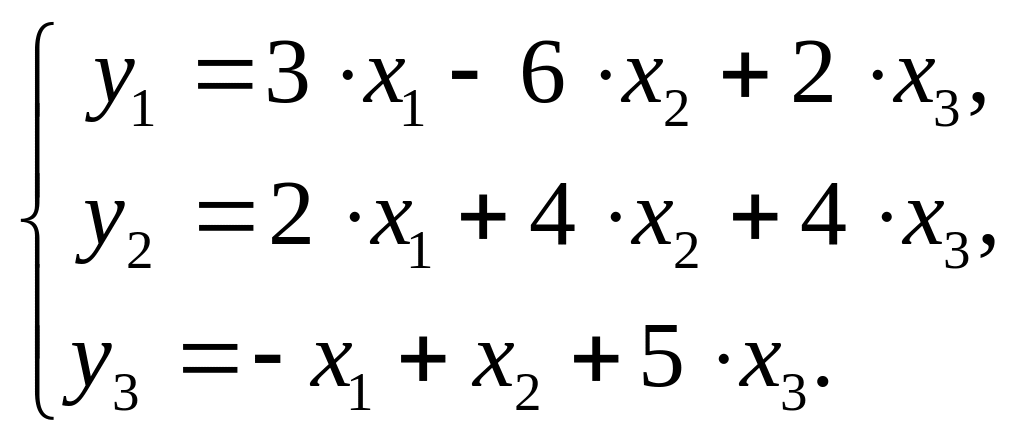



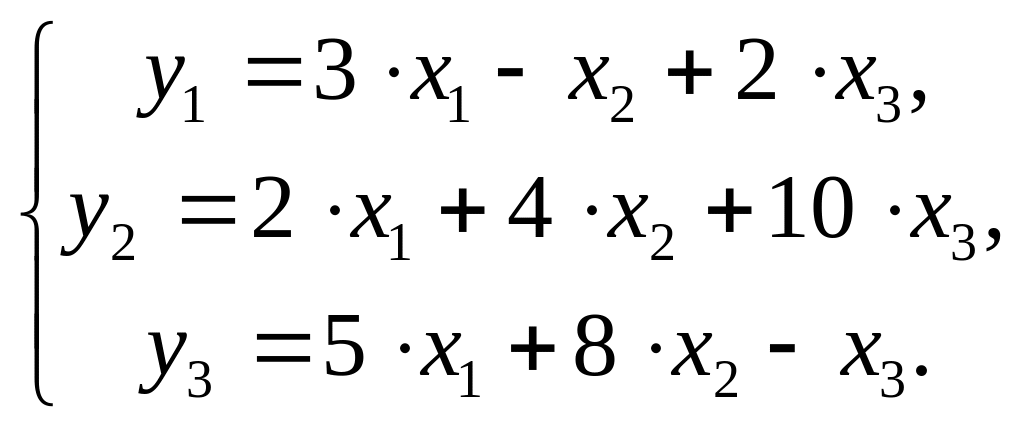












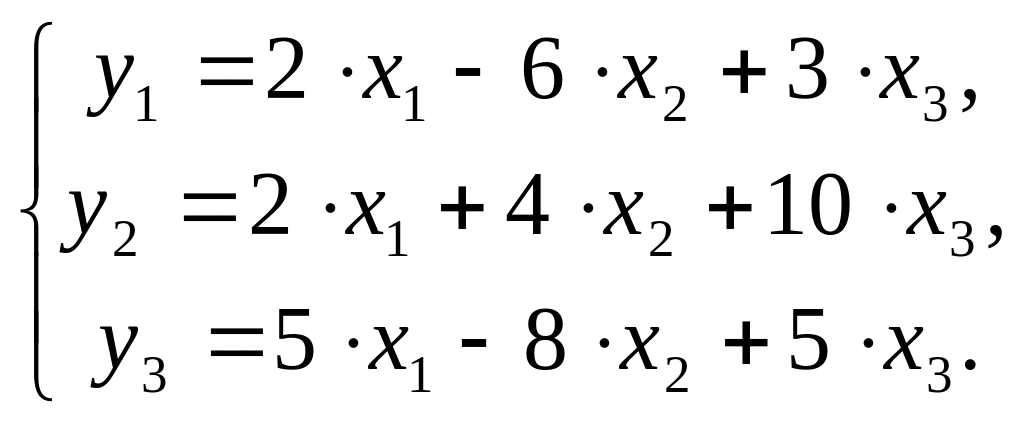


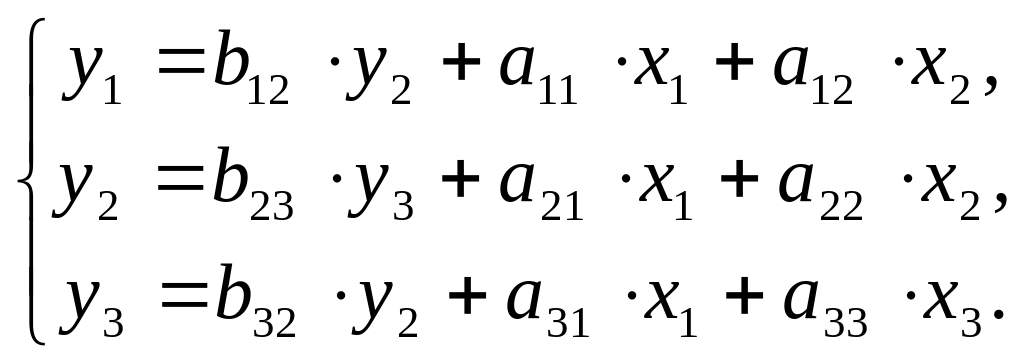




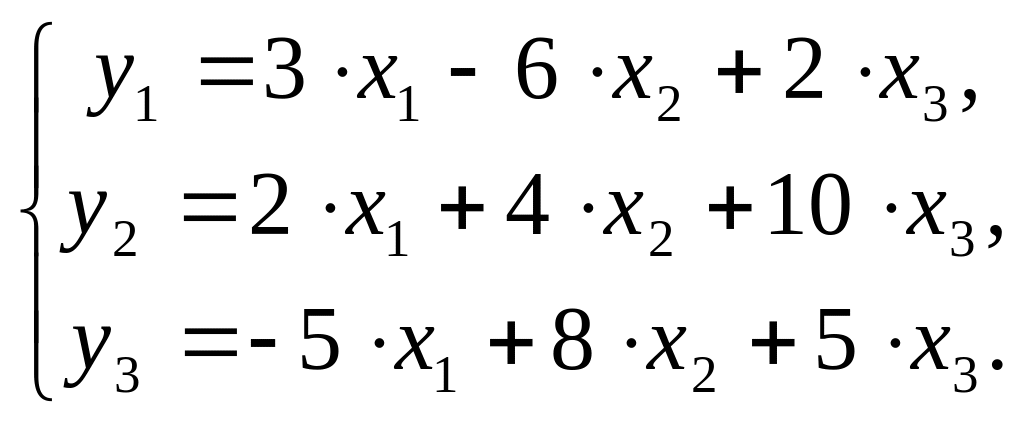






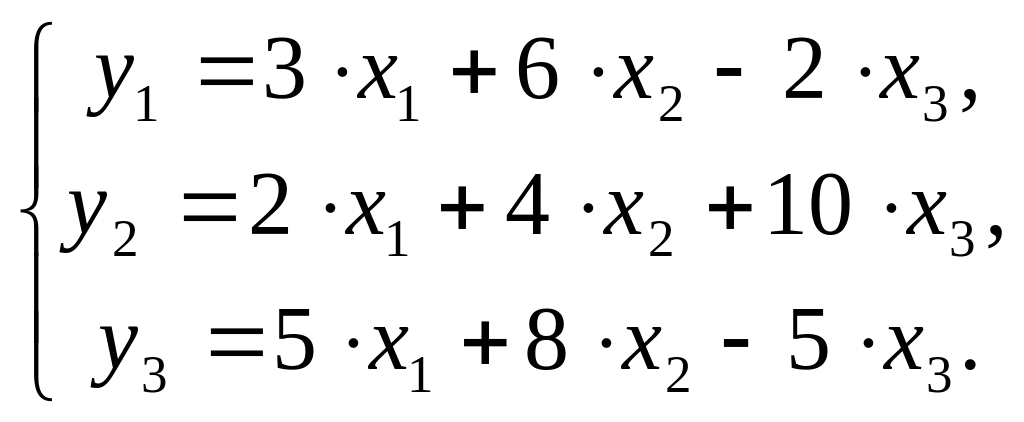
 k1
k1 k1
k1