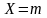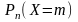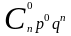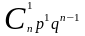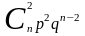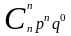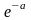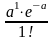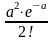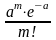- •Введение.
- •Часть 1. Элементы теории вероятностей.
- •§ 1. Случайная величина. Задание законов ее распределения.
- •§ 2. Числовые характеристики случайной величины.
- •§ 3. Законы распределения вероятностей дискретных случайных величин.
- •Равномерное распределение вероятностей дискретной случайной величины.
- •2. Биномиальное распределение вероятностей дискретной случайной величины.
- •3. Закон распределения Пуассона.
- •4. Гипергеометрическое распределение вероятностей дискретной случайной величины.
- •5. Геометрическое распределение вероятностей дискретной случайной величины.
- •§ 4. Законы распределения вероятностей непрерывных случайных величин.
- •1. Равномерное распределение вероятностей непрерывной случайной величины.
- •2. Экспоненциальное (показательное) распределение вероятностей непрерывной случайной величины.
- •3. Нормальное распределение вероятностей непрерывной случайной величины.
- •4. Распределения, связанные с нормальным распределением.
- •5. Распределение Вейбулла.
- •§ 5. Оценка отклонения теоретического распределения от нормального. Асимметрия и эксцесс.
- •Часть 2. Элементы математической статистики.
- •§ 1. Выборка и ее распределение.
- •§ 2. Статистические оценки.
- •1. Несмещенные, эффективные и
- •3. Другие характеристики вариационного ряда.
- •4. Эмпирические моменты.
- •5. Асимметрия и эксцесс эмпирического распределения.
- •6. Число степеней свободы.
- •7. Точечная и интервальная оценки.
- •8. Доверительный интервал для оценки математического ожидания нормального распределения при известном и в случае неизвестного .
- •9. Доверительный интервал для оценки среднего
- •§ 3. Проверка статистических гипотез.
- •§ 4. Проверка гипотезы о распределении генеральной совокупности. Критерий Пирсона. Критерий Колмогорова.
- •Часть 3. Примеры анализа экспериментальных данных.
- •§ 1. Общие положения.
- •§ 2. Составление вариационного ряда. Графическое представление результата. Нахождение среднего значения и дисперсии.
- •§ 3. Проверка гипотезы о распределении Вейбулла.
- •І. Применение критерия Пирсона.
- •Іі. Применение критерия Колмогорова.
- •§ 4. Проверка гипотезы о показательном распределении случайной величины.
- •І. Применение критерия Пирсона.
- •Іі. Применение критерия Колмогорова.
- •§ 5. Проверка гипотезы о нормальном распределении случайной величины.
- •І. Применение критерия Пирсона.
- •Іі. Применение критерия Колмогорова.
- •§ 6. Замечания.
- •§ 7. Применение вычислительной техники.
- •Задания и варианты данных для лабораторной работы.
- •Часть 4. Применение элементов математической статистики.
- •§ 1. Применение элементов математической статистики для оценки надежности машин.
- •§ 2. Применение элементов математической статистики при обосновании параметров зерноочистительной машины.
- •Заключение.
- •Приложение.
- •Значения коэффициентов вариации для различных законов распределения.
- •Критерий Колмогорова .
- •Значения коэффициентов распределения Вейбулла
- •Значения чисел в зависимости от
- •Отклонения
- •Литература.
- •§4. Законы распределения вероятностей непрерывных
§ 3. Законы распределения вероятностей дискретных случайных величин.
Равномерное распределение вероятностей дискретной случайной величины.
Дискретная
случайная величина, принимающая
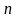 значений, распределена равномерно,
если вероятность того, что
примет
определенное значение
выражается формулой
значений, распределена равномерно,
если вероятность того, что
примет
определенное значение
выражается формулой
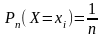 .
.
Например, равномерному закону распределения подчиняется случайная величина, означающая число появлений герба при одном подбрасывании монеты
2. Биномиальное распределение вероятностей дискретной случайной величины.
Биномиальным
распределением является
распределение вероятностей появления
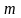 числа событий в
независимых испытаниях, в каждом из
которых вероятность появления события
постоянна и равна
числа событий в
независимых испытаниях, в каждом из
которых вероятность появления события
постоянна и равна
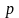 .
Вероятность возможного числа появления
события вычисляется по формуле Бернулли
.
Вероятность возможного числа появления
события вычисляется по формуле Бернулли
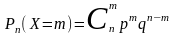 ,
,
где
 Постоянные
и
,
входящие в это выражение, являются
параметрами биномиального закона.
Постоянные
и
,
входящие в это выражение, являются
параметрами биномиального закона.
Биномиальное
распределение описывает распределение
вероятностей только дискретных случайных
величин. Возможными значениями случайной
величины
являются
 .
Биномиальному распределению подчиняется,
например, число бракованных изделий в
выборках из неограниченной партии
продукции.
.
Биномиальному распределению подчиняется,
например, число бракованных изделий в
выборках из неограниченной партии
продукции.
Биномиальное распределение может быть задано в виде таблицы:
|
0 |
1 |
2 |
… |
|
|
|
|
|
… |
|
Таблица 1
и в виде функции распределения
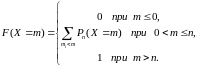
Если
случайная величина
имеет биномиальное распределение, то
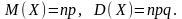
Особенностью
биномиальных распределений является
то, что вероятность
сначала возрастает при увеличении
и достигает наибольшего значения при
некотором наивероятнейшем значении
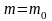 ,
которое можно определить из неравенства
,
которое можно определить из неравенства
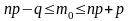 .
Значение
.
Значение
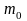 является модой биномиального закона.
Если имеются два наивероятнейших
значения, то распределение является
бимодальным. Отметим, что для любого
биномиального распределения расстояние
между математическим ожиданием и модой
не превосходит единицы. Если
является модой биномиального закона.
Если имеются два наивероятнейших
значения, то распределение является
бимодальным. Отметим, что для любого
биномиального распределения расстояние
между математическим ожиданием и модой
не превосходит единицы. Если
 -
целое число, то математическое ожидание
и мода совпадают. После достижения
наивероятнейшего значения
вероятность
начинает убывать. Распределение, вообще,
ассиметрично, за исключением случая,
когда
-
целое число, то математическое ожидание
и мода совпадают. После достижения
наивероятнейшего значения
вероятность
начинает убывать. Распределение, вообще,
ассиметрично, за исключением случая,
когда
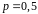 .
.
3. Закон распределения Пуассона.
Дискретная
случайная величина распределена по
закону Пуассона,
если вероятность того, что
примет
определенное значение
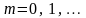 выражается формулой
выражается формулой
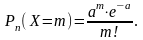
Закон
Пуассона описывает число событий
,
происходящих за одинаковые промежутки
времени при условии, что события
происходят независимо друг от друга с
постоянной средней интенсивностью. При
этом число испытаний
велико, а вероятность появления события
в каждом испытании
мала. Поэтому закон Пуассона называется
еще законом
распределения редких явлений.
Параметром распределения Пуассона
является величина
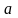 ,
характеризующая интенсивность появления
событий в
испытаниях (
,
характеризующая интенсивность появления
событий в
испытаниях (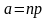 ).
).
Пуассоновским распределением хорошо описывается число требований на выплату страховых сумм за год, число вызовов, поступивших на телефонную станцию за определенное время суток.
Закон распределения Пуассона может быть задан в виде ряда:
|
0 |
1 |
2 |
… |
|
… |
|
|
|
|
… |
|
… |
Таблица 2
Если случайная
величина
имеет пуассоновское распределение, то