§ 2. Числовые характеристики случайной величины.

Закон распределения полностью характеризует случайную величину с вероятностной точки зрения. Но при решении ряда практических задач нет необходимости знать все возможные значения случайной величины и соответствующие им вероятности, а удобнее пользоваться некоторыми количественными показателями, которые давали бы в сжатой форме достаточную информацию о случайной величине. Такие показатели называются числовыми характеристиками случайной величины. Основными из них являются математическое ожидание, дисперсия, среднее квадратическое отклонение, мода и медиана.

Математическое ожидание характеризует положение случайной величины на числовой оси, определяя собой некоторое среднее значение, около которого сосредоточены все возможные значения случайной величины. Поэтому математическое ожидание иногда называют просто средним значением случайной величины.

Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на их вероятности:

Если дискретная случайная величина принимает бесконечное счетное множество значений, то ее математическое ожидание выражается формулой

Причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.

Математическим ожиданием непрерывной случайной величины , возможные значения которой принадлежат отрезку , называется определенный интеграл , т.е.

.

Если возможные значения случайной величины распределены по всей оси , то . Здесь предполагается, что несобственный интеграл, стоящий в правой части, сходится абсолютно, т.е. существует.

Свойства математического ожидания.

1. Математическое ожидание постоянной величины равно этой постоянной.

2. Постоянный множитель можно выносить за знак математического ожидания.

3. Математическое ожидание суммы конечного числа случайных величин равно сумме их математических ожиданий.

4. Математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий.

.

5. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю

.

К характеристикам положения случайной величины кроме математического ожидания относятся также мода и медиана.

Модой 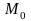дискретной случайной величины называется наиболее вероятное ее значение.

Модой непрерывной случайной величины называется такое ее значение, при котором плотность распределения имеет максимум. Геометрически моду можно интерпретировать как абсциссу точки максимума кривой распределения. Бывают двухмодальные и многомодальные распределения. Встречаются распределения, которые имеют минимум, но не имеют максимума. Такие распределения называются антимодальными.

Медианой случайной величины называется такое ее значение, для которой справедливо равенство

,

т.е. равновероятно, что случайная величина окажется меньше или больше медианы. С геометрической точки зрения медиана – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам. Так как вся площадь, ограниченная кривой распределения и осью абсцисс, равна единице, то функция распределения в точке, соответствующей медиане, равна 0,5: .

Следует отметить, что если распределение одномодально и симметрично, то математическое ожидание, мода и медиана совпадают.

С помощью таких характеристик как дисперсия и среднее квадратическое отклонение можно судить о рассеивании случайной величины вокруг математического ожидания.

Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания

.

Для дискретной случайной величины дисперсия равна сумме произведений квадратов отклонений значений случайной величины от ее математического ожидания на соответствующие вероятности

.

Для непрерывной случайной величины, закон распределения которой задан в виде плотности вероятности , дисперсия

.

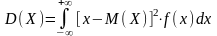Недостатком дисперсии является то, что она имеет размерность квадрата случайной величины и ее нельзя геометрически интерпретировать. Этого недостатка лишено среднее квадратическое отклонение случайной величины.

Средним квадратическим отклонением случайной величины называется арифметическое значение квадратного корня из ее дисперсии

.

Свойства дисперсии.

1. Дисперсия постоянной величины равна нулю

.

2. Постоянный множитель можно выносить за знак дисперсии, возводя его при этом в квадрат:

.

3. Дисперсия случайной величины равна разности матема-тического ожидания ее квадрата и квадрата математического ожидания самой величины:

.

4. Дисперсия суммы конечного числа независимых случайных величин равна сумме их дисперсий:

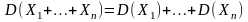
5. Дисперсия разности конечного числа независимых случайных величин равна сумме их дисперсий:

.

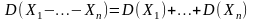Если бы величина Х имела несколько больших и маловероятных значений, то переход к величине Х², а тем более к величинам Х³, Х⁴ и т.д., позволил бы еще больше «усилить роль» этих больших, о маловероятных возможных значений. Вот почему оказывается целесообразным рассматривать математическое ожидание целой положительной степени случайной величины (как дискретной, так и непрерывной).

Начальным моментом порядка k случайной величины Х называется математическое ожидание величины X^k:

.

В частности, .

Пользуясь этими моментами, формулу для вычисления дисперсии можно записать так: .

Кроме моментов случайной величины Х целесообразно рассматривать моменты отклонения .

Центральным моментом порядка k случайной величины Х называется математическое ожидание величины :

.

В частности, ,

.

Нетрудно, исходя из определения центрального момента и пользуясь свойствами математического ожидания, получить формулы:

,

,

.

Моменты более высоких порядков применяются редко.

Замечание. Моменты рассмотренные здесь, называются теоретическими. В отличие от теоретических моментов, моменты, которые вычисляются по данным наблюдений, называются эмпирическими. Определения эмпирических моментов даны в части 2.