Кластерный анализ Содержание
Назначение кластерного анализа
|
|
Кластерный
анализ
– это совокупность методов, позволяющих
классифицировать многомерные наблюдения
( задача разбиения заданной выборки
объектов
(ситуаций) на подмножества, называемые
кластерами,
так, чтобы каждый кластер состоял
из схожих объектов, а объекты
разных кластеров существенно отличались).
Решение задачи кластеризации принципиально неоднозначно, и тому есть несколько причин:
не существует однозначно наилучшего критерия качества кластеризации. Известен целый ряд эвристических критериев, а также ряд алгоритмов, не имеющих чётко выраженного критерия, но осуществляющих достаточно разумную кластеризацию «по построению». Все они могут давать разные результаты.
число кластеров, как правило, неизвестно заранее и устанавливается в соответствии с некоторым субъективным критерием.
результат кластеризации существенно зависит от метрики, выбор которой, как правило, также субъективен и определяется экспертом.
Термин кластерный анализ, впервые введенный Трионом (Tryon) в 1939 году, включает в себя более 100 различных алгоритмов.
В отличие от задач классификации, кластерный анализ не требует априорных предположений о наборе данных, не накладывает ограничения на представление исследуемых объектов, позволяет анализировать показатели различных типов данных (интервальным данным, частотам, бинарным данным). При этом необходимо помнить, что переменные должны измеряться в сравнимых шкалах.
Кластерный анализ позволяет сокращать размерность данных, делать ее наглядной.
править задачи кластерного анализа
Задачи кластерного анализа можно объединить в следующие группы:
1. Разработка типологии или классификации.
2. Исследование полезных концептуальных схем группирования объектов.
3. Представление гипотез на основе исследования данных.
4. Проверка гипотез или исследований для определения, действительно ли типы (группы), выделенные тем или иным способом, присутствуют в имеющихся данных.
Как правило, при практическом использовании кластерного анализа одновременно решается несколько из указанных задач.
Цели кластеризации
Понимание данных путём выявления кластерной структуры. Разбиение выборки на группы схожих объектов позволяет упростить дальнейшую обработку данных и принятия решений, применяя к каждому кластеру свой метод анализа (стратегия «разделяй и властвуй»).
Сжатие данных. Если исходная выборка избыточно большая, то можно сократить её, оставив по одному наиболее типичному представителю от каждого кластера.
Обнаружение новизны (англ. novelty detection). Выделяются нетипичные объекты, которые не удаётся присоединить ни к одному из кластеров.
В первом случае число кластеров стараются сделать поменьше. Во втором случае важнее обеспечить высокую степень сходства объектов внутри каждого кластера, а кластеров может быть сколько угодно. В третьем случае наибольший интерес представляют отдельные объекты, не вписывающиеся ни в один из кластеров.
Во всех этих случаях может применяться иерархическая кластеризация, когда крупные кластеры дробятся на более мелкие, те в свою очередь дробятся ещё мельче, и т. д. Такие задачи называются задачами таксономии.
Результатом таксономии является древообразная иерархическая структура. При этом каждый объект характеризуется перечислением всех кластеров, которым он принадлежит, обычно от крупного к мелкому.
Классическим примером таксономии на основе сходства является биноминальная номенклатура живых существ, предложенная Карлом Линнеем в середине XVIII века. Аналогичные систематизации строятся во многих областях знания, чтобы упорядочить информацию о большом количестве объектов.
Независимо от предмета изучения применение кластерного анализа предполагает следующие этапы: — Отбор выборки для кластеризации. — Определение множества переменных, по которым будут оцениваться объекты в выборке. — Вычисление значений той или иной меры сходства между объектами. — Применение метода кластерного анализа для создания групп сходных объектов. — Проверка достоверности результатов кластерного решения.
Кластерный анализ предъявляет следующие требования к данным: во-первых, показатели не должны коррелировать между собой; во-вторых, показатели должны быть безразмерными; в-третьих, их распределение должно быть близко к нормальному; в-четвёртых, показатели должны отвечать требованию «устойчивости», под которой понимается отсутствие влияния на их значения случайных факторов; в-пятых, выборка должна быть однородна, не содержать «выбросов» (примечание 2). Если кластерному анализу предшествует факторный анализ, то выборка не нуждается в «ремонте» — изложенные требования выполняются автоматически самой процедурой факторного моделирования (есть ещё одно достоинство — z-стандартизация без негативных последствий для выборки; если её проводить непосредственно для кластерного анализа, она может повлечь за собой уменьшение чёткости разделения групп). В противном случае выборку нужно корректировать.
править Математические характеристики кластера
Кластер имеет следующие математические характеристики:
Центр кластера - это среднее геометрическое место точек в пространстве переменных.
Дисперсия кластера - это мера рассеяния точек в пространстве относительно центра кластера:
Среднеквадратичное отклонение (СКО) объектов относительно центра кластера:
Радиус кластера - максимальное расстояние точек от центра кластера:
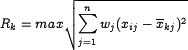
Спорный объект - это объект, который по мере сходства может быть отнесен к нескольким кластерам.
Размер кластера может быть определен либо по радиусу кластера, либо по среднеквадратичному отклонению объектов для этого кластера. Объект относится к кластеру, если расстояние от объекта до центра кластера меньше радиуса кластера. Если это условие выполняется для двух и более кластеров, объект является спорным.
Неоднозначность данной задачи может быть устранена экспертом или аналитиком.
Работа кластерного анализа опирается на два предположения: Первое предположение - рассматриваемые признаки объекта в принципе допускают желательное разбиение совокупности объектов на кластеры. Второе предположение - правильность выбора масштаба или единиц измерения признаков.