Лекция №13 Статистические методы для построения моделей вс.

Эти методы используются для представления свойств объекта в виде математических выражений, позволяющих выделить зависимость между программами и характеристиками, когда причинно-следственные отношения между ними трудно описать из-за их многообразия и действия случайных факторов.

При использовании статистических методов на основе эмпирических представлений о свойствах системы определяется состав признаков, характеризующих систему и тип статистической модели наиболее соответствующей этим знаниям. Таким образом создается множество характеристик Y, взаимосвязь между которыми должна быть определена с помощью статистических методов Y=F(x).

Путем измерения и регистрации, собираются статистические сведения о поведении системы, образующие статистическую выборку вида:

Методы регрессионного анализа.

При регулярном(???) анализе группная(???) связь задается в виде полинома y_i=f_i(x₁, x₂, …, x_n).

При применении анализа особое внимание следует уделять статистической независимости параметров, а также объему выборки, необходимого для получения достоверного результата.

При построении регрессивной модели наиболее важными являются следующие задачи:

1. выбор типа независимых аргументов;

2. выбор формы полинома, который представляет функциональную зависимость f(x_n);

Эта модель наиболее часто используется для анализа зависимостей воспроизводимых имитационных моделей.

040 Кондратьев А. (10.11, 17.11, 21.11)

Имитационные методы моделирования.

Широко используются при анализе ВС, они основаны на представлении порядка функционирования систем в виде алгоритма, который и называется имитационной моделью. При построении имитационных моделей используется агрегатный подход. Чтобы модель можно было построить, создаётся набор агрегатов элементов модели Ф₁,Ф₂, ... Ф_Q. Агрегаты соответствуют одному функциональному ресурсу. В качестве агрегатов могут выступать математические объекты, с помощью которых преобразуются соответствующие процессы.

А грегат – это описание функции некоторого объекта в аспектах, соответствующих цепи исследования. Функции агрегатов представляются в параметрической форме, т.е. в записи функции агрегатов используются параметры (производительность, быстродействие, ёмкость, длина слова, время выборки). Тогда функция агрегата Ф_g=Ф(a₁,a₂,…,a_n; b₁,b₂,…,b_l; c₁,c₂,…,c_m), где g={1..Q}. Параметры: a – описывают входные сигналы, b – определяют решение функционирования, с – определяют состояния выходов. Как бы не была сложна функция агрегата, она может быть представлена в виде чёрного ящика, у которого есть входы и выходы.

Если есть множество агрегатов, то мы имеем некоторые базисы имитационной модели, соединяя которые можно построить имитационную модель функционирования нашей системы.

Допустим, что базис имитационной модели состоит из определённых агрегатов: , , ,

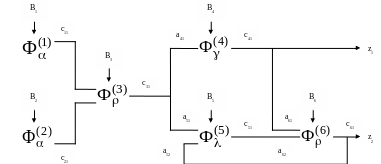
Путём обработки данных, наблюдаемых в характерных точках модели при реализации процедур, описанных агрегатами, можно получить оценки качества функционирования как отдельного агрегата, так и всей системы в целом.

Проведение имитационного моделирования можно разделить на следующие этапы:

1. определение принципов построения модели. Формируется общий замысел, состав характеристик и параметров, указывается область определения модели, формируются требования к точности, создаётся базис.

2. разработка самой модели. Создаётся программное моделирование, осуществляется проверка работоспособности модели и её адекватности.

3. моделирование на ЭВМ в интересующих нас режимах. Цель: получить информацию о поведении системы в условиях, задаваемых режимами функционирования. Выбрать наиболее оптимальный вариант функции.

Достоинство метода имитационного моделирования:

1. имеется возможность исследования системы любой степени сложности.

2. нет ограничения в степени детализации процесса.

3. метод гарантирует детальную оценку засчёт увеличения числа экспериментов.

Недостаток: сложность реализации, большие затраты времени моделирования, частный характер полученных результатов.