Задача идентификации и моделирования вс. Задача идентификации.

При эксплуатации ВС возникают задачи, связанные с идентификацией системы на базе введенных в нее новых элементов, структурных связей и подбора режима функционирования, соответствующего новым требованиям к качеству обслуживания пользователей. В этом случае необходимо заранее определить эффект, который возможно получить путем моделирования системы. Для этой цели проводятся измерения на реально функционирующей системе, строится модель системы на основе сведений о ее организации и проводится идентификация модели в реально существующей системе.

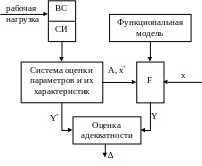
СИ – средства измерения

F – оператор

Процесс идентификации:

1). В соответствии с целью предлагается функциональная модель, которая является некоторой математической системой, позволяющей описать функционирование ВС. Этот этап носит название функциональная идентификация ВС.

2). В соответствии с данными, которые получены в процессе эксплуатации реальной ВС на реальной рабочей нагрузке, рассчитываются параметры x и характеристики X^*, Y^* и определяется множество параметров A, которые будут являться параметрами, реализующими функциональную модель. Реализация функциональной модели обозначена F. На основе множества параметров модели A могут быть определены параметры X и Y и характеристики Y реализации функциональной модели. Этот этап – параметрическая идентификация. Полученные характеристики Y могут быть сравнены с полученными и оценки их соответствия могут быть выражены в ∆ - погрешность идентификации. Если ∆ соответствует практическим требованиям, то модель является адекватной и может быть использована для исследования поведения ее в новых условиях. Процесс ее функционирования может быть описан как процесс определения новых характеристик от новых параметров: Y_н=F(x_н).

Лекция №12 Принципы построения и свойства моделей.

Модель – это физическая или абстрактная система, адекватно представляющая объект исследования. Абстрактная модель – описание объекта на некотором формальном языке. Абстрактные модели – ее компоненты не физические модели, а понятия, в качестве которых наиболее часто используются математические отношения. Абстрактная модель, основанная на математическом отношении, называется математической моделью. Математическая модель имеет форму функциональной зависимости:

Y=F(x).

Y – набор характеристик Y={y₁, y₂, …, y_m}

X – набор параметров X={x₁, x₂, …,x_n}

F – функция воспроизводящая модель.

Модель создается исходя из цели исследования, которая определяет

1). состав характеристик Y,

2 ). состав параметров X,

3). область определения модели

4). задается точность, как предельная допустимая погрешность оценки Y на модели. Модель, построенная на основе этих принципов, называется адекватной системе моделью. Свойства адекватности модели являются относительными. Они связаны с целью исследования. Больше всего адекватность определяется в точности воспроизведения. Если не найдена точность, то модель не может считаться адекватной. Высокая точность может быть получена только в узкой окрестности точки x. Чем больше окрестность точки x, тем более сложной должна быть модель.

Кроме адекватности, к свойствам модели относятся:

1). мощность,

2). размерность,

3). сложность вычислений.

Размерность – число величин, представленных в модели, параметры и характеристики(X и Y).

Сложность вычислений – оценивается числом операций, приходящихся на одну реализацию оператора F. Напрямую связана с затратами вычислительного времени.

Т.к. процессы, протекающие в ВС, носят характер случайных, то в качестве математической базы используемой как метод исследования ВС наиболее часто используют аппарат теории вероятностей и математической статистике. При этом случайные величины, соответствующие параметрам, характеристикам и другими элементами моделей могут быть представлены на разных уровнях, среди которых наиболее часто используются следующие:

1). Статистическая выборка,

2). Закон распределения случайной величины,

3). Математическое ожидание и дисперсия,

4). Математическое ожидание.