2.3. Кольца Ньютона
Интерференционная картина может быть получена в результате наложения когерентных волн при отражении света от поверхностей кольцевого зазора толщиной d (рисунок 14), образованного плоскопараллельной пластиной и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны R.
Центр
кривизны линзы находится в точке С
на рисунке 14.
При
нормальном падении на линзу световой
волны длиной λ, один из лучей которой
обозначен цифрой 1 на рисунке 14, в
отраженном свете наблюдаются
концентрические кольца, при этом в
центре интерференционной картины
располагается темное пятно.
Усиление
или ослабление света (то есть светлое
или темное кольцо) будет наблюдаться
в том случае, если на оптической разности
хода лучей, отраженных от верхней и
нижней границ кольцевого зазора
(например, в точках А
и В
на рисунке 14) будет укладываться
соответственно четное или нечетное
число полуволн.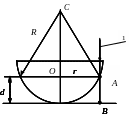
А
r
Рисунок 14
Радиусы светлых колец Ньютона в отраженном свете:
,
где n - показатель преломления среды в кольцевом зазоре между линзой и пластиной, а величина m=1,2,3,….
Радиусы темных колец Ньютона в отраженном свете:
,
где m=0,1,2,3, ….
Отметим, что если свет будет проходящим, то там, где в отраженном свете наблюдалось светлое кольцо, в проходящем свете будет располагаться темное и, наоборот, там, где было темное кольцо в отраженном свете, в проходящем будет наблюдаться светлое кольцо.
Укажем также, что если свет является белым, то наблюдаются цветные кольца Ньютона.
2.4. Дифракция света. Дифракционная решетка
Под дифракцией понимается любое отклонение волн от прямолинейного направления при их распространении в среде с резкими неоднородностями, в качестве которых могут выступать, например, края экранов и отверстий. Для света это связано с отклонениями от законов геометрической оптики, что приводит к огибанию световыми волнами препятствий и к проникновению света в область геометрической тени.
Д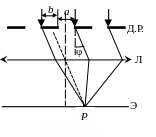
ифракция
отчетливо наблюдается только в том
случае, если характерный размер
препятствия, которое огибает волна,
например, диаметр диска, будет соизмерим
с длиной волны.
Здесь мы будем рассматривать
дифракцию только на прозрачных
д
Рисунок 15
Суммарная ширина прозрачного а и непрозрачного b промежутков образует период d дифракционной решетки:
d=а+b.
В соответствии с принципом Гюйгенса-Френеля, каждая точка любой щели дифракционной решетки является источником когерентных волн, интерференция которых будет давать дифракционную картину на экране Э, установленном в фокальной плоскости собирающей линзы Л (рисунок 15) за дифракционной решеткой (Д.Р.).
При наблюдении дифракции в монохроматическом свете (то есть для световых волн, имеющих строго определенную длину или частоту), в центре экрана будет наблюдаться светлая (С) полоса (максимум интенсивности света), относительно которой будут симметрично располагаться темные (Т) полосы (минимумы интенсивности света) и светлые (С) полосы (максимумы интенсивности света), рисунок 16.
При
наблюдении дифракции в белом
свете
относительно центрального светлого
(С)
дифракционного
максимума
будут
симметрично
располагаться
цветные
полосы, разделенные темными промежутками
(рисунок 17), при этом фиолетовые
полосы
(Ф) обращены к центру, а красные (К) - к
краям дифракционной картины, так как
длина волны красного света больше, чем
фиолетового.
-
Т
С
Т
С
Т
С
Т
Рисунок 16
-
Т
К-Ф
Т
С
Т
Ф-К
Т
Рисунок 17
Наиболее отчетливо наблюдаются главные максимумы и минимумы интенсивности света, возникающие на экране при интерференции световых когерентных волн, идущих от всех щелей дифракционной решетки.
Вспомогательные максимумы и минимумы интенсивности возникают в результате интерференции световых волн, идущих от соседних щелей решетки. Интенсивность вспомогательных максимумов мала, по сравнению с главными, и здесь мы их рассматривать не будем.
Условия главных максимумов интенсивности при наблюдении дифракции в монохроматическом свете:
,
,
а главных минимумов:
,
,
где m - порядок максимума (или, соответственно, минимума) интенсивности; - угол дифракции.
При наблюдении дифракции в белом свете условия главных максимумов и минимумов имеют тот же вид, при этом, в случае максимумов величина m называется порядком спектра.
Разрешающая способность дифракционной решетки:
R=λ /Δλ=mN
Здесь Δλ- наименьшая разность длин волн двух соседних спектральных линий, при которой эти линии могут быть видны раздельно с помощью дифракционной решетки; N- число штрихов решетки.
Угловая дисперсия дифракционной решетки:
Линейная дисперсия дифракционной решетки:
,
где F - фокусное расстояние линзы, в фокальной плоскости которой наблюдается дифракционная картина.