Заключение

Основной целью при изучении методов и средств теории принятия решений является выявление их системно-комплексного единства. В области линейного программирования наиболее явно данное свойство проявляется в изоморфизме отдельных моделей в процессе применения методологии «спора моделей». Каждая из указанных моделей возникает в результате рассмотрения объекта исследования на соответствующем уровне абстрактного описания рационально-эмпирического комплекса систем.

Применение рационально-эмпирического подхода и задачного принципа на практике создают условия для формирования системообразующих основ в системном анализе и исследовании операций. «Только при полном понимании задач можно найти соответствующие способы их решения. Для результатов важнее поставить правильные вопросы, чем правильно ответить на ошибочные» [5, с.19].

Необходимо отдавать себе отчет в том, что рассмотренные задачи линейного программирования представляют собой частные случаи более широких классов задач, имеющих важное научно-практическое значение и решаемых в инженерной деятельности.

Библиографический список

1. Shannon R.E., Biles W.E. The Utility of Certain Curriculum Topics to Operation Research Practitioners, Operation Research, v. 18, №4, Jul. Aug. 1970.

2. Weston F.C. OR Technologues Relevant to Corporate Peanning Function Practices, An Investigative Look, presented at 39^th National Meeting, Operation Practices Society of America, Operation Research Bulletin, v.19, Suppl.2, Spring, 1971.

3. Исследование операций в экономике. Учебн. пособие для вузов. Н.Ш. Кремер, Б.А. Путка, И.М. Тришин, М.Н. Фридман/ Под ред. проф. Н.М. Кремера – М.: Банки и биржи, ЮНИТИ, 1999. – 408 с.

4. Панченко В. М. Теория систем: Учебное пособие. М: –МИРЭА (ТУ), 1996 – 128 с.

5. Клир Дж. Системология. Автоматизация решений системных задач. – М.: Радио и связь, 1990. – 540с.

6. Вентцель Е.С. Исследование операций: задачи, принципы, методология. – М.: Советское радио, 1972.

7. Грешилов А.А. Как принять наилучшее решение в реальных условиях. – М: Радио и связь, 1991. – 320 с.: ил.

8. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: Учеб. пособия для студентов втузов. В 2-х ч. Ч. 1. – 4-е изд., испр. и доп. – М.: Высш. шк.,1986. – 304 с.

9. Муртаф Б. Современное линейное программирование/ Пер. с англ. – М.: Мир, 1984. – 224 с.

10. Панченко В.М. Системный анализ. Метод имитационного моделирования: Учеб. пособие. – М.: МИРЭА, 1995. – 120 с.

11. Панченко В.М., Панов А.В. Системный анализ и исследование операций. Линейное программирование: Лабораторный практикум. – М.: МИРЭА, 2000. – 46 с.

12. Моисеев Н.Н. Математические задачи системного анализа. – М.: Наука. Главная редакция физико-математической литературы, 1981. – 488 с.

13. Волкова В.Н., Воронков В.А. и др. Теория систем и методы системного анализа в управлении и связи. – М.: Радио и связь, 1983. – 248 с.

14. Нечаев В.В., Панченко В.М. и др. Исследование операций и теория систем. Основы статистической динамики знаний: Учебное пособие. – М.: МИРЭА, 2000. – 83 с.

15. Рыков А.С. Методы системного анализа: оптимизация. – М.: НПО Экономика, 1999. – 255 с.

16. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. - М.: Наука, 1986. –544 с.

17. Таха Хэдми А. Введение в исследование операций, 6-е издание/ Пер. с англ. – М.: Вильямс, 2001. – 912 с.

18. Панов А.В. Теория систем. Модели и методы в инженерных исследованиях // Курс лекций. Часть I. – М.: Академия ФСБ РФ, 2001. – 95 с.

19. Панов А.В. Теория систем // Курс лекций. Часть II. – М.: Академия ФСБ РФ, 2001. – 64 с.

ПРИЛОЖЕНИЯ

Приложение 1

Проведение исследования

с помощью программы SIMPLEX1

Программа simplex1 написана на языке программирования Borland С++ v.3.1.

Исполняемый файл программы: simplex1.exe.

Минимальные системные требования:

0. IBM–совместимый персональный компьютер с процессором от 386 и выше;

1. оперативная память от 2 Mb;

2. 16 Kb на жестком диске;

3. операционная система MS–DOS 6.xx.

Приложение 2

Работа с программой

Ввод исходных данных

1. Ввести число уравнений и число переменных (без базисных).

Пример. Найти наименьшее значение линейной функции F=–X₁+7X₂+168 при следующих ограничениях:

X₁  0

X₂  0

X₃ = – X₁ – X₂ + 12  0

X ₄ = – X₁ + 10  0

X₅ = – X₂ + 12  0

X₆ = X₁ + X₂ – 1  0

Число уравнений: 4. Число свободных переменных: 2.

1. Заполнить симплекс-таблицу. Пример заполнения таблицы для данного примера показан на рис. П.2.1.

2. Ввести критерий поиска – минимум или максимум. В данной программе в целях упрощения алгоритма решения ОЗЛП поиск минимума целевой функции F сведен к поиску максимума функции – F. Поэтому в случае минимизации знаки коэффициентов целевой функции заменяются на противоположные.

Программа предоставляет возможность корректировки введенных данных. Если при вводе данных Вы не допустили ошибок, то после соответствующего запроса нажмите клавишу ‘Д’ (’д’, ’L’, ’l’) и продолжить работу, в противном случае следует нажать любую другую клавишу и повторить процедуру ввода.

Поиск решения

По ходу решения задачи программа будет задавать Вам вопросы, помогая проверять усвоение учебного материала. В случае неправильного ответа программа предъявит правильный и даст необходимые пояснения.

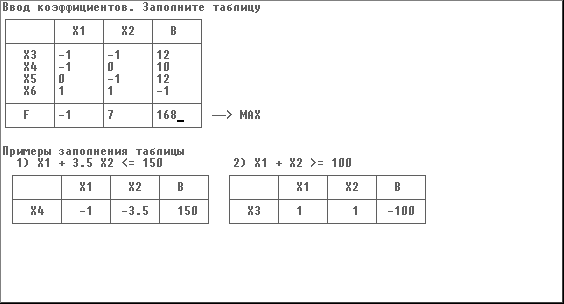
Рис. П.2.1. Заполнение симплекс-таблицы

Если текущий план является опорным, то начинается поиск оптимального решения, в противном случае необходимо найти опорный план.

Получив опорное решение, программа начинает оптимизацию целевой функции F.

Если план оптимален, то программа выводит на экран оптимальное значение функции и соответствующее ему решение (значения переменных) (см. рис. 2.4). После вывода результатов программа ожидает нажатия клавиши Enter для выхода в операционную систему.

Рис. П.2.2. Результат работы программы

Меняя значение коэффициентов в уравнениях ограничений и в целевой функции, проследить изменение оптимальных значений функции. Изменение одного из коэффициентов рассматривается как проведение однофакторного эксперимента, двух – как двухфакторного и т.д.

СОДЕРЖАНИЕ

Введение…………………………………………………………	3
1. Основные свойства и модели линейного программирования………………………………………………………………..	6
1.1. Граф-схема решения задачи линейного программирования………………………………………………………………..	6
1.2. Алгебраическая модель решения задачи линейного программирования…………………………………………………..	8
1.3. Геометрическая форма представления процесса решения.……………………………………………………………….	9
1.4. Свойства задач линейного программирования………………………………………………………………..	10
2. Симплекс-метод решения задачи линейного программирования……………………………………………………………...	13
2.1. Иллюстрация процесса поиска решения………………….	13
2.2. Алгебраическое решение…………………………………..	16
2.3. Табличный вариант замены переменных…………………	18
2.4. Система «Тренажер»……………………………………….	21
2.5. Система правил замены переменных……………………..	22
3. Инвестиционные проекты в концепции транспортной задачи ЛП…………………………………………………………..	24
3.1. Транспортная топология инвестиций. Формирование заданий……………………………………………………………..	24
3.2. Формирование конкретной системы данных задачи линейного программирования…………………………………….	27
3.3. Программа Random (Windows-версия)……………………	30
3.4. Экономическое содержание двойственности……………..	31
4. Транспортная задача линейного программирования……….	35
4.1. Составление опорного плана ТЗ по методу северо-западного угла (СЗУ)……………………………………………	35
4.2. Составление опорного плана ТЗ по методу минимума стоимостей перевозки…………………………………………..	36
4.3. Сравнение планов по критерию стоимости………………	40
4.4. Проверка лучшего опорного плана на оптимальность…..	40
4.5. Улучшение плана по методу циклических перестановок..	42
Заключение………………………………………………………	44
Библиографический список…………………………………….	45
Приложения……………………………………………………...	47
Приложение1…………………………………………………….	47
Приложение2…………………………………………………….	47

Виктор Михайлович Панченко

Александр Владимирович Панов

Теория принятия решений

линейное программирование

Учебное пособие

Редактор В.Б. Закорюкин

Литературный редактор Л.В. Омельянович

Изд. лицензия № 020456 от 04.03.97

Подписано в печать 14.01.2002. Формат 60x84 1/16.

Бумага офсетная. Печать офсетная. Усл. печ. л. 3,02.

Усл. кр.-отт. 12,08. Усл.-изд. л. 3,25. Тираж 100 экз. С 30

Московский государственный институт радиотехники,

электроники и автоматики (технический университет)