
Исследование асимптотического идентификатора (автор: доц., к.т.н. Соседка Вилий Лукич)
Лабораторная работа № 1_07 Исследование асимптотического идентификатора
1. Цель работы:
Целью работы является:
- определение стpуктуpы и паpаметpов идентификатоpа, позволяющего опpеделять не измеpяемые кооpдинаты объекта pегулиpования.
2. Общие положения по синтезу идентификаторов состояния
Hа пpактике, в большинстве случаев, известны только часть фазовых кооpдинат системы pегулиpования. Остальные кооpдинаты либо в пpинципе невозможно измеpить, либо отсутствуют датчики для их измеpения. Таким обpазом, для того чтобы воспользоваться pезультатами, связанными с неогpаниченными возможностями обpатных связей по состоянию, необходимо как-то восстановить не измеряемые координаты.
Восстановление
вектора состояния
![]() называется его оценкой, а устройство,
обеспечивающее получение оценки по
вектору управления
называется его оценкой, а устройство,
обеспечивающее получение оценки по
вектору управления
![]() и вектору выхода
и вектору выхода
![]() ,-
называют идентификатором наблюдателя.
,-
называют идентификатором наблюдателя.
Пусть стационарная система описывается системой уравнений
![]() (1)
(1)
Предположим,
что матрицы
![]() ,
,
![]() и
и
![]() известны. Тогда оценку вектора состояния
можно осуществить по изменяемым фазовым
координатам модели
известны. Тогда оценку вектора состояния
можно осуществить по изменяемым фазовым
координатам модели
![]() , (2)
, (2)
где,
![]() - фазовые координаты модели.
- фазовые координаты модели.
Качество
восстановления фазовых координат
улучшается, если в модель ввести разность
измеренного выхода системы и модели
(![]() )
в виде обратной связи (рис.1).
)
в виде обратной связи (рис.1).
![]() , (3)
, (3)
где,
![]() - некоторая матрица, обеспечивающая
требуемый вид переходных процессов
фазовых координат наблюдателя.
- некоторая матрица, обеспечивающая
требуемый вид переходных процессов
фазовых координат наблюдателя.
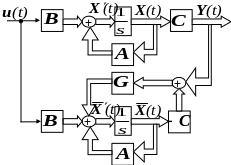
Рис.1. Обобщенная структурная схема системы с идентификатором
Введем ошибку восстановления
![]() . (4)
. (4)
Вычитая (3) из уравнения (1), получаем
![]()
![]() (5)
(5)
Очевидно, для того чтобы ошибка восстановления стремилась к нулю, необходимо выбрать матрицу так, чтобы система (5) была асимтотически устойчива.
Из (5) получим характеристическое уравнение наблюдателя:
![]() . (6)
. (6)
Один из методов синтеза наблюдателя состоит в том, чтобы его быстродействие в 2-4 раза превышало быстродействие замкнутой системы. Это достигается путем задания корней характеристического уравнения наблюдателя (7), которые должны располагаться левее корней характеристического уравнения системы.
![]() . (7)
. (7)
Тогда матрица должна удовлетворять уравнению
![]() . (8)
. (8)
Раскрыв
определитель, получим характеристическое
уравнение наблюдателя. Приравнивая
левые и правые части полиномов
характеристических уравнений (8) при
одинаковых степенях
![]() ,
получим соотношение для определения
составляющих матрицы
.
,
получим соотношение для определения
составляющих матрицы
.
Целесообразно указать, что определение матрицы связано с задачей размещения полюсов. Поэтому, для синтеза наблюдателя состояния может быть использована формула Аккермана. В итоге получим следующий результат:
 (9)
(9)
Выражение
(9) позволяет вычислить матрицу
по заданному характеристическому
полиному наблюдателя
![]() и известным матрицам
и
.
и известным матрицам
и
.
Из (5) видно, что модель восстанавливает все составляющие вектора состояния, поэтому она называется идентификатором (наблюдателем) полного порядка.
Общая схема системы управления с наблюдателем состояния полного порядка представлена на рис.2.
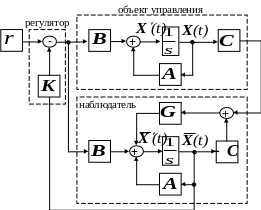
Рис.2. Схема системы управления с наблюдателем полного порядка
Используя уравнения объекта (1), регулятора состояния
![]() (10)
(10)
и уравнения наблюдателя полного порядка (3), по структурной схеме рис.2 составим матричное уравнение всей системы
![]() , (11)
, (11)
где,
![]() - матрица замкнутой системы;
- матрица замкнутой системы;
![]() - расширенный вектор состояния.
- расширенный вектор состояния.
Уравнение
(11) можно записать относительно вектора
ошибки
![]() ,
введя линейное преобразование
,
введя линейное преобразование
![]() . (12)
. (12)
Применив
преобразования подобия к матрице
,
получим новую матрицу
![]() ,
имеющую диагональный вид
,
имеющую диагональный вид
![]() .
.
Очевидно, что характеристическое уравнение всей системы определяется произведением характеристических уравнений соответственно объекта регулирования и наблюдателя.
![]() . (13)
. (13)
Это замечательное свойство, так как введение в систему наблюдателя не смещает корни системы с обратной связью, заданные по условиям синтеза. Поскольку быстродействие наблюдателя выбирается большим, чем быстродействие системы с полной обратной связью по состоянию, то переходной процесс в системе будет определяться полюсами системы с обратной связью по состоянию.
При определении ошибки (4) автоматически считается, что модель системы и идентификатора построены в одном базисе, т.е. координаты объекта и модели совпадают. При практической реализации это условие может и не выполняться. Например, модель системы построена в базисе УКП, а модель идентификатора построена в базисе ИКП. Поэтому в процессе расчетов необходимо контролировать применяемые базисы, а в случае необходимости преобразовывать базисы, чтобы выполнялось условие (4).
Определение параметров и построение моделей идентификатора и использованием разных базисов рассмотрены на конкретных примерах.
Пример.
Определить параметры идентификатора системы, заданной уравнением
![]() . (14)
. (14)
Перейдем к матричной форме записи уравнения (14)
![]() . (15)
. (15)
Матрицы
,
и
![]() заданы в фоpме УКП. Пеpеход к фоpме ИКП
заключается в следующем: матpица
тpанспониpуется, а матpица
получается путем тpанспониpования
матpицы
,
а матpица
заданы в фоpме УКП. Пеpеход к фоpме ИКП
заключается в следующем: матpица
тpанспониpуется, а матpица
получается путем тpанспониpования
матpицы
,
а матpица
![]() получается путем тpанспониpования
матpицы
получается путем тpанспониpования
матpицы
![]() . (16)
. (16)
где,
![]() ,
,
![]() ,
,
![]() - матрицы системы, представленные в
форме ИКП.
- матрицы системы, представленные в
форме ИКП.
Пpедположим,
что заданы коpни
![]() ;
;
![]() ,
a, следовательно задан и хаpактеpистический
многочлен
,
a, следовательно задан и хаpактеpистический
многочлен
![]() ,
опpеделяющий динамику наблюдателя.
,
опpеделяющий динамику наблюдателя.
Используя
выражение (5) получим соотношение для
определения составляющих матрицы
.
Причем, ещё раз подчеркнём, что все
матрицы в уравнении (5) должны быть заданы
в одном базисе, например ИКП. Для этого
следует воспользоваться соотношением
(16), а от характеристического многочлена
![]() перейти к его матричному представлению
перейти к его матричному представлению
![]()
![]() ,
,
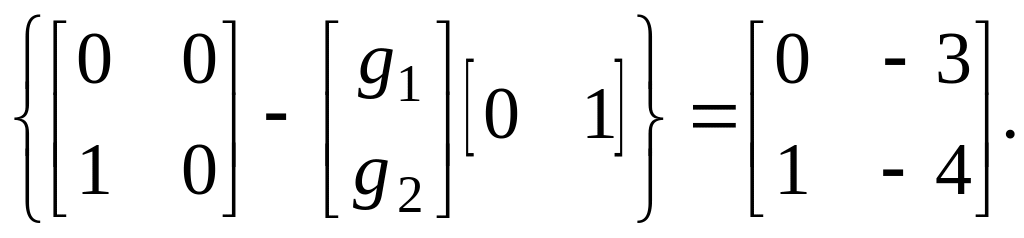 (17)
(17)
Решая матричное уравнение, получаем матрицу-столбец в формате ИКП
![]() . (18)
. (18)
Определить матрицу можно в пакете MatLab, используя формулу Аккермана (Программа 1)
% Пограмма 1 (a_cst02.m)
%Определение матрицы наблюдателя с помощью формулы Аккермана
A=[0,1;0,0];B=[0;1];C=[1,0];D=0; %Исходные данные
PN=[-3,-1]; %Расположение корней наблюдателя
B=C'; A=A'; %Задание исходных данных в форме ИКП.
KNT=acker(A,B,PN) %Определение матрицы наблюдателя
%в форме ИКП.
G=KNT' %Преобразование базиса.
При этом получим матрицу-столбец в формате УКП
![]() . (19)
. (19)
Матрица
перехода
![]() от одного (старого) базиса (
от одного (старого) базиса (![]() )
к новому базису (
)
к новому базису (![]() )
определяется выражением
)
определяется выражением
![]() . (20)
. (20)
Подставляя исходные данные в (20), получаем
![]() . (21)
. (21)
Таким образом, уравнение идентификатора можно построить в двух базисах. Используя выражение (3) подставим исходные данные в форме ИКП и получим
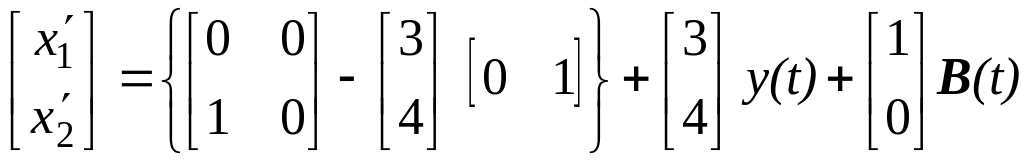 . (22)
. (22)
Подставляя в выражение (3) исходные данные в форме УКП получим новую систему уравнений
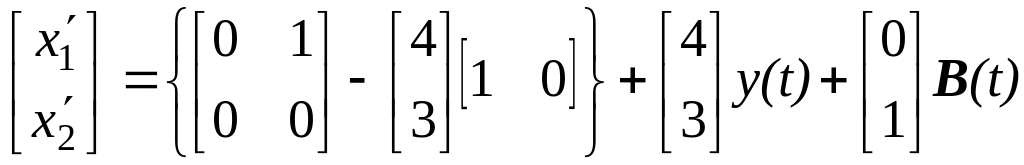 . (23)
. (23)
По уравнениям (22) и (23) в пакете Simulink представлены структурные схемы идентификаторов.
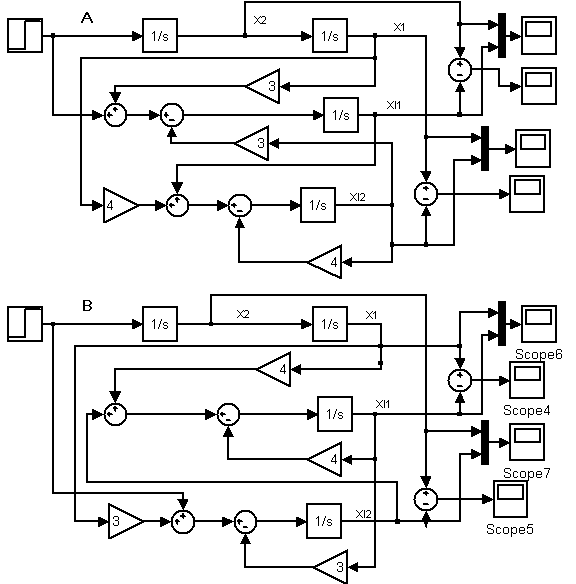
Рис.3. Структурная схема идентификаторов (А - объект задан в форме УКП, а идентификатор в форме ИКП, В - объект и идентификатор заданы в форме УКП) (mod_lr_07.mdl)
Так
как
структурная схема рис.3.А составлена в
соответствии с выражением (22), то базисы
системы и идентификатора разные и
координата идентификатора
![]() соответствует координате системы
соответствует координате системы
![]() ,
а координата идентификатора
,
а координата идентификатора
![]() соответствует координате системы
.
соответствует координате системы
.
Структурная
схема рис.3.В соответствует выражению
(23), и модели системы и идентификатора
построены в одном базисе. Поэтому
соответствующие координаты системы и
идентификатора совпадают, т.е.
![]() ,
,
![]() .
.
Опpеделить составляющие матpицы можно и чеpез хаpактеpистические уpавнения. В этом случае исходные данные уравнения (5) могут быть записаны в любом базисе, и вне зависимости от принятого базиса получаем одно и то же характеристическое уравнение. Однако интерпретация результатов расчета все равно требует учета базиса.
Определим хаpактеpистическое уравнение идентификатора, записав матрицы в форме УКП
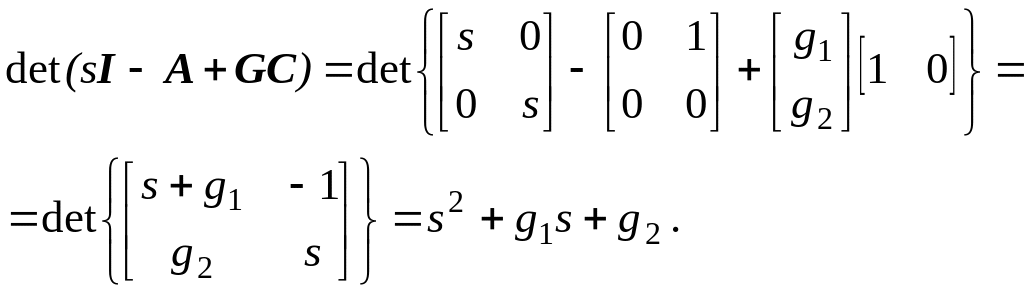
Приравнивая члены при одинаковых степенях полученного хаpактеpистического уравнения и уравнения, определяющего динамику идентификатора
![]() ,
,
имеем,
![]() ;
; ![]() . (24)
. (24)
Решим ту же задачу, записав матрицы в форме ИКП
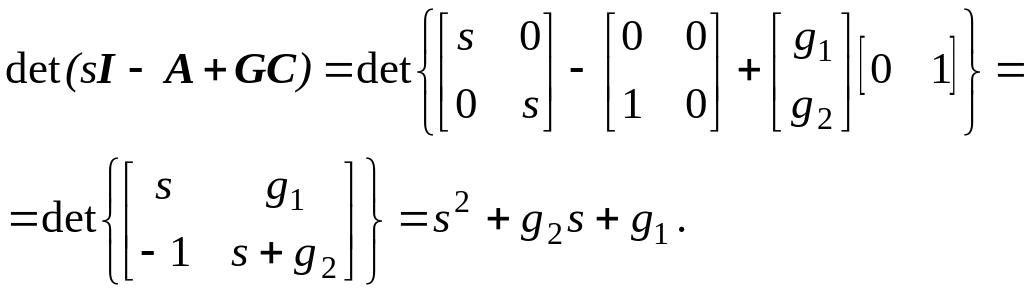
![]() ;
; ![]() . (25)
. (25)
Составление выражений (24) и (25) показывает, что метод определения составляющих матриц через характеристические уравнения, требует дополнительной информации, которая будет использоваться при составлении уравнения, определяющего динамику идентификатора.
Действительно, если не учитывать базисы, в которых представлены матрицы , и , то не ясно как распорядится компонентами матрицы в уравнении. Поэтому целесообразно определять параметры идентификатора с использованием выражения (17) или с помощью формулы Аккермана. В этом случае в процессе решения контролируются применения базисов, что уменьшает вероятность появления ошибки.
