Линейный алгоритм

Линейный алгоритм (следование) состоит из последовательности операций, выполняющихся в порядке их следования.

Фрагмент алгоритма, имеющий линейную структуру.

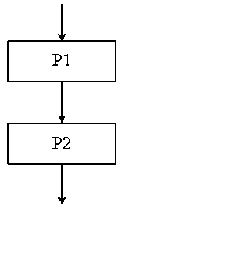
Рис. 1 Линейная структура алгоритма

Линейным называется алгоритм, в котором все действия выполняются строго последовательно.

Рассмотрим примеры составления схем различных алгоритмов.

Пример 1. Даны стороны треугольника , b, c и радиус r вписанной окружности. Требуется вычислить высоту треугольника .

Р е ш е н и е. Площадь треугольника вычисляется по формуле S = pr , где p=( +b+c)/2 - полупериметр.

Определив площадь, можно вычислить высоту треугольника, которая будет равна =2S/ .

Схема алгоритма примера изображенная структурограммами, представлена на рис.2.

Ввод ,b,c,r

Из структурограммы видно, что сначала

Вычислить p

вводятся исходные данные , b, c, r, затем

Вычислить S

вычисляются полупериметр p, площадь S и

Вычислить

высота треугольника . Затем полученное

Печать

Конец

значение выводится на печать. Все вычисления

производятся последовательно одно за другим

и менять их местами нельзя.

Рис.2

Пример 2. Даны переменные A и B. Требуется поменять значения переменных, то есть A присвоить значение B, а B - значение A.

Р е ш е н и е. Введем еще одну промежуточную переменную C. Схема алгоритма примера приведена на рис.3.

В блоке 2 вводятся значения A=1,

A=1; B=5

B=5. В блоке 3 присваиваются

значения: C=1; A=5; B=1.

C=1; A=5;

B=1

На печать выводятся значения

A=5; B=1.Так как переменные

A и B поменяли свои значения,

алгоритм верен.

Рис.3

Разветвляющийся алгоритм

Р азветвляющийся алгоритм содержит точку ветвления (выбора)

(

нет

да

ЛВ

Действие «нет»

Действие «да»

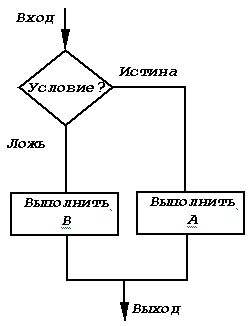
Разветвляющиеся алгоритмы (ветвление).

Алгоритм, в котором в зависимости от заданного условия выполняется та или иная последовательность действий (ветвь) называется разветвляющимся алгоритмом. Условие обычно содержит два арифметических выражения, соединенных знаками отношения такими,

как <, ≤, =, >, ≥, < >.

Например, C<0; X>15; Y=B +D.

В схеме алгоритма проверка условия изображается блоком решения (логическим блоком), представляющим собой ромб. Внутри этого блока записывается заданное условие, а возле выходов блока- Да и Нет. Если условие выполняется, то оно считается истинным и вычислительный поток по выходу Да направляется к следующим блокам. Если условие не выполняется, то оно считается ложным и вычислительный поток направляется к следующим блокам по выходу Нет.

Примеры составления схем разветвляющихся алгоритмов.

Пример 3. Составить схему (рис.4) алгоритма вычисления корней квадратного уравнения .

Р е ш е н и е. Формула вычисления корней квадратного уравнения имеющего в общем случае как вещественные так и комплексные корни хорошо известна и поэтому словестно-формульный способ не приводится.

Алгоритм имеет две ветви. После вычис-

ления в блоке 3 дискриминанта D,

осуществляется проверка его в блоке

D=b²-4ac

решения 4. Если дискриминант больше

нуля, то по выходу Да в блоке 5

Да Нет осуществляется вычисление

вещественных корней уравнения.

В случае, если дискриминант меньше

нуля, то вычисления идут по второй

ветви (по выходу Нет), в которой

вычисляются действительная и

мнимая части корней уравнения.

Рис.4 В блоке 7 (или 8) осуществляется

вывод полученных результатов.

Рассмотрим задачу, когда вычислительный процесс имеет три или более ветвей.

Пример 4. Составить схему (рис.5) алгоритма для вычисления выражения

Р е ш е н и е. Схему алгоритма представим структурограммой.

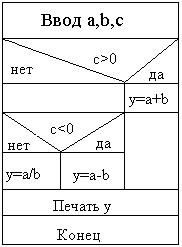После ввода исходных данных (переменных )

проверяется значение переменной в блоке

решения. Если условие выполняется (истинно), то

вычисляется значение переменной .

Полученное значение выводится на печать и

вычисления по этой ветви прекращается.

Если условие ложно, то проверяется значение

переменной в следующем блоке решения.

Рис.5 Если это условие выполняется, то вычисляется

значение переменной и печатается полученное значение . Вычисления прекращаются. Если проверка, осуществляемая блоком решения, показывает, что условие не выполняется, то будет вычислено значение , которое и будет выведено на печать.

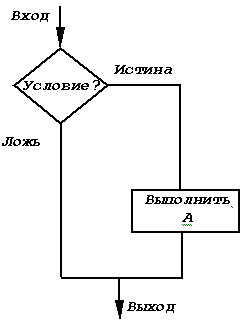
Рис. 2 Разветвляющаяся структура алгоритма	Рис. 3 Структура «неполное ветвление»