Задача №3.

Существует вычислительная система с тремя классами доступных ресурсов. В системе одновременно запущено 5 процессов, каждый их которых использует по несколько экземпляров каждого класса ресурсов 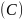. В некоторый момент времени все процессы запрашивают у операционной системы еще определенное количество ресурсов .

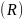Придумайте и запишите минимально возможные значения вектора свободных ресурсов таким образом, чтобы система имела выход из тупиковой ситуации. Рассчитайте значение вектора существующих ресурсов.

Правила формирования матриц и :

Первый столбец матрицы соответствует значениям вашего варианта. Второй столбец соответствует значениям следующего варианта. Третий столбец соответствует значениям варианта с порядковым номером на 2 больше вашего.

Первый столбец матрицы R соответствует значениям варианта с порядковым номером на 3 больше вашего. Второй столбец соответствует значениям варианта с порядковым номером на 4 больше вашего. Третий столбец соответствует значениям варианта с порядковым номером на 5 больше вашего.

Исходные данные:

Решение.

Для получения минимального количества свободных ресурсов, которых должно хватить для выхода системы из состояния взаимоблокировки, возьмём минимальное количество ресурсов:

Если ОС позволит выполнить процесс 3, дав ему все необходимые ресурсы из вектора , то по окончании его он освободит все используемые им ресурсы.

Далее следует предоставить свободные ресурсы процессу 4:

Затем при последовательном выполнении процессов в любом порядке (например: процесс 5, процесс 1, процесс 2) ОС может выйти из состояния взаимоблокировки.

Вектор существующих ресурсов в таком случае будет равен:

Задача №4.

Для той же системы (задача 3) возможны 5 вариантов векторов доступных ресурсов: 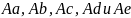. Для каждого значения вектора A запишите порядок предоставления требуемых ресурсов процессам, согласно которому система имеет выход из тупиковой ситуации. Используйте «алгоритм банкира» Дейкстры. Для каждого случая рассчитайте значения вектора существующих ресурсов в системе.

Правила формирования векторов :

Первый элемент векторов соответствует значениям , где — значения вашего варианта таблицы заданий. Второй элемент векторов соответствует значениям следующего варианта. Третий элемент векторов соответствует значениям варианта с порядковым номером на 2 больше вашего.

Исходные данные:

Решение.

При доступных ресурсах невозможен выход из состояния взаимоблокировки из-за нехватки ресурсов. При доступных ресурсах можем выйти из состояния взаимоблокировки различными путями, но первым процессом должен быть или третий, или четвертый. К примеру, или . При вектор существующих ресурсов будет равен , а при – .

Задача №5.

В компьютере с большим количеством устройств запущены 5 процессов ( ) для поиска наличия взаимоблокировок ОС периодически составляет граф Холта для всех ресурсов и процессов.

В определенный момент времени, при анализе состояния процессов, ОС обнаружила, что каждый процесс ранее запросил количество устройств, равное значениям соответственно, и уже получил в пользование количество устройств, равное, соответственно, значениям .

При помощи графов Холка изобразите состояние системы, в которой пять работающих процессов , а количество устройств равно сумме . Пронумеруйте устройства. Расставьте все дуги между процессами и устройствами, а также стрелки направлений на дугах.

Выделите все взаимоблокировки, выпишите последовательности из имен процессов и номеров устройств, находящихся одновременно в состоянии взаимоблокировки. Отдельно выпишите имена процессов, не находящихся в состоянии взаимоблокировок.

Какой из процессов нужно завершить принудительно, чтобы остальные смогли выйти из тупика?

Возможно, ли перегруппировать ресурсы так, чтобы избежать взаимоблокировки?

В какой последовательности должны завершаться процессы, не находящиеся в тупике, чтобы все процессы вышли из заблокированного состояния и продолжили работу?

Исходные данные:

Решение.

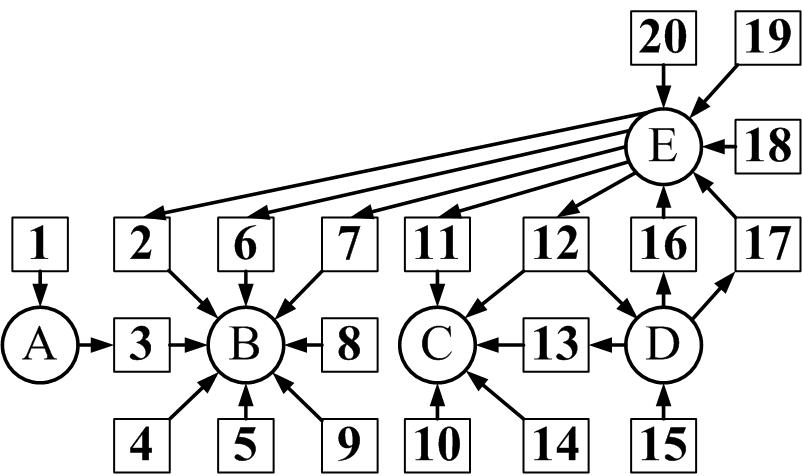
Имеются 2 взаимоблокировки:

• 

• 

Если процесс принудительно завершить, то взаимоблокировки устранятся. Чтобы избежать взаимоблокировок, необходимо иметь граф:

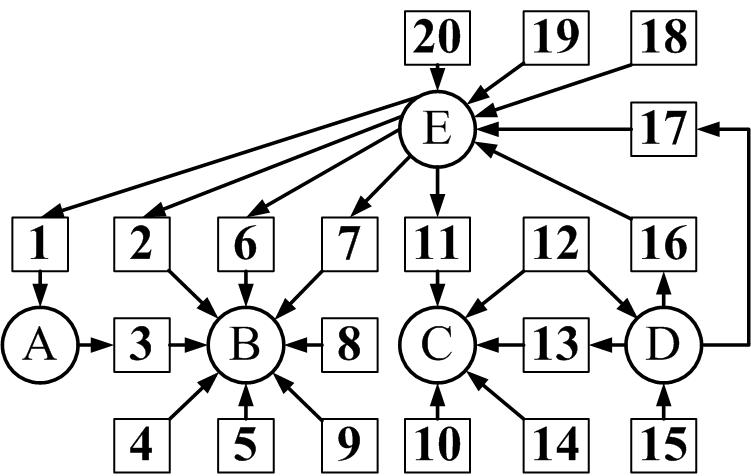
Для успешного завершения всех процессов необходима строгая последовательность некоторых процессов: , а именно: запускается после , а после завершения выполнения , но выполняется строго после .