Лекция 5. Кручение

Кручением называется вид нагружения, при котором к брусу прикладываются внешние скручивающие моменты, а в поперечных сечениях возникает единственный внутренний силовой фактор - крутящий момент M_к (рис.5.1).

 

Б русья, передающие крутящий момент называются валами. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п. В большинстве случаев бывают заданы мощность, передаваемая валом, и числом оборотов, а величины скручивающих моментов определяются исходя из этих данных.

Пусть вал вращается с постоянной скоростью n об/мин. и передает мощность N Нм/с. Угловая скорость вращения вала равна  (рад/сек), а передаваемая мощность .

Скручивающий момент равен .

Построение эпюр крутящих моментов

Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.

Крутящий момент М_к в сечении вала числено равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от сечения, при этом могут рассматриваться как левая, так и правая отсеченные части вала.

Пример 1. Рассмотрим вал, нагруженный скручивающими моментами Т₁=10кНм,   Т₂=25 кНм,   Т₃=35 кНм (рис.5.2).

Воспользуемся методом сечений.

 Рассечем участки вала (рис.5.2). Границами участков являются точки приложения скручивающих моментов.

Отбросим правую отсеченную часть.

Заменим ее крутящим моментом М_к.

Из уравнения равновесия отсеченной части найдем величину крутящего момента М_к, возникающего в сечении.

 

                     Рис.5.2                                                                                                           Рис.5.3

 

I участок

,

M_к1 = 0 .

II участок

,

M_к2 = T₁ = 10 кНм.

III участок

 M_к3 = T₁ +T₂ = 35 кНм.

Для наглядного представления о величине крутящих моментов и характере их распределения по длине вала построим эпюры этих моментов. Построение эпюр крутящих моментов аналогично построению эпюр продольных сил при осевом растяжении-сжатии (рис.5.3).

Заметим, что в местах приложения внешних моментов ординаты эпюры скачкообразно изменяются на величину приложенного внешнего момента.

  

Пример 2. Построить эпюру крутящих моментов для жестко защемленного стержня (рис.5.3.1,а).

Решение.

 Следует отметить, что алгоритм и принципы построения эпюры крутящих моментов полностью совпадают с алгоритмом и принципами построения эпюры продольных сил.

1.Намечаем характерные сечения.

2.Определяем крутящий момент в каждом характерном сечении.

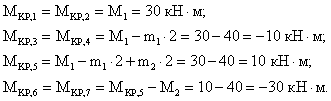
3.По найденным значениям строим эпюру (рис.5.3.1,б).

Рис.5.3.1

Напряжения в поперечном сечении

Опыты показывают, что если на поверхности бруса круглого сечения нанести прямоугольную сетку, а на торцевой поверхности нанести радиальные линии (рис.5.4), то после деформации кручение окажется что:

 все образующие поворачиваются на один и тот же угол , а прямоугольники, нанесенные на поверхности, превращаются в параллелограммы;

 торцевые сечения остаются круглыми, плоскими, расстояния между ними не меняются;

 каждое сечение поворачивается относительно другого на некоторый угол , называемый углом закручивания;

 радиальные линии на торцевой поверхности остаются прямыми.

На основании этих наблюдений можно заключить, что может быть принята гипотеза Бернулли (гипотеза плоских сечений), а в вале возникают условия чистого сдвига, в поперечных сечениях действуют только касательные напряжения, нормальные напряжения равны нулю.

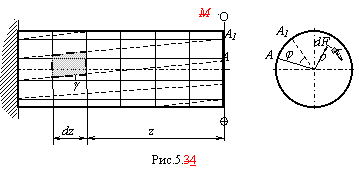
Рассмотрим поперечное сечение вала, расположенное на некотором расстоянии z от торцевого, где М_к= T (рис.5.4). На элементарной площадке dF будет действовать элементарная сила dF, момент который относительно оси вала равен (dF). Крутящий момент М_к, в сечении равен

.                                          (5.1)

Для того чтобы проинтегрировать это выражение необходимо знать закон распределения напряжений в сечении. Выделим из вала элементарное кольцо длиной dz и толщиной d (рис.5.5).

Правый торец элемента повернется относительно левого на угол d, образующая СВ повернется на угол  и займет положение СВ₁. Угол  - относительный сдвиг. Из треугольника ОВВ₁ найдем:

.

 Из треугольника СВВ₁: . Откуда, приравнивая правые части, получим

.

На основании закона Гука при сдвиге:

.                                     (5.2)

Подставим выражение (5.2) в (5.1):

.

Откуда

.                                        (5.3)

Подставим значение  в выражение (5.2) получим:

.

Таким образом, касательные напряжения при кручении прямо пропорциональны расстоянию от центра тяжести сечения до рассматриваемой точки и одинаковы в точках, одинаково удаленных от центра тяжести сечения (рис. 5.6). При  = 0 получим  = 0. Наибольшие напряжения возникают в точках контура сечения при  = R:

.

Величина отношения полярного момента инерции к радиусу вала называется моментом сопротивления сечения при кручении или полярным моментом сопротивления

.

Для сплошного круглого сечения

.

Для кольцевого сечения

,

где .

 

Тогда максимальные касательные напряжения равны

.