**************************************************Тема 1

Покажемо, що СВФ можна представити у вигляді гармонічних коливань з випадковими амплітудами і випадковими фазами:

Розглянемо ВФ:

Перетворимо ВФ

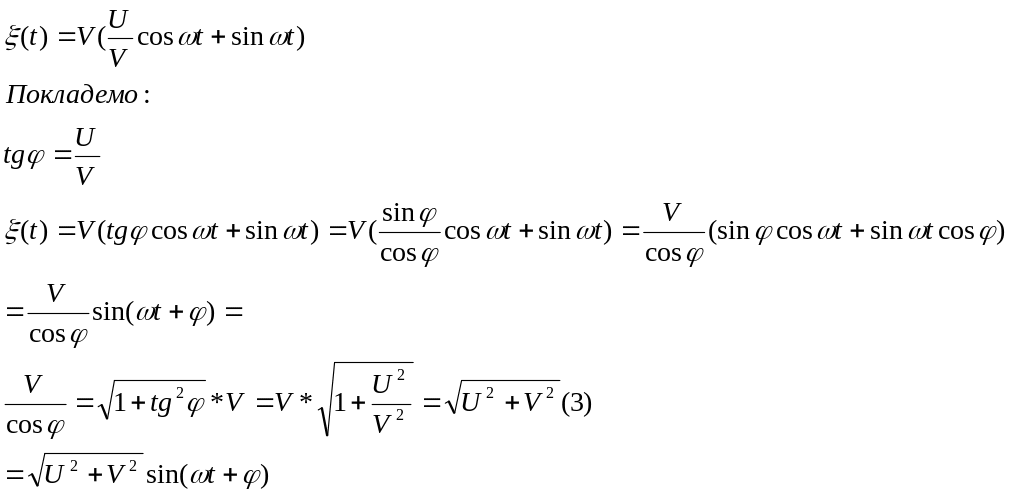
ВФ (1) можна тлумачити як гармонічне коливання з амплітудою (3) та випадковою фазою

де частота.

Покажемо що ВФ (1) є стаціонарною

1. Враховуючи , що можемо зробити висновки , що математичне сподівання ВФ = 0,

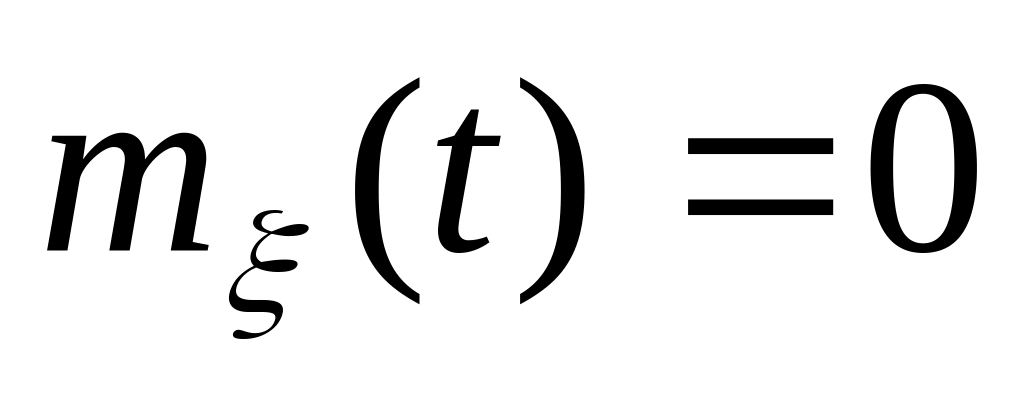
2. Знайдемо кореляційну функцію

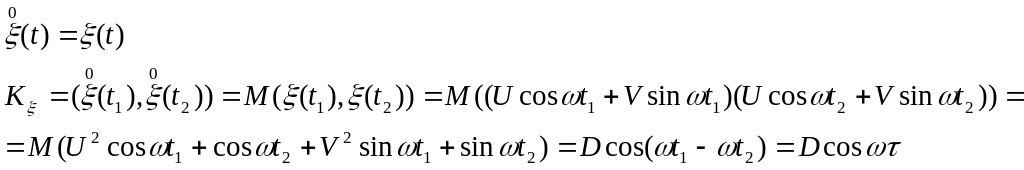
ВФ (1 ) є стаціонарною у великому розумінні.

Розглянемо ВФ яка є сумою скінченного числа доданків виду (1)

(4)

Попарно некорельовані

Доведемо що дана ВФ (4) є стаціонарною

1. математичне сподівання кожного із доданків ВФ (4)=0, тоді математичне сподівання суми =0

2. Оскільки

Якшо доданок суми (4) є попарно не корельовано то кореляційна функція цієї суми = сумі кореляційної функції доданків..Таким чином перевіримо що наші доданки є попарно некорельовані.

Для простоти не втрачаючи цілісності обмеження двома доданками

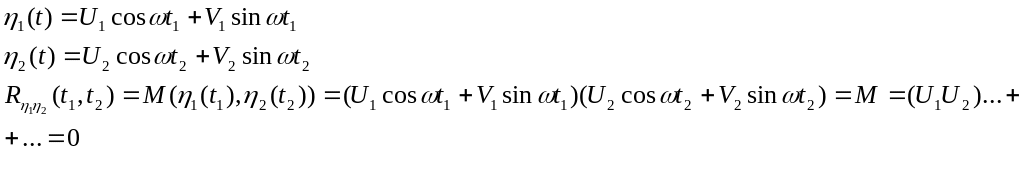
Отже доданки не корельовано. А кореляційна функція буде

Враховуючи що для кожного із доданків ВФ (4) справедливе представлення то можна записати

ВФ може бути представлена у вигляді суми гармонік різних частот та фаз.

Спектральним розкладом СВФ називається представлення цієї функції у вигляді суми гармонічних коливань ріщних частот з випадкими амплітудами і випадковими фазами

******************************************* Тема 2

(7)

Дисперсія СВФ, що представлена у вигляді скінченної кількості гармонік = сумі дисперсій гармонік,які її складають

Дискретним спектром СВФ називається сума дисперсій гармонік,які її складають. Спектр можна представити графічно.

Розглянемо випадок рівновіддалених част. Множина яких зліченна (нескінченна)

Спектральний розклад (8)

, де Т-дійсне додатнє число.

Кореляц.Ф-я стац вп (8):

де r=t2-t1 (9)

Враховуючи що отримаємо (10)

Дисп може бути предст у вигляді (8),визначається як сума дисперсій і їх гармонік

Відмітимо, що (9) можна розглядати кореляц ф-ю в ряд Фурє по косинусу.

(11)

Маючи (9)видно що кор. ф-я це період ф-ї з періодом rT і коефіцієнт Фурє визначається як (11) або (12): (12)

СПЕКТРАЛЬНІ ЩІЛЬНОСТІ СТАЦІОНАРН ВФ називається ф S(w) яка

з‘вязана з кореляц функцією взаємн обернено перетворю Фур’є

(13)

(14)

Ці ф-ї (13 і 14) називаються Віннера-Хінчена. У дійсній формі вони представляють собою взаємно оберкосинус перетвор ф-ї:

(15)

(16)

Враховуючи що та маємо: (17)

Частину інтервалу відповідає дисперсія 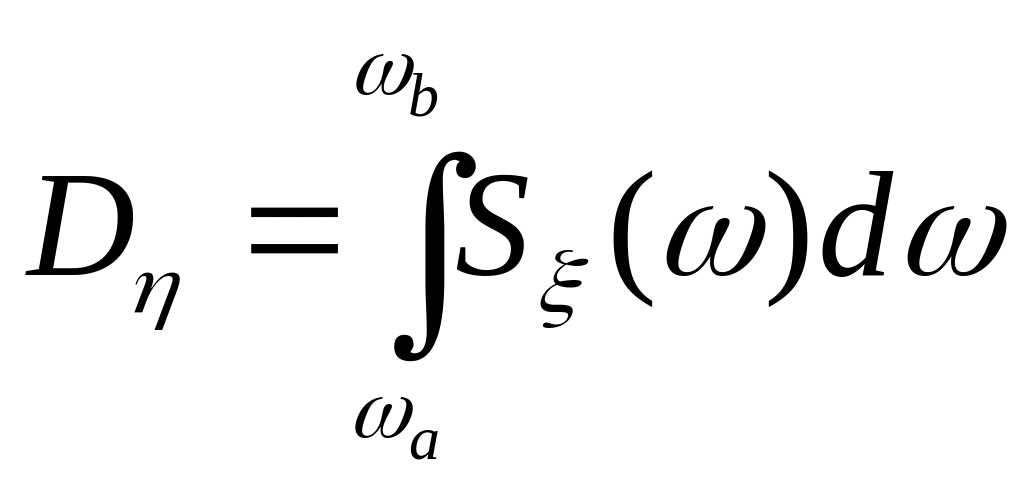(18)

Отже спектр щільність описує розп дисперсію стац ВФ за част,що неперервно замкнена. Вона є невід’ємною фінкцією

**************************************Тема 3

4)Нормована спектральна щільність:

S _ ( )=

У вигляді косинус-перетворення Фур’є:

S _норм ( )=

Через нормовану спектральну щільність:

_ ( )=

5) Нехай (t) i (t) стаціонарні і стац-звязані випадкові ф-ї,що мають взаємокореляційну ф-ю r _ ( )

Тоді взаємною спектральною щільністю 2-х стаціонарних ф-й (t) i (t) називають ф-ю:

S _ (

r _ ( )

6) Узагальнена ф-я –це границя послідовності одно параметричного сімейства неперервної ф-ї.

Дельта-ф-я визначається тією умовою, що вона ставить у відповідність будь-які неперервні ф-ї f(t) її значення при t=0.

,

_E (t)=

Враховуючи,що _E (t) _E (t)

умовно пишуть

Дельта ф-ю можна представити інтегралом Фур’є:

Звідси:

7) Стаціонарний білий шум назив. Стац. Випадкову ф-ю (t) спектральна щільність якої є S ( )=S=const

Кореляційна ф-я білого шуму:

k _ (

k _ ( =2

де 2 - інтенсивність стац. білого шуму.Кореляційна ф-я білого шуму пропорційна дельта ф-ї

8)Стац. лінійною динамічною системою назив. С-му, яка описується лінійним диференціальним рівнянням зі сталими коефіцієнтами виду:

a ₀ Y ⁽ⁿ⁾ (t)+ a ₁ Y ^(n-1) (t)+…+ a _n Y (t)= b ₀ X ^(m) (t)+ b ₂ X ^(m-1) (t)+…+ b _n X (t)

де Х(t)-вхідна стац. вип. ф-я

Y(t)- вихідна стац. вип. ф-я

*******************************************Тема 4

Частотною характеристикою лінійної динамічної системи називають: (40)

(41)

(42)

(43)