2.Техническое задание.

2.1.Анализ предметной области.

Предлагается разработать калькулятор для матричных вычислений, следовательно предметной областью будет являться теория матриц. Теория матриц нашла огромное применение в решении систем линейных уравнений и не только, поэтому целесообразно было бы создать такой калькулятор.

2.1.1 Матрицы

Матрицей называется прямоугольная таблица, заполненная некоторыми математическими объектами, например, числами, векторами, функциями, производными, интегралами, операторами и т.д. Будем рассматривать матрицы с элементами из поля действительных чисел, хотя все рассуждения сохраняются и для матриц с другими элементами.

Чаще всего элементы матрицы обозначаются одной буквой с двумя индексами, указывающими "адрес" элемента - первый индекс дает номер строки, содержащий элемент, второй - номер столбца. Если матрица имеет m строк и n столбцов, то говорят, что матрица имеет размеры . Принято обозначать матрицы заглавными латинскими буквами, часто - полужирными, а ее элементы - такими же буквами, но строчными. Таким образом, матрица (размеров ) записывается в виде

.

Для краткости допускается обозначение матрицы размеров в виде, где индекс i пробегает все значения от 1 до m, а j - от 1 до n. При обозначении матриц используются скобки - круглые и квадратные.Матрицы, имеющие одно и то же число n строк и столбцов, называютквадратными; это число n называют порядком квадратной матрицы. Важную роль играют так называемые диагональные матрицы. Под этим подразумеваются квадратные матрицы, имеющие все элементы равные нулю, кроме элементов главной диагонали, т.е. элементов в позициях (1,1), (2,2), ..., (n,n). Диагональная матрица D с диагональными элементами d₁, d₂, ..., d_n обозначается diag(d₁, d₂, ..., d_n). Диагональная матрица diag(1, 1, ..., 1) называется единичной и обозначается E (или E_n) или же I (или I_n). Матрица, состоящая из одних нулей, называется нулевой.Матрица, состоящая из одной строки, часто называется вектором (строкой, вектор-строкой, строчной матрицей), а из одного столбца - вектор-столбцом (столбцом, столбцовой матрицей).Две матрицы считаются равными, если они одного размера и у них совпадают элементы, стоящие на одинаковых местах.Матрицу A={a_{i j}} можно транспонировать, т.е. заменить строки столбцами, в результате чего получится транспонированная матрица A^T={a_{j i}}.Две матрицы A={a_{i j}} и B={b_{i j}} одного и того же размера можноскладывать, их суммой будет матрица того же размера C={c_{i j}}, , т.е. чтобы получить сумму двух матрицы достаточно сложить соответствующие элементы этих матриц, находящихся на одних и тех же позициях. Поскольку мы рассматриваем здесь матрицы с элементами из поля P действительных чисел, то очевиднаассоциативность операции сложения матриц, вытекающая из ассоциативности сложения элементов поля P. Аналогично имеет место коммутативность сложения. Таким образом, справедливы действия:

1. (A+B)+C=A+(B+C); [Ассоциативность]

2. A+B=B+A; [Коммутативность]

3. Матрица 0, состоящая из нулей, играет роль нуля: A+0=A при любой A.Определим произведение элемента c из поля P на матрицу A={a_{i j}}: cA={ca_{i j}}, т.е. чтобы умножить матрицу на число необходимо каждый элемент матрицы умножить на это число.Для любой матрицы A существует противоположная матрица -A такая, что A+(-A)=0. 

В качестве матрицы -A, очевидно, следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.

4. .

5. .

6. .

7. .

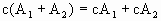Все перечисленные свойства матриц непосредственно следуют из определений и свойств действий в поле чисел.Рассмотрим матрицу A={a_{i j}} размером и матрицу B={b_{i j}} размером . Число столбцов первой матрицы (стоящей слева в произведении) равно числу строк второй матрицы (стоящей справа в произведении). Для матриц, обладающих таким свойством, можно ввести действиеумножения матрицы на матрицу. В результате получается матрица C={c_{i j}} размером , где. Правило умножения легко запомнить в словесной форме:  "чтобы получить элемент произведения c_{i j} двух матриц нужно элементы i-ой строки первой матрицы умножить на соответствующие элементы j-го столбца второй матрицы и все произведения сложить". Это правило называют "правилом строка на столбец".

Пример:

Пусть A={a_{i j}} размером и B={b_{i j}} размером , а также введем векторы,и. Рассмотрим линейные подстановки с этими матрицами:

и

.

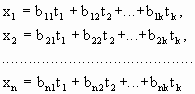Эти подстановки, используя определение умножения матриц, можно записать в матричном виде: Y=AX, X=BT.Покажем, что если эти две подстановки сделать одну за другой, т.е. выразить переменные y₁, ..., y_m через t₁, ..., t_k, то матрица коэффициентов окажется равной AB.

Действительно, пусть

.

Тогда коэффициент c_{i j} есть коэффициент при t_j в y_i. Выпишем все необходимое для вычисления этого коэффициента:

.

При подстановке x₁, x₂, ..., x_k в y_i, получим

.

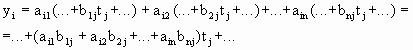Таким образом, , так что матрица коэффициентов в выражениях y₁, ..., y_m через t₁, ..., t_k действительно равна AB.  Итак, последовательному произведению ("суперпозиции") двух линейных подстановок соответствует произведение их матриц. В матричной форме суперпозицию этих подстановок можно записать в виде Y=A(BT). Вместе с тем матрица суперпозиции равна AB, и этот факт записывается так: Y=(AB)T. Таким образом, верно следующее соотношение ассоциативности:

A(BT)=(AB)T, где T - столбец.

Рассмотрим теперь свойства действия умножения матриц:

1. (cA)B=A(cB)=cAB;

2. (A₁+A₂)B=A₁B+A₂B;

3. A(B₁+B₂)=AB₁+AB₂.

Эти свойства непосредственно вытекают из того, что элементы произведения выражаются как через элементы A, так и через элементы B в виде линейных однородных многочленов. Это можно проверить, используя правило умножения и сложения матриц, группируя необходимые слагаемые).

4. (AB)C=A(BC) [ассоциативность умножения].

Это свойство трактуется таким образом, что если одна из частей равенства имеет смысл, то имеет смысл и другая, и они равны. Это равенство можно доказать, воспользовавшись следующим простым замечанием. Пусть P и Q - две матрицы такие, что PQ имеет смысл. Пусть Q₁, Q₂, ..., Q_k - столбцы матрицы Q. Тогда столбцами матрицы PQ являются PQ₁, PQ₂, ..., PQ_k, что непосредственно следует из определения. Это обстоятельство можно записать в виде P(Q₁, Q₂, ..., Q_k) = (PQ₁, PQ₂, ..., PQ_k).

Обозначим через C₁, C₂, ..., C_l столбцы матрицы C. Тогда (AB)C = ((AB)C₁, (AB)C₂, ..., (AB)C_l). Далее, BC = (BC₁, BC₂, ..., BC_l) и A(BC) = (A(BC₁), A(BC₂), ..., A(BC_l)). Но как было установлено выше, (AB)C₁ = A(BC₁), (AB)C₂ = A(BC₂), ..., ибо C₁, C₂, ... - столбцы. Таким образом, (AB)C = A(BC).

Особую роль при умножении матриц играют единичные матрицы E_n (если нужно буквой n указать порядок) или просто E. Из правила умножения матриц непосредственно следует, что AE=A и EA=A, если эти произведения определены.

5. (AB)^T=B^TA^T. Об этом свойстве произведения матриц говорят так: "при транспонировании произведения матриц порядок сомножителей меняется".

Докажем это. 

Пусть ,.

Положим ,, так что,.

Пусть, далее, ,.

Тогда ,.

Итак, при всех i = 1, 2, ..., m и j = 1, 2, ..., n, а это и означает, что G=F^T, т.е. , что и требовалось доказать.Таким образом, матрицы можно складывать, умножать их на число, а также умножать матрицы друг на друга. Эти действия обладают свойствами:

1. (A+B)+C=A+(B+C);

2. A+B=B+A;

3. Существует 0: A + 0 = 0 + A = A;

4. Для A существует -A: A + (-A)=0;

5. .

6. .

7. .

8. .

Если для некоторых объектов (в нашем случае, это матрицы) выполняются эти восемь свойств, то говорят, что эти объекты  образуют векторное пространство, так что матрицы фиксированных размеров образуют векторное пространство.

9. (AB)C=A(BC).

10. (cA)B=A(cB)=cAB.

11. (A₁+A₂)B=A₁B+A₂B.

12. A(B₁+B₂)=AB₁+AB₂.

13. Существуют единичные матрицы (единицы), а именно, если A размером , то E_mA = AE_n = A.

14. (A^T)^T = A.

15. (A + B)^T = A^T + B^T.

16. (cA)^T = cA^T.

17. (AB)^T = B^TA^T.

Для квадратных матриц фиксированного порядка n действия сложения и умножения определены всегда, и их результатами являются квадратные матрицы того же порядка. Об этом обстоятельстве говорят таким образом: квадратные матрицы фиксированного порядка образуют кольцо. Кольцо, наделенное структурой векторного пространства, т.е. система объектов, обладающих свойствами 1-12, называется алгеброй над основным полем. Таким образом, квадратные матрицы с элементами из поля K составляют алгебру над этим полем.