1.3. Однопродуктовая бездефицитная статическая модель с дисконтом

На практике поставщики нередко предлагают систему скидок (дисконтов), чтобы заинтересовать покупателя в приобретении крупной партии товара. Предлагаемая модель управления запасами учитывает возможность такого рода дисконта.

Пусть справедливы все обозначения и условия раздела 1.1, за исключением того, что на приобретаемый ресурс имеется дисконт в зависимости от объема заказа. Цена единицы ресурса зависит от размера заказа и определяется формулой:

Точка разрыва цены предполагается известной величиной.

Суммарные затраты за цикл помимо издержек хранения, оформления и размещения заказа, должны включать издержки приобретения. Суммарные затраты в единицу времени равны

(1.3)

Пусть значение размера заказа, задаваемое формулой Уилсона. Определим числовой параметр с помощью уравнения с дополнительным условием и рассмотрим следующие три области:

; ; .

Оптимальный размер заказа зависит от того, в какой области лежит точка разрыва цены и определяется следующим образом:

Пример 1.4. В условиях задачи примера 1.1 предположим, что покупная цена насосов зависит от объема приобретаемой партии. Схема дисконтирования цены определяется следующей таблицей:

	Вариант 1	Вариант 2	Вариант 3	Вариант 4	Вариант 5	Вариант 6
Величина заказа, штук	Менее 500	500-999	1000-1999	2000-4999	5000-9999	Свыше 10000
Цена за штуку, $	100	98	96	94	92	90

Требуется определить оптимальную величину заказа, а также длину цикла заказа.

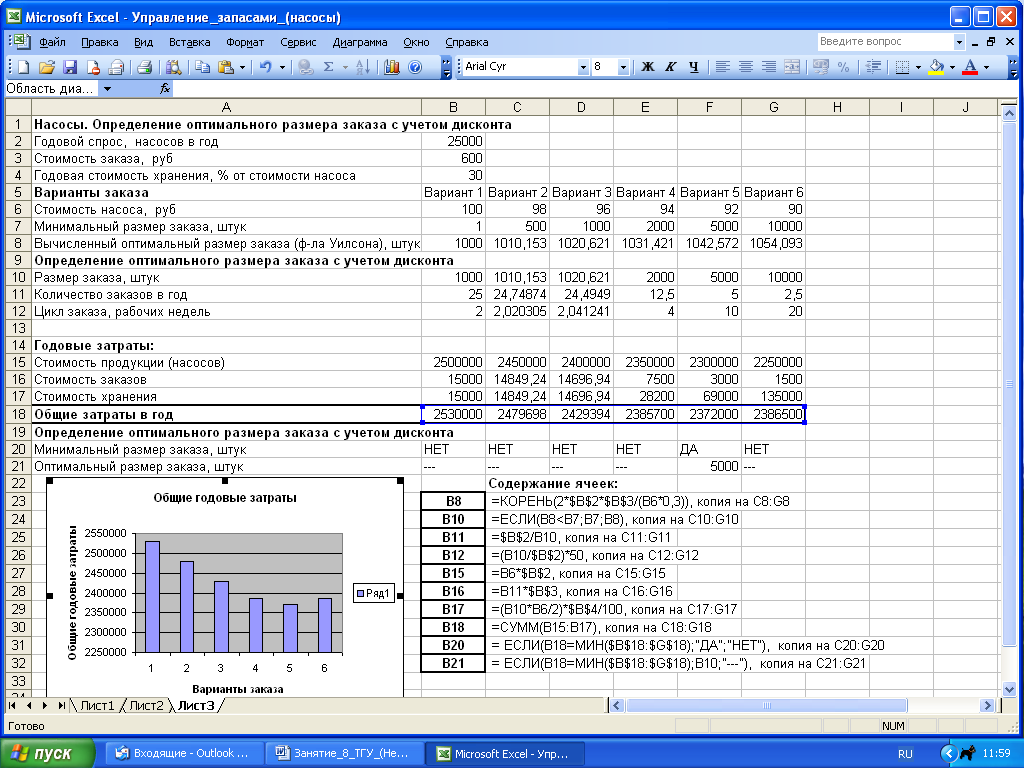
Рис. 1.3. Фрагмент рабочего листа Excel с решением задачи примера 1.4

Задачи для самостоятельного решения

Тема 2: различные задачи нелинейного программирования, связанные с функциями затрат и производственной функцией

Пример 2.1. Производственная функция фирмы (производственная функция выражает объем выпускаемой фирмой продукции) имеет следующий вид:

,

где затраты ресурсов. Цена покупки фирмой единицы ресурсов равна 5 и 10 у.е. соответственно. Каков наибольший выпуск при общих издержках ?

Решение. Имеем задачу нелинейного программирования

Шаблон с решением представлен на рис. 2.1:

Рис 2.1. Шаблон с решением задачи примера 2.1

Ответ: 66,66667 при 6,666667

Задачи для самостоятельного решения

2.1. Производственная функция фирмы имеет следующий вид:

,

где затраты ресурсов. Определить максимальный выпуск и обеспечивающие этот выпуск затраты ресурсов при условии, что . Каковы предельные продукты в оптимальной точке?

Ответ: 15 при .

2.2. Производственная функция фирмы описывается функцией Кобба-Дугласа:

,

где А=0,75 – технологический коэффициент, x– затраты капитала, y – суммарные затраты ресурсов. Найти значения величин x и y при ценах используемых ресурсов соответственно , чтобы при фиксированном объеме выпускаемой продукции обеспечивался минимум затрат , выражаемых формулой

.

При поиске решения принять ; .

Ответ: C_min=188561,8 при .

2.3. Достоверно установлено, что недельная прибыль фирмы определяется формулой

,

где затраты ресурсов первого и второго типов соответственно. Определить оптимальный расход ресурсов, при котором прибыль была бы максимальной, при условии, что себестоимости единицы ресурса первого и второго типов соответственно равны , а недельный бюджет фирмы, отведенный на суммарные затраты ресурсов определен в размере 15000.

Ответ: 100072,4 при 5,172414, 8,275862.

2.4. Фирма, выпускающая химическую продукцию, продает три вида продукции: . Установлено, что функция дохода фирмы имеет вид , где представляют собой месячные нормы выработки первого, второго и третьего вида продукции соответственно. На основе анализа графиков распределения уровней спроса на выпускаемую продукцию фирмой выявлены следующие предельные условия норм выработки упомянутых выше видов продукции:

Кроме того, фирма должна иметь в виду, что объемы имеющихся в наличии сырьевых материалов ограничены; это приводит к следующим ограничениям, которые должны учитываться при составлении производственного графика:

Составьте наиболее рациональный для данной фирмы план производства и определите максимальное значение функции суммарного дохода фирмы.

Ответ: .