
- •Интегральное исчисление функций одной переменной
- •I. Неопределенный интеграл
- •§1. Первообразная
- •§2. Свойства неопределённого интеграла
- •§3. Основная таблица интегралов
- •§4. Основные методы интегрирования
- •I. Метод введения нового аргумента
- •II. Метод подстановки
- •III. Интегрирование по частям
- •§5. Интегрирование рациональных выражений
- •1. Основные понятия
- •2. Интегрирование простейших дробей.
- •3. Разложение правильной рациональной дроби на сумму простейших
- •4. Интегрирование рациональной функции
- •§6. Интегрирование иррациональных функций
- •§7. Интегрирование выражений, содержащих тригонометрические и показательную функции
- •II.Частные случаи
- •II. Определенный интеграл
- •§1. Понятие определённого интеграла
- •§2. Нижние и верхние интегральные суммы
- •§3. Некоторые классы интегрируемых функций
- •1. Интегрируемость непрерывных функций
- •2. Интегрируемость монотонной функции
- •3. Интегрируемость функций, имеющих конечное число точек разрыва
- •§4. Основные свойства определённого интеграла
- •§5. Определённый интеграл с переменным верхним пределом. Существование первообразной функции. Формула Ньютона-Лейбница
- •§6. Интегрирование по частям и замена переменной в определённом интеграле. Интегрирование чётных и нечётных функций
§5. Интегрирование рациональных выражений
1. Основные понятия
Определение.
Рациональной
функцией
(или рациональной
дробью)
называется функция вида
![]() =
=
![]() ,
где Pn,
Qm
– многочлены степеней n
и m
соответственно. Если n<m,
то рациональная дробь называется
правильной,
в противном случае (n≥m)
– неправильной.
,
где Pn,
Qm
– многочлены степеней n
и m
соответственно. Если n<m,
то рациональная дробь называется
правильной,
в противном случае (n≥m)
– неправильной.
Если рациональная
дробь неправильная, то её с помощью
деления можно представить в виде суммы
многочлена (целая часть) и правильной
рациональной дроби, т.е.
 =
=![]() +
+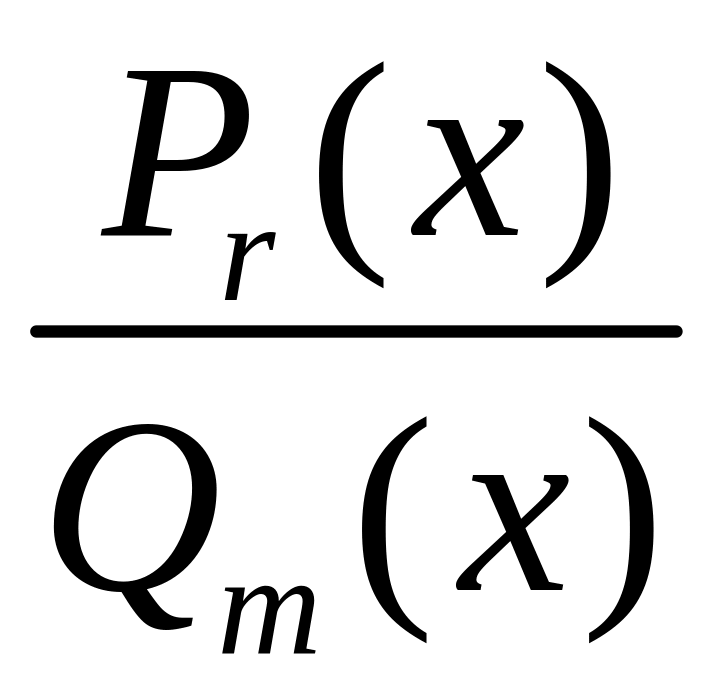 ,
где Pn-m(x)
– многочлен степени n
– m,
r
<m
.
,
где Pn-m(x)
– многочлен степени n
– m,
r
<m
.
Примеры.
1) Метод деления
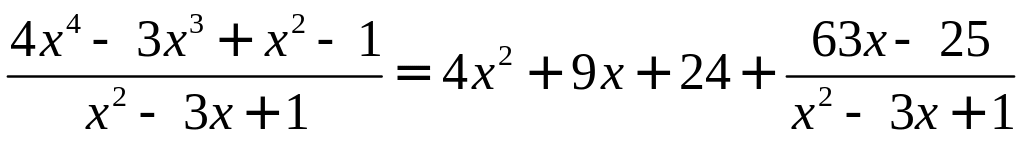
4 x4–
3x3+
x2
–
1 x2
-
3x+
1
x4–
3x3+
x2
–
1 x2
-
3x+
1
4 x4–12x3+4x2
4x2
+9x+24
x4–12x3+4x2
4x2
+9x+24
 9x3
– 3x2
- 1
9x3
– 3x2
- 1
 9x3–27x2
+ 9x
9x3–27x2
+ 9x
24x2 – 9x – 1
24x2–72x + 24
 63x
– 25
63x
– 25
2) Метод преобразований
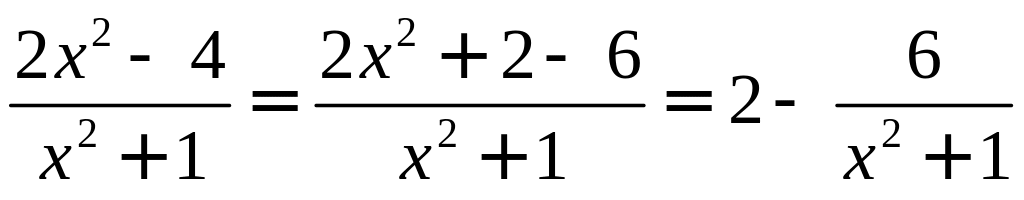 .
.
2. Интегрирование простейших дробей.
Определение. Простейшими дробями называются дроби следующих четырёх типов:
1)
![]() ; 2)
; 2) ; 3)
; 3) ; 4)
; 4)
 ,
,
где A,
M,
N,
a,
p,
q
![]() ,
трехчлен
,
трехчлен
![]() не имеет действительных корней (т. е.
D=p2–4q<0).
не имеет действительных корней (т. е.
D=p2–4q<0).
1)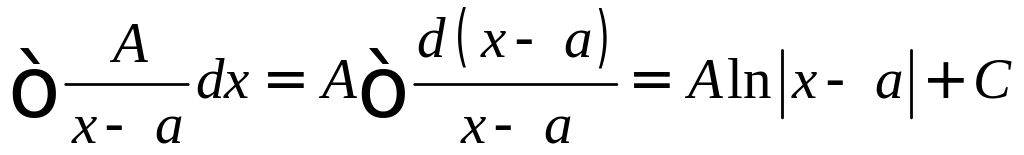 ;
;
2)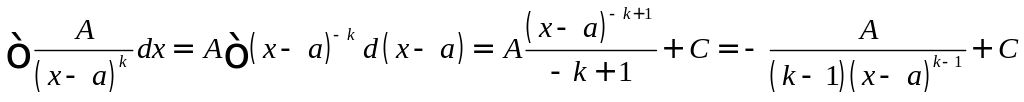 ;
;
3)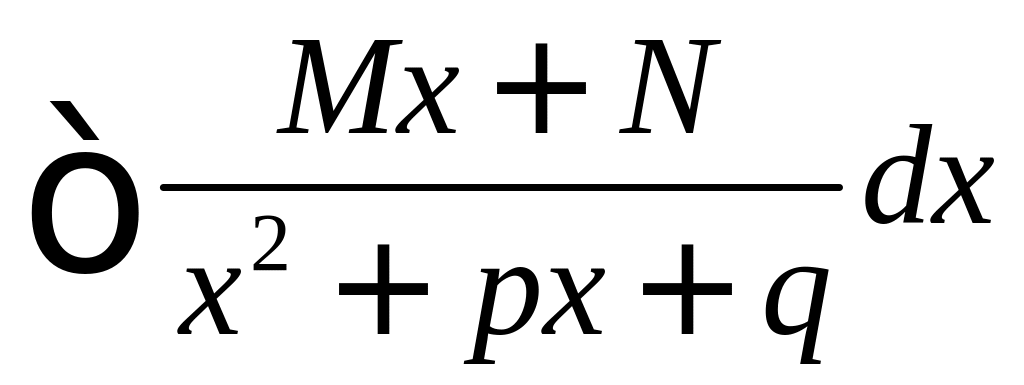 .
.
В числителе выделяется выражение равное производной знаменателя. Разделив затем почленно, получим табличный интеграл и интеграл вида
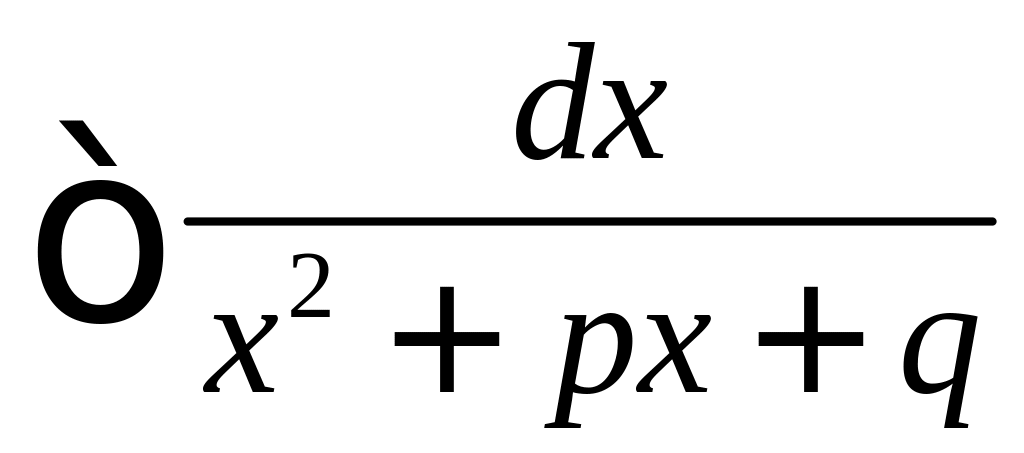 ,
который вычисляется путём выделения
полного квадрата в знаменателе.
,
который вычисляется путём выделения
полного квадрата в знаменателе.
Пример.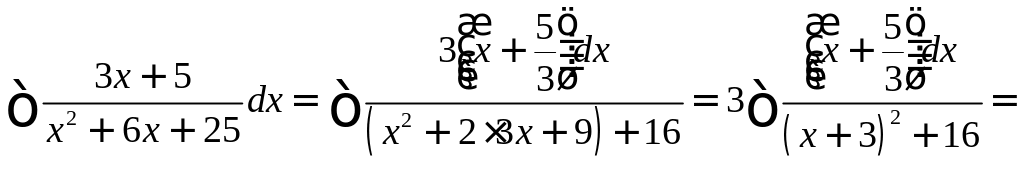

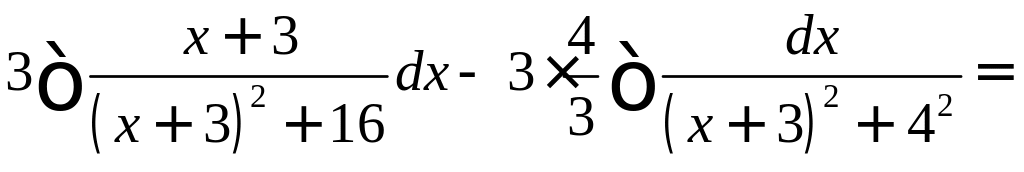

![]() .
.
4)
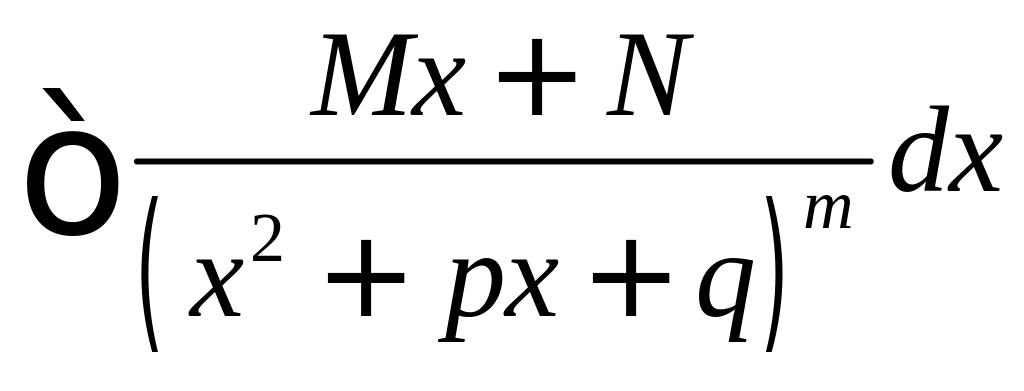 вычисляется
аналогично интегралу вида 3) с применением
рекуррентной формулы (7).
вычисляется
аналогично интегралу вида 3) с применением
рекуррентной формулы (7).
3. Разложение правильной рациональной дроби на сумму простейших
Пусть
![]() - правильная рациональная дробь, Q(x)
– многочлен степени n
с коэффициентом перед старшей неизвестной
равным единице (для простоты):
Q(x)=xn+b1xn-1+…+bn.
Q(x)
имеет n
действительных и комплексных корней.
Так как у Q(x)
коэффициенты – действительные числа,
то комплексные корни попарно сопряжены.
- правильная рациональная дробь, Q(x)
– многочлен степени n
с коэффициентом перед старшей неизвестной
равным единице (для простоты):
Q(x)=xn+b1xn-1+…+bn.
Q(x)
имеет n
действительных и комплексных корней.
Так как у Q(x)
коэффициенты – действительные числа,
то комплексные корни попарно сопряжены.
Если a1, a2, … an – действительные корни Q(x), то Q(x)=(x–a1)(x–a2)… (x-an).
Может быть, что a1=a2=…=ak=a, тогда Q(x)=(x-a)k(x-ak+1)… (x-an), т.е. если а – корень крайности к, то в разложении присутствует множитель (x-a)k.
Если l+ki и l–ki – сопряжённые комплексные корни, то
(x-(l+ki))(x-(l-ki))=((x-l)+ki)((x-l)-ki)=(x-l)2-(ki)2=x2-2lx+l2+k2=x2+px+q,
![]() .
Следовательно, сопряжённым комплексным
корням соответствует в разложении Q(x)
квадратный трёхчлен с действительными
коэффициентами.
.
Следовательно, сопряжённым комплексным
корням соответствует в разложении Q(x)
квадратный трёхчлен с действительными
коэффициентами.
Если l+ki и l–ki – корни кратности m, то в разложении Q(x) будет присутствовать множитель (x2+px+q)m.
Теорема 1. Если Q(x) – многочлен степени n с действительными коэффициентами, то его можно единственным образом разложить на линейные и квадратичные множители с действительными коэффициентами.
Если a1,
a2,
…, an
– действительные корни кратности m1,
m2,
…, mr
соответственно,
![]() – комплексные корни кратности μ1,
μ2,
…, μs
соответственно, то разложение Q(x)
на неприводимые множители имеет вид:
– комплексные корни кратности μ1,
μ2,
…, μs
соответственно, то разложение Q(x)
на неприводимые множители имеет вид:
![]()
![]() (1),
(1),
где
![]() .
.
Теорема 2. Если - правильная рациональная дробь, а разложение Q(x) на неприводимые множители имеет вид (1), то справедливо разложение:
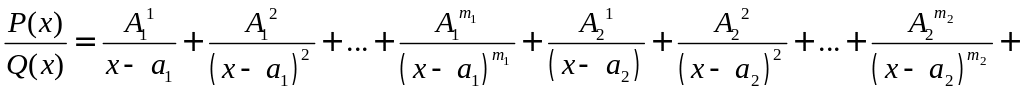

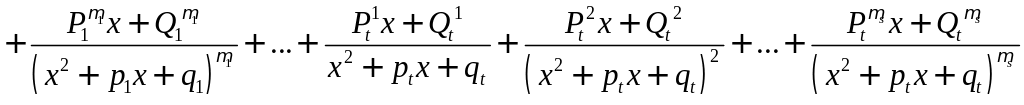 .
(2)
.
(2)
Теорема 2 утверждает, что любую рациональную дробь можно представить в виде суммы конечного числа простейших дробей.
Вычисление коэффициентов разложения
I. Метод неопределённых коэффициентов
По виду многочленов знаменателя правильной рациональной дроби пишут для этой дроби разложение (2) с буквенными коэффициентами. Затем в правой части разложения дроби приводят к общему знаменателю. В результате получают две тождественно равные дроби с одинаковыми знаменателями. Приравнивают числители:
P(x)=c1xn-1+c2xn-2+…+cn-1х+cn. (3)
Приравнивая коэффициенты при равных степенях x, получают систему из n линейных уравнений с n неизвестными c1, c2,…, cn. Решая её, находят c1, c2,…, cn и подставляют в разложение (2). В силу теоремы 2 это разложение единственно.
Пример.
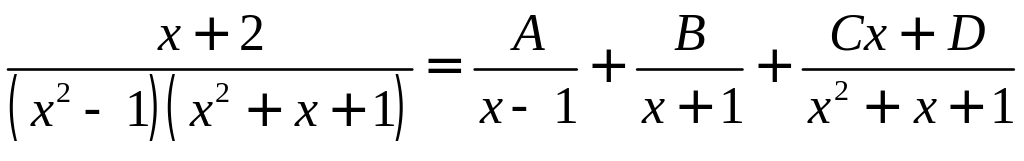 .
.

![]() ;
;
![]() .
.

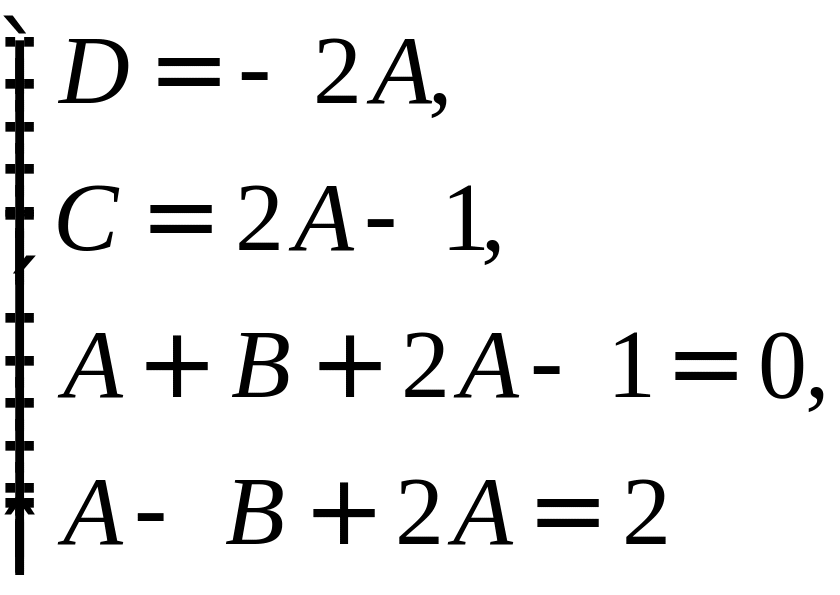
![]()
![]()
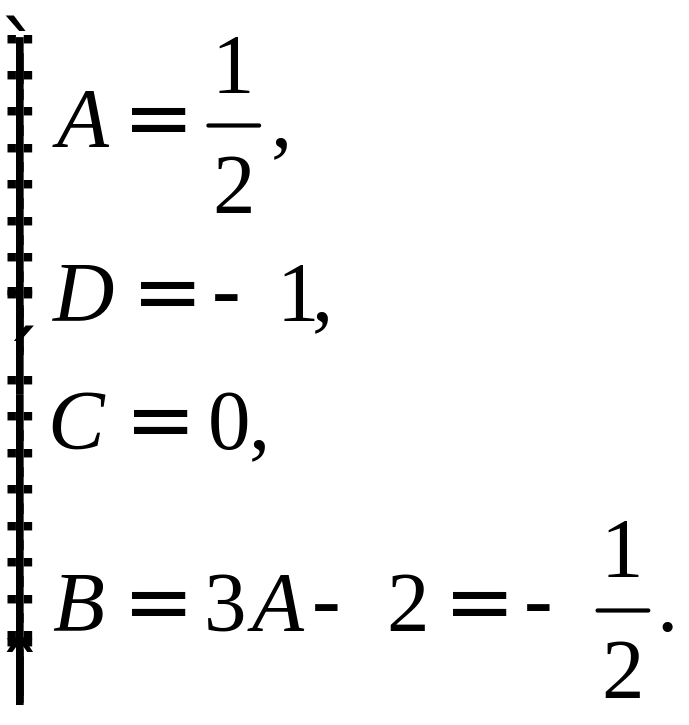
Тогда
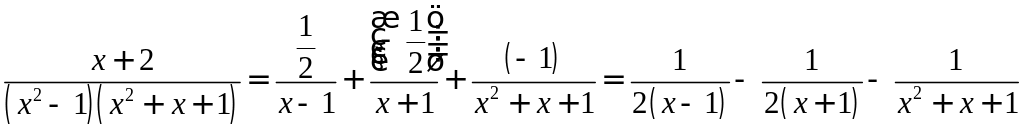
II. Метод произвольных значений
В тождестве (3) переменной х придают n произвольных значений и получают n уравнений с n неизвестными c1, …, cn. В качестве значений х удобно брать значения, равные действительным корням.
Пример.
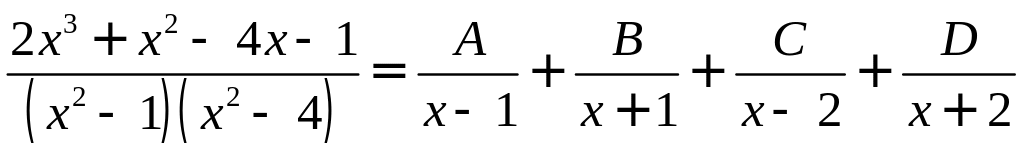 .
.

![]()

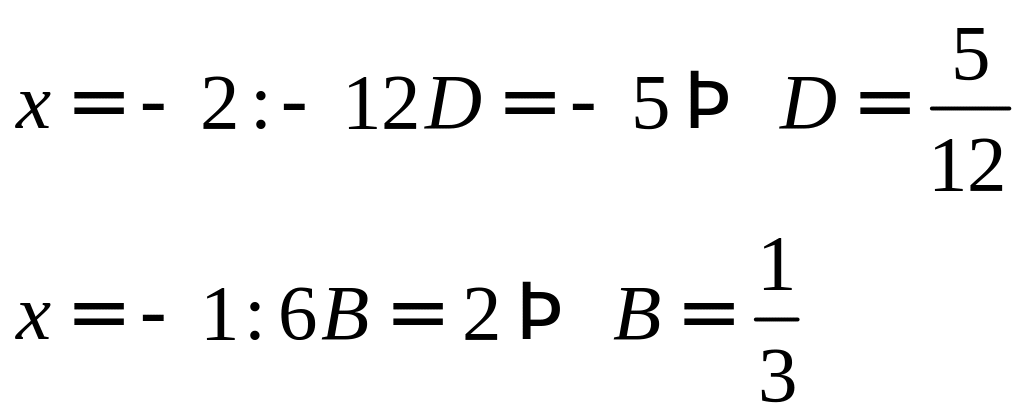
Тогда
 .
.
