Интегральное исчисление функций одной переменной

I. Неопределенный интеграл

§1. Первообразная

Пусть f определена на (а;b), а, b .

Определение 1. Функция F называется первообразной функцией (или первообразной) для функции f на (а;b), если F дифференцируема на (а;b) и F'(x)=f(x).

Если f определена на [а;b], то F имеет производные F'(а+0)=f(а+0), F'(b–0)=f(b-0).

Примеры.

1) Пусть s=s(t) – закон прямолинейного движения материальной точки. Тогда s(t) – первообразная для скорости v(t), т.к. s'(t)=v(t).

Скорость v(t) – первообразная для ускорения a(t), т.к. v'(t)=a(t).

2) F(x)= является первообразной для f(x)=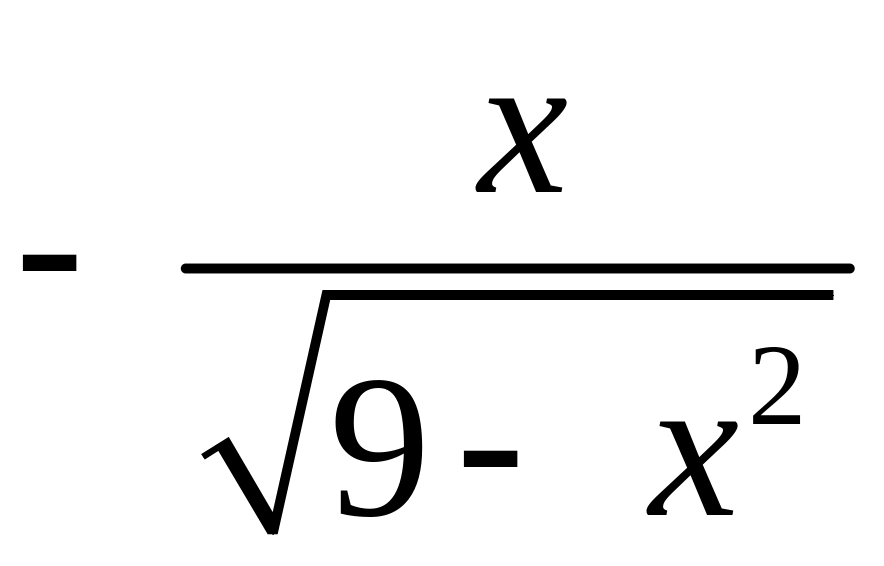 на (-3;3), т.к. F'(x) = x (-3;3).

Теорема 1. Если функция F(x) является первообразной для f(x) на (а;b), то функция F(x)+C (где ) также является первообразной для f(x) на (а;b).

Доказательство.

F'(x)= f(x) x (а;b) (по условию). Рассмотрим функцию F(x)+C. Она дифференцируема на (а;b) и (F(x)+C)'=F'(x)+C' = f(x), т.е. F(x)+C – первообразная для функции f(x) на (а;b).

Теорема 2. Если F₁(x) и F₂(x) – две первообразные для функции f(x) на (а;b), то x (а;b) F₁(x)–F₂(x)=C, С .

Доказательство.

Положим Ф(x)=F₁(x)–F₂(x). Т.к. F₁ и F₂ дифференцируемы на (а;b), то Ф(x) дифференцируема на (а;b).

Ф'(x)=(F₁(x)–F₂(x))=F₁(x)–F₂(x)=f(x)–f(x)=0 x (а;b).

Следовательно, Ф(x)=const, т.е. Ф(x)=C x (а;b). Значит, F₁(x)–F₂(x)=C.

Следствие. Если F(x) является первообразной для f(x) на (а;b), то совокупность всех первообразных для f(x) на (а;b) совпадает с множеством F(x)+C, С .

Определение 2. Множество всех первообразных для функции f(x) на (а;b) называется неопределённым интегралом от функции f на интервале (а;b) и обозначается .

∫ - знак интеграла, f(x)dx – подынтегральное выражение, f(x) – подынтегральная функция.

Согласно определению, если F(x) - одна из первообразных функции f(x) на (а;b), то

=F(x)+C, С (1)

С – постоянная интегрирования.

Равенство (1) – равенство между двумя множествами. Операция нахождения первообразной или неопределённого интеграла от функции f называется интегрированием функции f. Интегрирование – действие, обратное дифференцированию. Следовательно, для проверки правильности интегрирования нужно продифференцировать результат интегрирования.

Важно: если операция дифференцирования однозначна, то операция интегрирования возможна лишь с точностью до постоянного слагаемого.

Возникает вопрос: в каких случаях существует первообразная? Всегда ли можно интегрировать?

Теорема 3. Если f(x) непрерывна на [а;b], то она имеет на нём первообразную, а следовательно и неопределённый интеграл. (Докажем позже)

Если f(x) разрывна на [а;b], то будем рассматривать f(x) только на промежутках непрерывности. На каждом из них она будет интегрируема.

Пример.

f(x)= , x=0 – точка разрыва, (-∞;0) и (0; +∞) – промежутки непрерывности.

На (0;+∞) одной из первообразных является lnx, т.к. (lnx)'= . Тогда , x (0;+∞). На (-∞;0) эта формула лишена смысла, т.к. lnx не определён при x<0. Но на (-∞; 0) одной из первообразных является ln(-x), т.к. (ln(-x))'=  , x (-∞; 0). Таким образом,

Или , x ≠0.

Геометрический смысл неопределённого интеграла

Пусть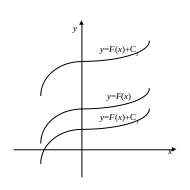 =F(x)+C, x <a;b>. График функции F(x) называется интегральной кривой. Интегральная кривая в каждой точке < а;b> имеет касательную, угловой коэффициент которой равен f(x), (т.к. F'(x)=f(x)). Неопределённый интеграл F(x)+C есть семейство интегральных кривых. Графики любых двух кривых получаются один из другого сдвигом на постоянную величину вдоль оси Оy.