
- •Введение
- •I. Методические указания к ответам на теоретические вопросы
- •§1. Этапы научного исследования. Роль и место вычислительного эксперимента и численных методов
- •§2. Основные понятия теории погрешностей. Общая формула вычисления погрешности
- •§3. Метод Ньютона решения алгебраических и трансцендентных уравнений
- •§4. Решение систем линейных алгебраических уравнений.
- •§5. Метод Гаусса решения систем линейных алгебраических уравнений и его модификации
- •§6. Метод простой итерации решения систем линейных алгебраических уравнений
- •§7. Алгебраическое интерполирование. Исследование существования и единственности интерполяционного полинома
- •§8. Интерполяционный полином Лагранжа.
- •§9. Численное интерполирование. Полином Ньютона
- •§10. Численное интегрирование. Формулы Ньютона-Котеса. Оценка погрешности квадратурных формул
- •§11. Классификация и общая характеристика методов решения дифференциальных уравнений. Хорошо и плохо обусловленные задачи
- •§12. Метод Эйлера. Алгоритм и оценка погрешности
- •§13. Метод Рунге-Кутта. Алгоритм и оценка погрешности
- •§14. Численные методы решения краевых задач для обыкновенных дифференциальных уравнений
- •§15. Идея метода сеток решения уравнений в частных производных
- •§16. Аппроксимация дифференциального уравнения разностным и ее порядок. Устойчивость. Сходимость
- •§17. Метод сеток решения краевых задач для дифференциальных уравнений эллиптического типа
- •II. Методические указания к решению задач
- •Список рекомендуемой литературы
§12. Метод Эйлера. Алгоритм и оценка погрешности
При изложении ответа на этот вопрос следует дать постановку задачи Коши для обыкновенного дифференциального уравнения первого порядка при численном решении, получить вычислительную схему метода Эйлера и его геометрическую интерпретацию, дать оценку погрешности и показать, что задачу Коши для уравнения любого порядка можно свести к задаче Коши для системы дифференциальных уравнений первого порядка, а алгоритмы решения систем получаются из алгоритма решения одного уравнения формальной заменой скалярных величин на векторные.
Пусть дано дифференциальное уравнение
![]() .
(26)
.
(26)
Функция
![]() задана и непрерывна в некоторой области
D
вещественной плоскости. В области D
требуется
найти решение
дифференциального уравнения (26),
проходящее через заданную начальную
точку
задана и непрерывна в некоторой области
D
вещественной плоскости. В области D
требуется
найти решение
дифференциального уравнения (26),
проходящее через заданную начальную
точку
![]() (27)
(27)
При
численном решении уравнения (26)-(27) задача
ставится так: в точках
![]() нужно найти приближения
нужно найти приближения
![]() для значений точного решения
для значений точного решения
![]() уравнения (26) при начальном условии
(27). Разность
уравнения (26) при начальном условии
(27). Разность
![]() называется шагом сетки. Во многих случаях
можно считать, что h>0
– постоянная, не зависящая от номера
n.
называется шагом сетки. Во многих случаях
можно считать, что h>0
– постоянная, не зависящая от номера
n.
Многие приближенные методы опираются на уравнение
 ,
(28)
,
(28)
которое
получается интегрированием уравнения
(26) на отрезке
![]() ;
при этом интеграл в правой части (28)
заменяется тем или иным приближенным
выражением. В методе
Эйлера он
заменяется простейшим образом –
произведением значения подынтегральной
функции на шаг h
(по формуле
левых прямоугольников):
;
при этом интеграл в правой части (28)
заменяется тем или иным приближенным
выражением. В методе
Эйлера он
заменяется простейшим образом –
произведением значения подынтегральной
функции на шаг h
(по формуле
левых прямоугольников):
![]() ,
(29)
,
(29)
Для оценки погрешности метода Эйлера предположим, что 1) функция в области D ограничена
![]() ,
(31)
,
(31)
2)
удовлетворяет условию Липшица по
переменной y,
т.е. существует такая постоянная K,
что для любой пары точек с координатами
![]() и
и
![]() ,
лежащих в области D,
имеет место неравенство
,
лежащих в области D,
имеет место неравенство
![]() .
(32)
.
(32)
3) функция в области D имеет ограниченную производную
![]() .
(33)
.
(33)
Назовем
абсолютной погрешностью приближенного
решения yn
величину
![]() .
Тогда можно показать, что для абсолютной
погрешности
.
Тогда можно показать, что для абсолютной
погрешности
![]() имеет место следующая оценка
имеет место следующая оценка
![]() .
(34)
.
(34)
Таким
образом, при
![]() и выполнении условий (31)-(33) приближенное
решение сходится к точному равномерно
(в области D)
с первым порядком точности.
и выполнении условий (31)-(33) приближенное
решение сходится к точному равномерно
(в области D)
с первым порядком точности.
§13. Метод Рунге-Кутта. Алгоритм и оценка погрешности
При изложении ответа следует дать определение s-стадийного метода Рунге-Кутта, его порядка, записать алгоритм классического метода Рунге-Кутта и применить принцип Рунге для оценки его погрешности.
Рассмотрим метод Рунге-Кутта на примере задачи Коши для обыкновенного дифференциального уравнения первого порядка.
Пусть дана задача
(26)-(27). Требуется определить приближенные
значения y
в точке
![]() ,
где h
–шаг сетки.
,
где h
–шаг сетки.
Определение
1. Пусть s
– положительное целое число (число
стадий или этапов) и
![]() - вещественные коэффициенты. Тогда для
задачи (26)-(27) метод
- вещественные коэффициенты. Тогда для
задачи (26)-(27) метод
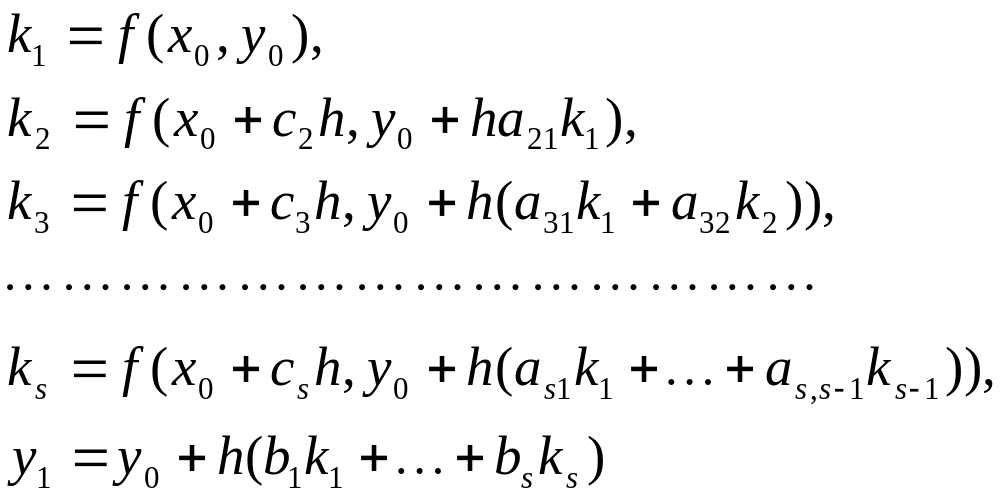 (35)
(35)
называется s-стадийным (s-этапным) явным методом Рунге-Кутта.
Метод Рунге-Кутта позволяет строить схемы различного порядка точности. Эти схемы очень удобны для программирования. В настоящее время они являются наиболее употребительными в практических вычислениях.
Определение 2. Метод Рунге-Кутта (35) имеет порядок p, если для достаточно гладких задач (26)-(27)
![]()
Рассмотрим
в качестве примера без вывода 4-стадийный
метод, имеющий порядок p=4,
называемый классическим методом
Рунге-Кутта. Выберем шаг h
и введем обозначения:
![]() и
и
![]() .
Тогда классический метод Рунге-Кутта
имеет вид
.
Тогда классический метод Рунге-Кутта
имеет вид
![]()

Эффективная оценка погрешности метода Рунге-Кутта затруднительна. Если число p определено, то для грубой оценки погрешности метода можно использовать так называемый принцип Рунге или метод двойного счета.
Пусть
известно, что на каждом шаге допущена
погрешность, приблизительно пропорциональная
![]() (
(![]() ),
и 2m
представляет собой общее число шагов
вычисления. В таком случае, предполагая,
что погрешность на каждом шаге одна и
та же, приближенно получим
),
и 2m
представляет собой общее число шагов
вычисления. В таком случае, предполагая,
что погрешность на каждом шаге одна и
та же, приближенно получим
![]() ,
(36)
,
(36)
где
![]() - значение точного, а
- значение точного, а
![]() - приближенного решения в точке
- приближенного решения в точке
![]() ,
A
– неизвестный числовой множитель.
,
A
– неизвестный числовой множитель.
Согласно Рунге, производим тем же методом вторичный пересчет искомого решения y с двойным шагом H=2h. Тогда в силу нашего предположения будет допущена погрешность
![]() (37)
(37)
где
![]() - значение искомой функции в точке
- значение искомой функции в точке
![]() ,
вычисленное с шагом H=2h.
,
вычисленное с шагом H=2h.
Из
формул (36) и (37) получаем
![]() .
Отсюда находим неизвестную постоянную
.
Отсюда находим неизвестную постоянную
![]()
и, следовательно,
![]()
Таким
образом, приближенно можно положить
![]() ,
,
где
![]() - погрешность вычислений приближенного
значения
- погрешность вычислений приближенного
значения
![]() .
.
Применив принцип Рунге для оценки погрешности классического метода Рунге-Кутта с p=4, получим
![]() .
.
Схемы Рунге-Кутта имеют ряд важных достоинств:
Все они имеют хорошую точность.
Они являются явными, т.е. значение yn+1 вычисляется по ранее найденным значениям за определенное число действий по определенным формулам.
Все схемы допускают расчет с переменным шагом; значит, нетрудно уменьшить шаг там, где функция быстро меняется.
Все схемы являются одношаговыми: для начала расчета достаточно выбрать сетку {
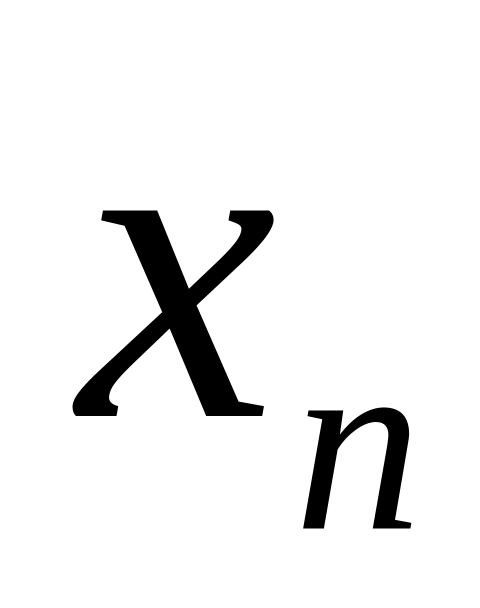 }
и задать значение
}
и задать значение
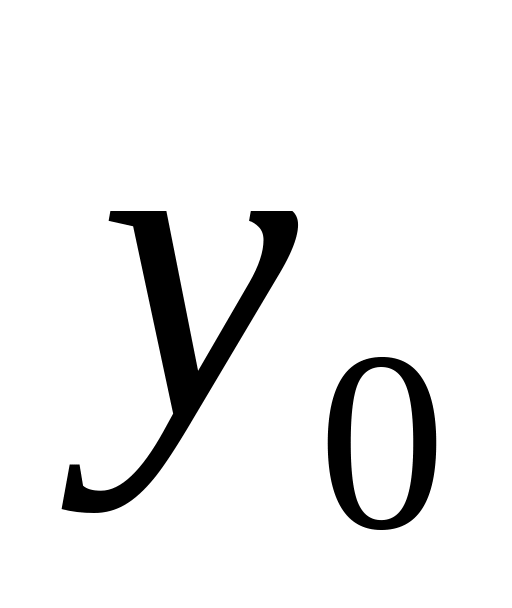 ;
далее вычисления идут по одним и тем
же формулам.
;
далее вычисления идут по одним и тем
же формулам.
