§8. Интерполяционный полином Лагранжа.

Оценка остаточного члена

При изложении ответа на этот вопрос следует дать математическую постановку задачи интерполяции (см §7), получить интерполяционный полином Лагранжа, записать его в различных обозначениях и вывести оценку остаточного члена интерполяционного полинома n-ной степени.

Построение интерполяционного полинома путем решения системы (14) не всегда удобно на практике, так как решение системы уравнений может быть связано с определенными трудностями; кроме того, всегда удобнее иметь явные зависимости коэффициентов интерполяционного полинома от исходных данных. Пусть - узлы интерполяции, i=0,1,…,n - заданные значения функции в этих узлах. Искомый полином будем искать его в виде ,где - полиномы n-й степени, удовлетворяющие следующему условию:

(15)

Положим , при этом удовлетворяет второму из условий (7). Коэффициент c_i подберем так, чтобы полином удовлетворял первому из условий (15):

.

Тогда интерполяционный полином Лагранжа принимает вид:

. (16)

Введем обозначение: . Тогда полином Лагранжа можно записать в виде

. (17)

Погрешность интерполяционного полинома . В узлах интерполяции , в остальных точках эта функция отлична от нуля. Для получения формулы оценки погрешности предположим, что функция n+1 раз непрерывно дифференцируема, и рассмотрим функцию

(18)

Эта функция имеет n+1 корень в узлах интерполяции, подберем коэффициент k так, чтобы в некоторой точке функция u(x) имела n+2 корень:

. (19)

Предположим, что точка при некотором i (0<i<n). Тогда функция принимает нулевые значения на концах каждого из (n+1) интервала [ ], [ ],…,[ ],[ ],…,[ ]. Поэтому согласно теореме Ролля первая производная имеет по крайней мере n+1 корень, вторая производная - по крайней мере n корней и, наконец, (n+1)-я производная имеет по крайней мере один корень. Обозначим этот корень через ξ: . Продифференцируем выражение (18) (n+1) раз: и, подставив , получим

Отсюда

(20)

Приравнивая правые части равенств (19) и (20), получим

.

Учитывая, что - произвольная точка, получим окончательно

, где

§9. Численное интерполирование. Полином Ньютона

При изложении ответа на этот вопрос следует дать математическую постановку задачи интерполяции (см §7), ввести понятие конечной разности, получить первую и вторую формы полинома Ньютона, обосновать их применение.

Интерполяционный полином Ньютона применяется в том случае, когда таблица функции задается с постоянным шагом. Пусть - узлы, , - заданные значения ( ). При построении полинома Ньютона используются конечные разности. Конечной разностью первого порядка называется величина , конечной разностью k-го порядка называется величина .

Интерполяционный полином Ньютона будем искать в виде , где a₀, a₁, …, a_n - коэффициенты, которые требуется определить. Используем для этого определение интерполяционного полинома. Так как , то . Далее . Поэтому . Продолжая таким образом, получаем , и полином Ньютона имеет вид

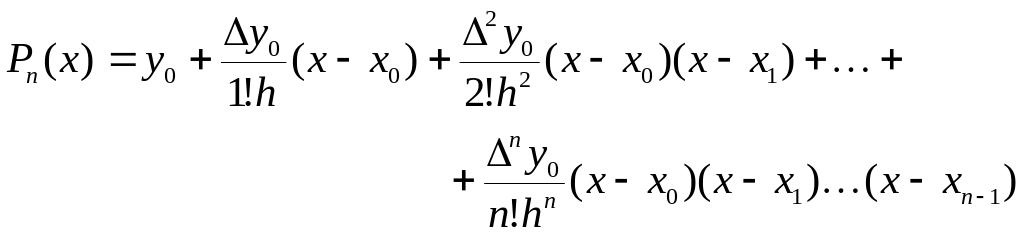(21)

Для некоторых функций f(x) конечные разности с ростом их порядка уменьшаются по абсолютной величине, так что начиная с некоторого номера k, слагаемые в формуле (21) можно не учитывать. В результате уменьшается степень полинома и сокращается объем необходимых вычислений, однако при этом используется не вся заданная таблица. В этом случае применять формулу (21) можно лишь для вычисления значений функции ближе к началу заданной таблицы, т.е. для используемой части таблицы. Для интерполирования вблизи конца таблицы применяется вторая форма полинома Ньютона: