Методы расчёта сводных характеристик выборки Условные варианты

Предположим, что варианты выборки расположены в возрастающем порядке, т.е. в виде вариационного ряда.

Равноотстоящими называются варианты, которые образуют арифметическую прогрессию с разностью .

Условными называются варианты, определяемые равенством

Покажем, что если вариационный ряд состоит из равноотстоящих вариант с шагом то условные варианты есть целые числа. Действительно, выберем в качестве ложного нуля произвольную варианту, например . Тогда , т.к. - целые числа, то их разность 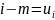- также целое число.

Начальные и центральные теоретические моменты

Начальным теоретическим моментом порядка случайной величины называется математическое ожидание величины и обозначается :

Для непрерывной случайной величины

Центральным теоретическим моментом порядка случайной величины называется математическое ожидание величины и обозначается

Для непрерывной случайной величины

Обычные, начальные и центральные эмпирические моменты

Для вычисления сводных характеристик выборки удобно пользоваться эмпирическими моментами, определения которых аналогичны определениям соответствующих теоретических моментов.

Обычным эмпирическим моментом порядка называется среднее значение k-ых степеней разностей и обозначается :

Начальным эмпирическим моментом порядка называется обычный момент порядка при и обозначается :

Центральным эмпирическим моментом порядка называется обычный момент порядка при и обозначается :

Условные эмпирические моменты

Вычисление центральных моментов требует довольно громоздких вычислений. Чтобы упростить расчёты, заменяют первоначальные варианты условными.

Условным эмпирическим моментом порядка , называется начальный момент порядка , вычисленный для условных вариант:

Выразим обычные моменты через условные: , откуда

Найдя же обычные моменты, можно найти центральные моменты: .

Метод произведений для вычисления выборочных средней и дисперсии

Метод произведений даёт удобный способ вычисления условных моментов различных порядков вариационного ряда с равноотстоящими вариантами. Зная условные моменты, можно найти начальные и центральные эмпирические моменты. Методом произведений удобно вычислять выборочную среднюю и выборочную дисперсию. Покажем применение этого метода на конкретном примере.

Пример 3. Найти методом произведений выборочную среднюю и выборочную дисперсию по заданному распределению выборки объёма

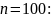
12 14 16 18 20 22

5 15 50 16 10 4

Составим расчётную таблицу