§ 23. Показательное распределение

Определение показательного распределения

1. Опр. Говорят, что непрерывная случайная величина X имеет показательное распределение (экспоненциальное распределение), если

Или

Положительная величина  называется параметром показательного распределения.

Функция распределения

2. Найдем функцию распределения F(x).

Числовые характеристики

3. Найдем числовые характеристики M(X), D(X)

4. Показательное распределение связано с простейшим (стационарным пуассоновским) потоком:

интервал времени T между двумя соседними событиями в простейшем потоке имеет показательное распределение с параметром, равным интенсивности потока

;  – интенсивность потока

§ 24. Моменты распределения.

Опр. Начальным моментом k-го порядка случайной величины X называют математическое ожидание величины X^k.

Для дискретной случайной величины:

Для непрерывной случайной величины:

Частные случаи

1. – начальный момент 1-го порядка это математическое ожидание.

2. 

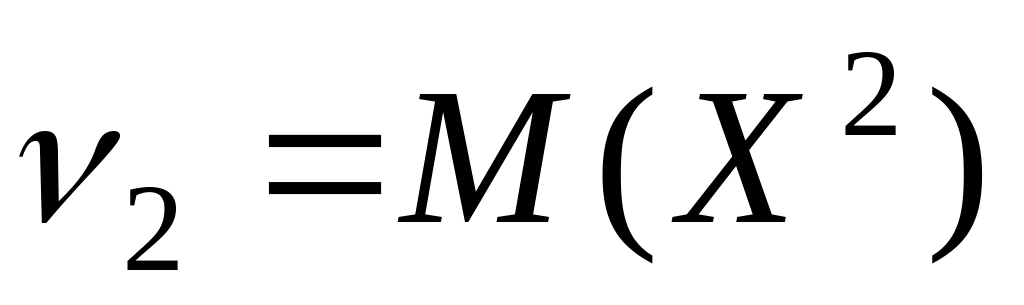
Опр. Центрированной случайной величиной, соответствующей величине X, называется отклонение случайной величины X от ее математического ожидания.

Опр. Центральным моментом k-го порядка случайной величины X называется математическое ожидание k-той степени, соответствующей центрированной случайной величине.

Для дискретной случайной величины:

Для непрерывной случайной величины:

Частные случаи

1. 

2. 

Центральный момент 2-го порядка это дисперсия

*

3. Центральный момент 3-го порядка служит для характеристики асимметрии (или «скошенности») распределения. Если распределение симметрично относительно математического ожидания, то (как и все моменты нечетного порядка), если несимметрично, то

– коэффициент асимметрии

4. Ц

   f(x)

   ентральный момент 4-го порядка служит для характеристики «крутости» (островершинности или плосковершинности) распределения

– эксцесс.

Соотношения, связывающие центральные и начальные моменты

§ 25. Предельные теории вероятностей.

Заранее нельзя сказать какое из возможных значений примет случайная величина в результате испытания. Но при некоторых, достаточно широких условиях, суммарное поведение достаточно большого числа случайных величин почти утрачивает случайный характер и становится закономерным. Эти условия указываются в теоремах, носящих общее название закон больших чисел.

Закон больших чисел играет важную роль в практических применениях. Свойство случайных величин при определенных условиях вести себя практически как неслучайные позволяет оперировать с этими величинами, предсказывать результаты массовых случайных явлений с полной определенностью.

Другая группа теорем, касающихся уже не предельных значений случайных величин, а предельных законов распределения, носят название «центральной предельной теоремы».

Различные формы закона больших чисел + различные формы центральной предельной теоремы образуют совокупность предельных теорем теории вероятностей.