
- •Раздел 3. Динамика (примеры).
- •Тема 1.3 Две основные задачи динамики для материальной точки и их решение
- •Тема 2.4. Геометрия масс. Центр масс механической системы
- •Тема 2.7. Теорема Гюйгенса-Штейнера.
- •Тема 3.7. Теорема о движении центра масс системы
- •Тема 4.3 Импульс силы
- •Тема 4.4 Теорема об изменении количества движения материальной точки
- •Тема 4.5 Теорема об изменении главного вектора количества движения механической системы
- •Тема 4.9 Теорема об изменении кинетического момента механической системы относительно центра и оси
- •Тема 4.11 Работа и мощность сил
- •Тема 4.12 Кинетическая энергия материальной точки и механической системы. Теорема Кенига
- •Тема 4.14 Теорема об изменении кинетической энергии материальной точки
- •Тема 4.16 Потенциальное силовое поле и потенциальная энергия
- •Тема 4.17 . Закон сохранения механической энергии материальной точки и механической системы
Тема 4.12 Кинетическая энергия материальной точки и механической системы. Теорема Кенига
Пример 20.
В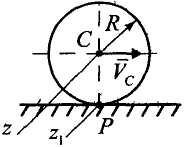 ычислить
кинетическую энергию однородного
диска массы
ычислить
кинетическую энергию однородного
диска массы
![]() ,
катящегося
без скольжения со скоростью
,
катящегося
без скольжения со скоростью
![]() .
.
Решение. Диск совершает плоскопараллельное движение (рис. 20).
1
Рисунок 20
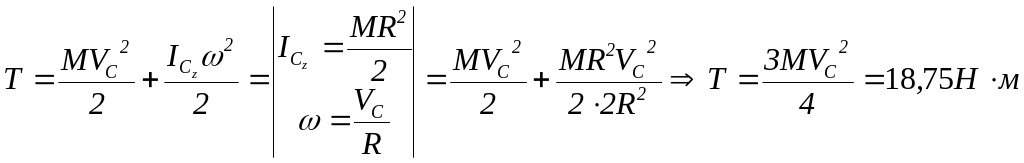
2)
По формуле (4.63)
![]() .
.
Ответ.
![]()
Тема 4.14 Теорема об изменении кинетической энергии материальной точки
Пример 21.
Т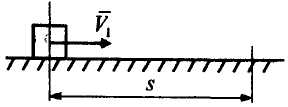
 яжелое
тело поместили на горизонтальную
шероховатую плоскость с коэффициентом
трения
яжелое
тело поместили на горизонтальную
шероховатую плоскость с коэффициентом
трения
![]() и сообщили скорость
и сообщили скорость
![]() .
Какое расстояние до остановки пройдет
тело (рис. 21, а)?
.
Какое расстояние до остановки пройдет
тело (рис. 21, а)?
Решение. Применим теорему в интегральной форме:
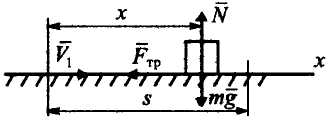
Рисунок 21, а,б![]()
![]() .
Работу совершает только сила трения,
.
Работу совершает только сила трения,
![]() (рис. 21, б).
(рис. 21, б).
![]() .
.
Ответ.
![]()
Пример 22.
К
Рисунок 22, а
![]() и радиуса
и радиуса
![]() .
Масса барабана
.
Масса барабана
![]() распределена
по его ободу радиуса
распределена
по его ободу радиуса
![]() .
К барабану приложен вращающий момент
.
К барабану приложен вращающий момент
![]() .
Пренебрегая скольжением
и трением качения катка по горизонтальной
плоскости и
весом троса (рис. 22, а), определить скорость
катка, когда он переместится на расстояние
.
Пренебрегая скольжением
и трением качения катка по горизонтальной
плоскости и
весом троса (рис. 22, а), определить скорость
катка, когда он переместится на расстояние
![]() .
.
Р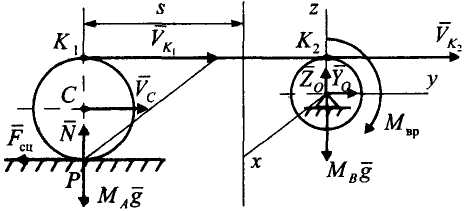 ешение.
Применим
теорему об изменении кинетической
энергии
механической системы в интегральной
форме:
ешение.
Применим
теорему об изменении кинетической
энергии
механической системы в интегральной
форме:
Рисунок 22, б![]()
где
![]() —
система движется из состояния покоя
(рис. 22, б);
—
система движется из состояния покоя
(рис. 22, б);
![]() —
по свойству внутренних сил. Тогда
—
по свойству внутренних сил. Тогда
![]() ,
,
![]() .
Каток
совершает
плоскопараллельное движение.
.
Каток
совершает
плоскопараллельное движение.
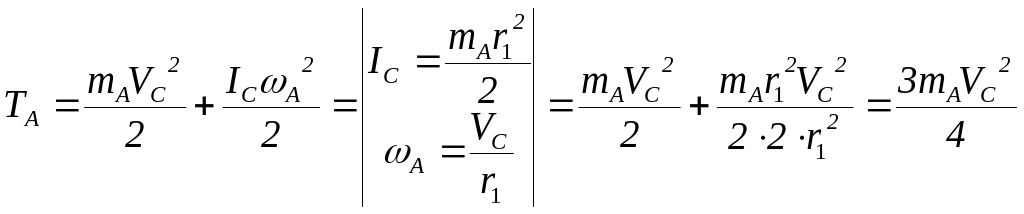
Барабан совершает вращательное движение.
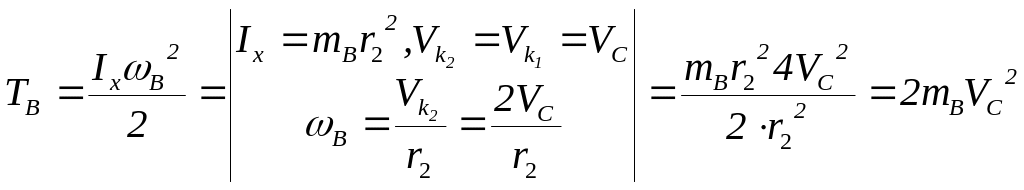 .
.
![]() .
.
Внешними
силами являются силы тяжести
![]() ,
,
![]() и нормальная
реакция
,
сила сцепления
и нормальная
реакция
,
сила сцепления
![]() ,
вращающий
момент
,
вращающий
момент
![]() ,
реакции
,
реакции
![]() и
и
![]() (см.
рис. 22, б).
(см.
рис. 22, б).
![]() ,
т.
к.
,
т.
к.
![]() ;
;
![]() ,
т. к. сила
приложена
в МЦС;
,
т. к. сила
приложена
в МЦС;
![]() A,
т. к.
A,
т. к.
![]() ;
;
![]() ,
,
![]() ,
,
![]() — точка приложения сил не перемещается.
— точка приложения сил не перемещается.
![]() ,
где
,
где
![]() .
Тогда
.
Тогда
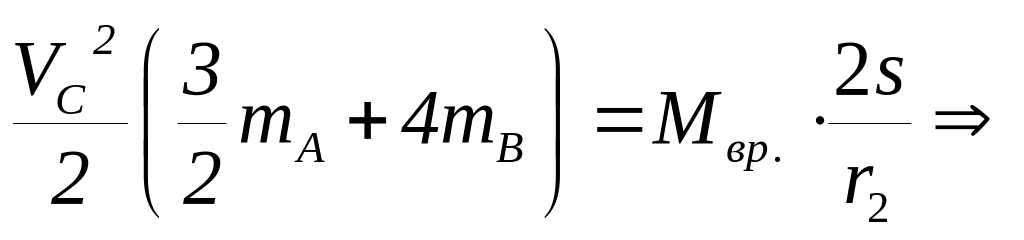
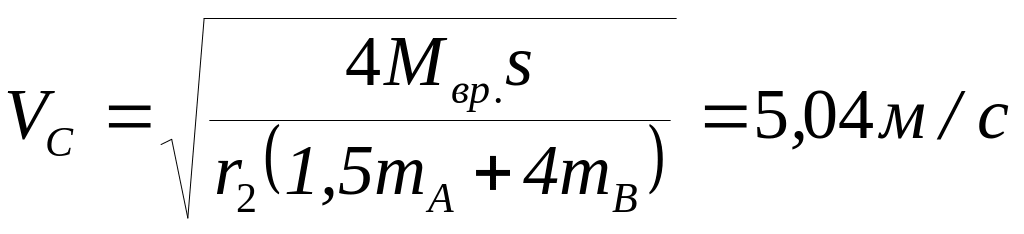 .
.
Ответ.
![]() .
.
Тема 4.16 Потенциальное силовое поле и потенциальная энергия
Пример 23.
Г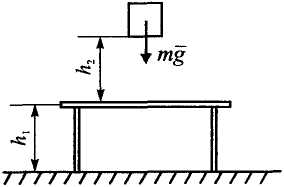 руз
массы
руз
массы
![]() находится
на высоте
находится
на высоте
![]() от стола. Высота
стола
от стола. Высота
стола
![]() .
Определить потенциальную энергию груза
по отношению к столу и по отношению
к полу, принимая их за
нулевой уровень.
.
Определить потенциальную энергию груза
по отношению к столу и по отношению
к полу, принимая их за
нулевой уровень.
Р
Рисунок 23![]() .
По отношению
к полу
.
По отношению
к полу
![]() .
.
Пример 24.
Н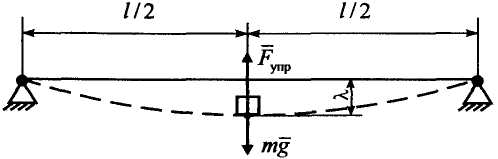 а
середину упругой балки жесткости
а
середину упругой балки жесткости
![]() ,
закрепленной
по концам, положили груз массы
,
закрепленной
по концам, положили груз массы
![]() ,
под действием
которого балка прогнулась на величину
,
под действием
которого балка прогнулась на величину
![]() .
Определить
потенциальную энергию консервативной
системы.
.
Определить
потенциальную энергию консервативной
системы.
Решение. Примем за нулевой уровень ось балки до деформации (рис. 24).
Рисунок 24![]()
Тема 4.17 . Закон сохранения механической энергии материальной точки и механической системы
Пример 25.
Ш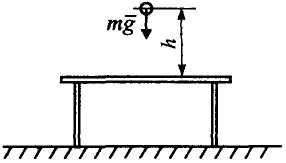 арик
падает на стол с высоты
арик
падает на стол с высоты
![]() без начальной скорости.
Определить скорость шарика в момент
достижения стола.
без начальной скорости.
Определить скорость шарика в момент
достижения стола.
Решение. Примем уровень стола за нулевой. Механическая энергия шарика в начальном положении (рис. 25)
Рисунок 25![]()
![]() .
То же по достижении
стола
.
То же по достижении
стола
![]() ,
т.к.
,
т.к.
![]() .
Тогда
.
Тогда
![]() .
.
Ответ.
![]()
