Тема 4.5 Теорема об изменении главного вектора количества движения механической системы

П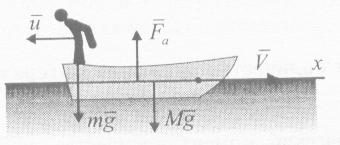 ример 13.

Л

Рисунок 13

одка массы , на корме которой стоял человек массы , двигалась со скоростью . Затем человек спрыгнул с лодки со скоростью против ее движения. С какой скоростью после этого будет двигаться лодка?

Решение. Внешними силами являются вес лодки , вес человека и выталкивающая сила , (рис. 13). Силой сопротивления движению пренебрегаем. Все силы перпендикулярны оси . Поэтому

.

.

Ответ.

Пример 14.

К

Рисунок14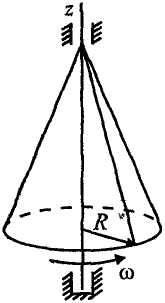

руговой конус вращается вокруг вертикальной оси с угловой скоростью . По образующей конуса движется с вершины конуса материальная точка массы со скоростью . Определить момент количества движения точки относительно оси, когда она находится на расстоянии от вершины, равном половине длины образующей. Радиус основания конуса — (рис. 14).

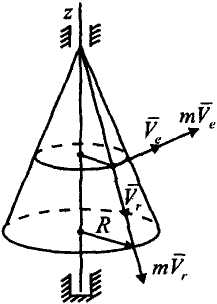
Решение. Точка участвует в сложном движении: в относительном — движении по конусу и в переносном — вращении конуса. Относительная скорость , переносная скорость — . Момент количества движения точки относительно оси . Вектор пересекает ось , поэтому его момент равен нулю, т.е. . Тогда .

Ответ. .

Пример 15.

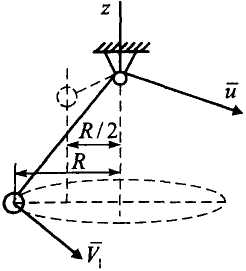
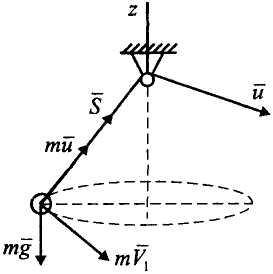К концу нити привязана тяжелая гирька. Второй конец нити переброшен через неп одвижный блок. Когда нить с грузом отклонили от вертикали на некоторый угол и сообщили ему вокруг вертикальной оси скорость , направленную по касательной к траектории, нить начали укорачивать со скоростью . О

Рисунок 15

пределить, с какой скоростью будет двигаться гирька вокруг оси , когда расстояние до оси уменьшится в 2 раза (рис. 15, а).

Решение. На гирьку (рис. 15, б) действуют силы: натяжение нити и вес гирьки. Применим теорему об изменении момента количества движения материальной точки относительно оси : . Сила пересекает ось , параллельна этой оси, поэтому . Вектор пересекает ось , его момент относительно оси равен нулю. Тогда .

Ответ. .

Тема 4.9 Теорема об изменении кинетического момента механической системы относительно центра и оси

Пример 16.

Используя условие примера 14, определить угловую скорость вращения конуса в момент, когда материальная точка будет находиться на основании конуса, если в начальный момент она находилась в вершине конуса, а его угловая скорость . Масса точки , масса конуса .

Решение. Внешними силами, действующими на механическую систему (конус + материальная точка), являются силы тяжести конуса и точки, реакции подпятника — , , и подшипника — и (рис.16). Применим теорему об изменении кинетического момента относительно оси : . Так как внешние силы либо параллельны оси , либо пересекают ее, то ,

т. е. . — кинетический момент конуса. . Тогда .

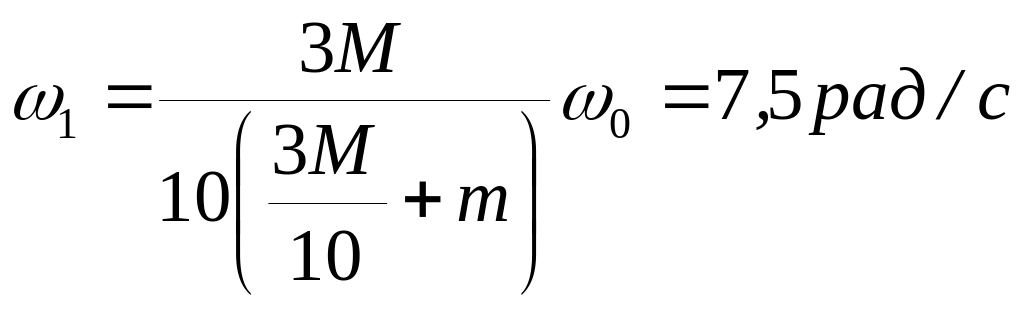О

Рисунок 16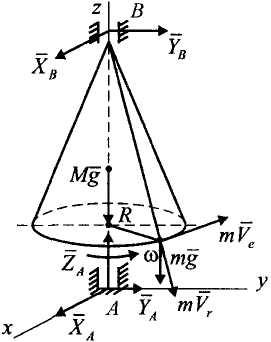

твет. .

Тема 4.11 Работа и мощность сил

Пример 17.

Т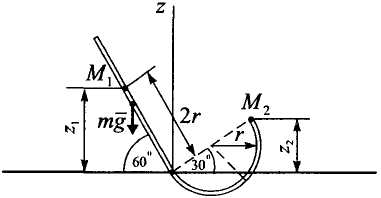 яжелый шарик массы переместился из положения в положение внутри трубки, расположенной в вертикальной плоскости.

О

Рисунок 17

пределить работу силы тяжести шарика на этом перемещении, если (рис. 17).

Решение:

. Ответ.

П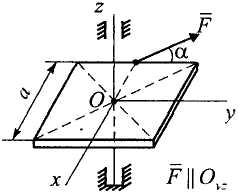 ример 18.

К

Рисунок 18

вадратная пластина со стороной вращается вокруг вертикальной оси под действием силы , образующей с плоскостью пластины угол . Определить работу этой силы, если тело совершило 10 оборотов вокруг оси, a (рис. 18).

Решение.

.

Ответ.

Пример 19.

Определить мощность двигателя для привода механизма подъема груза массы на высоту , если КПД передачи , а груз в течение одной минуты нужно поднять раз.

Решение. Мощность ; . Полезная работа затрачивается на подъем груза (работа силы тяжести) . Тогда . Ответ. .