Раздел 3. Динамика (примеры).

Тема 1.3 Две основные задачи динамики для материальной точки и их решение

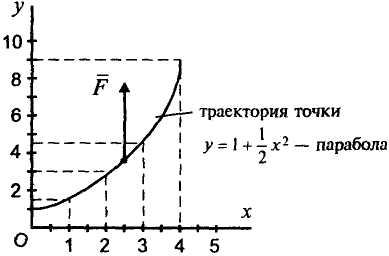П ример 1.

Материальная точка массы движется в плоскости согласно уравнениям ; (рис. 1). Определить силу, действующую на точку.

Р

Рисунок 1

ешение. Проекции силы на оси координат , т. к. . , т. к. .

Ответ: сила, действующая на точку, и направлена параллельно оси .

Пример 2.

Автомобиль массы движется по выпуклому мосту со скоростью . Радиус кривизны в середине моста . Определить силу давления автомобиля на мост в момент, когда он находится на середине моста.

Р

Рисунок 1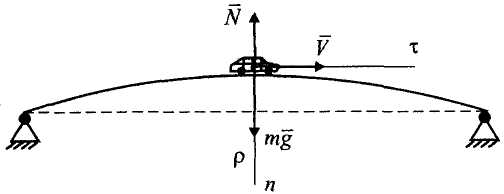

ешение. Считая автомобиль материальной точкой, изобразим его в середине моста и покажем силы: вес и нормальную реакцию (рис. 1). Второй закон динамики в векторной форме . Спроектируем это равенство на естественные оси и :

, .

Давление на мост равно по модулю реакции и направлено в противоположную сторону.

П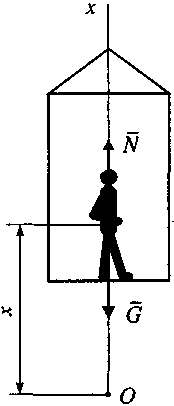 ример 3.

В кабине лифта, движущегося вверх равноускоренно без начальной скорости, стоит человек массы . Определить давление человека на пол кабины, если за время кабина поднялась на высоту .

Решение. Объект движения — человек. Ось направим в сторону движения. На человека действует реакция пола и его вес (рис. 3).

З

Рисунок 3

апишем второй закон динамики в векторной форме и затем в проекции на ось . . Проекция ускорения на ось с учетом (1.10) . Реакция пола .

Давление человека на пол равно реакции и направлено в противоположную сторону.

Примечание: При движении лифта вниз ось направляется также вниз. Тогда , т. е. давление в этом случае меньше силы тяжести.

Пример 4.

На наклонную шероховатую плоскость поместили тяжелое тело и сообщили вверх вдоль плоскости начальную скорость . Угол наклона плоскости равен , коэффициент трения скольжения — . Определить: а) закон изменения скорости движения; б) закон движения тела по плоскости; в) время до остановки; г) расстояние, пройденное до остановки.

Р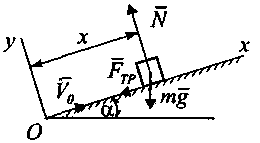 ешение.

1. Выберем начало координат в начальном положении тела, ось направим в сторону движения тела.

2. И

   Рисунок 4

   зобразим тело в произвольном положении на оси , покажем силы, действующие на него: вес , силу трения , и нормальную реакцию плоскости (рис. 4).

3. Запишем дифференциальное уравнение движения тела по оси , . . Получим . Проинтегрируем дважды это уравнение:

,

.

Найдем постоянные интегрирования с учетом начальных условий движения: при , . Тогда

, .

Закон изменения скорости . Закон движения . Время до остановки определим из условия при . . Пройденное расстояние до остановки .

Пример 5.

Тело массы движется горизонтально в среде, сила сопротивления которой . В начальный момент телу сообщили начальную скорость . Определить при :

а) закон изменения скорости движения;

б) закон движения тела;

в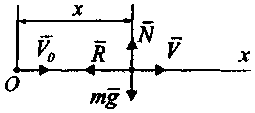 ) время движения, за которое скорость уменьшилась в 2 раза;

г) пройденное за это время расстояние.

Решение.

1

Рисунок 5

. Выберем начало координат в начальном положении тела, ось направим в сторону движения.

2. Покажем в произвольном положении тела силы, действующие на него: вес , силу сопротивления , нормальную реакцию (или выталкивающую силу вязкой среды) (рис. 5).

3. Запишем дифференциальное уравнение движения тела вдоль оси . , т. к. . Обозначим . Тогда

— закон изменения скорости.

Представим . Разделим переменные и проинтегрируем: (взят неопределенный интеграл). Постоянную интегрирования найдем с учетом начальных условий движения: при ,

.

Примечание: Закон движения . Время при .

Примечание: Пройденное за это время расстояние .