Вопрос 32: Движение частиц в потенциальной яме (через потенциальный барьер).

Одномерная прямоугольная «потенциальная яма» с бесконечно высокими «стенками» описывается потенциальной энергией вида

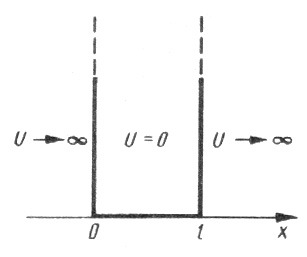
где l – ширина «ямы», а энергия отсчитывается от ее дна (рис. 63).

Пси-функция частицы зависит только от координаты х, поэтому стационарное уравнение Шредингера имеет вид (105)

Частица за пределы «ямы» не проникает, т. е. в областях х<0 и х>1 ψ(х) = 0, а из условия непрерывности следует, что и на границах «ямы» . (106)

В пределах «ямы» (0 ≤ х ≤ l) уравнение Шредингера (105) сведется к уравнению или , (107)

где (108). Общее решение уравнения (106): ψ(x)=Asinkx + Bcoskx.

Так как, по (106), , то В=0. Тогда ψ(x)=Asinkx. (109)

Условию ψ(l) = Asinkl = 0 удовлетворяет равенство

k = πп/l (n = 1, 2, 3, ...) (110)

[значение n = 0 приводит к тривиальному результату ψ(х) = 0, а отрицательные значения п – к тем же функциям, но с отрицательным знаком, что не дает новых физических решений].

Из выражений (108) и (110) получим, что собственные значения энергии частицы (n = 1, 2, 3, ...), (111)

т. е. спектр энергии частицы является дискретным (или квантованным). Квантованные значения Е_n называют уровнями энергии, а число п, их определяющее, – квантовым числом.

Собственные функции задачи получаются подстановкой (110) в (109): ,

а коэффициент А находится из условия нормировки

,

откуда . Тогда нормированные собственные функции

(n = 1, 2, 3, ...). (112)

Из формулы (111) следует, что существует минимальная, не равная нулю энергия ,

соответствующая основному состоянию частицы. Волновая функция основного состояния .

Наличие отличной от нуля минимальной энергии противоречит классической механике и не противоречит соотношению неопределенностей. В самом деле, частица «зажата» в области, на границах которой , поэтому ее положение известно с неопределенностью . Тогда, согласно соотношению неопределенностей [см. (74)], неопределенность импульса . Таким образом, энергия никогда не может быть равна нулю, поскольку это потребовало бы выполнения условия . Состояние с энергией Е₁ называют основным состоянием, а остальные состояния – возбужденными. Энергии возбужденных состояний равны 4Е₁, 9Е₁, 16Е₁,..., соответственно значениям квантового числа n = 2, 3, 4…

Вопрос 30: Волновая функция.

Однако в общем случае состояние частицы в квантовой механике задается более сложной, вообще говоря комплексной, функцией ψ(r,t), зависящей от координат и времени. Эту функцию называют волновой функцией. В частном случае свободного движения частицы волновая функция переходит в плоскую волну де Бройля.

Вероятность dW нахождения частицы в элементе объема dV в момент времени t, согласно статистической интерпретации ψ - функции,

.

Величина имеет смысл плотности вероятности, т. е. определяет вероятность нахождения частицы в момент времени t в окрестности данной точки пространства. Плотность вероятности – величина, наблюдаемая на опыте, в то время как сама волновая функция, являясь комплексной, наблюдению недоступна. В этом заключается существенное отличие в описании состояний частиц в квантовой и классической механике (в классической механике величины, описывающие состояние частиц, наблюдаемы). Вероятность найти частицу в момент времени t в некотором объеме V, согласно теореме сложения вероятностей

(76)

Проинтегрировав выражение (76) в бесконечных пределах, получим вероятность того, что частица в момент времени t находится где-то в пространстве. Это есть вероятность достоверного события, а ее в теории вероятностей считают равной 1. Поэтому принимают, что

(77)

Условие (77) называют условием нормировки, а функцию ψ – нормированной волновой функцией. Так как волновая функция – объективная характеристика состояния микрочастиц, то она должна удовлетворять ряду ограничений. Она должна быть конечной (вероятность не может быть больше единицы), однозначной (вероятность не может быть неоднозначной величиной) и непрерывной (вероятность не может изменяться скачком). В квантовой механике для волновых функций выполняется принцип суперпозиции состояний: если какая-либо система (частица или их совокупность) может находиться в различных состояниях, описываемых волновыми функциями ψ₁, ψ ₂, …, ψ _n, то она может находиться в состоянии ψ, описываемом линейной комбинацией этих функций: ,

где С_n (n = 1, 2, ...) – произвольные (в общем случае комплексные) числа, при этом квадрат модуля коэффициента С_n т. е. \ С_n\², равен вероятности обнаружить, что система, представленная состоянием ψ, может оказаться в состоянии ψ_n.