Решение

Дано:

λ = 600нм

D = 1.2мм

b = 18см

∆b = ?

В центре дифракционной картины будет наблюдаться тёмное пятно, если в отверстии укладывается чётное число зон Френеля. В двух положениях экрана в центре наблюдаются тёмные пятна, когда число зон Френеля, укладывающихся в отверстии, равно двум последовательным чётным числам (например k₁ = m и k₂ = m –2 ). Здесь необходимо учесть, что при увеличении b размер зон Френеля возрастает и их бут всё меньше и меньше укладываться в отверстии. Радиус зоны Френеля с максимальным номером равен радиусу отверстия. Откуда → . Из выражения можно определить m. → m = 3.3333 → m ≈ 4 → ∆b = 18см.

Ответ: ∆b = 18см.

Пример 5. При освещении дифракционной решетки белым светом спектры второго и третьего порядков отчасти перекрывают друг друга. На какую длину волны в спектре второго порядка накладывается фиолетовая граница (λ = 0.4мкм) спектра третьего порядка?

Р ешение

Дано:

λ₁= 0.4мкм

k₁ = 3

k₂ = 2

λ₂ = ?

Для решётки имеем d·sin φ = k·λ. Дифрагированные лучи перекрываются, если угол дифракции φ у них один и тот же. Поэтому в случае перекрывания лучей справедливо k₁ λ₁.= k₂·λ₂. Откуда

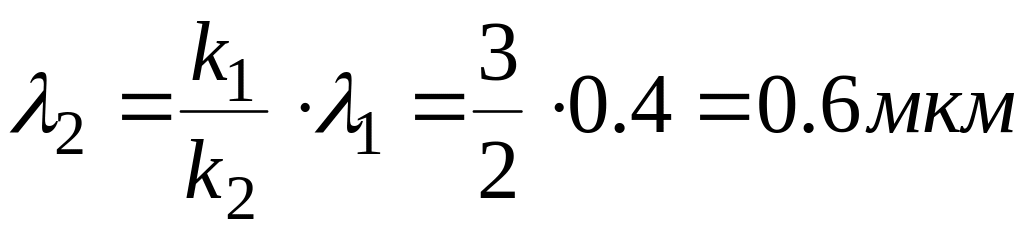
Ответ: λ₂ = 0.6мкм.

Пример 6. Дифракционная картина получена с помощью дифракционной решетки длиной ℓ = 1.5см и периодом d = 5мкм. Определить, в спектре какого наименьшего порядка этой картины получатся раздельные изображения двух спектральных линий с разностью длин волн ∆λ = 0.1нм, если линии лежат в крайней красной части спектра (λ = 760 нм).

Дано: Решение

d = 5мкм

ℓ = 1.5см

λ = 760 нм

∆ λ = 0.1нм

k_min = ?

Согласно критерию Рэлея линии разрешены (видны раздельно), если 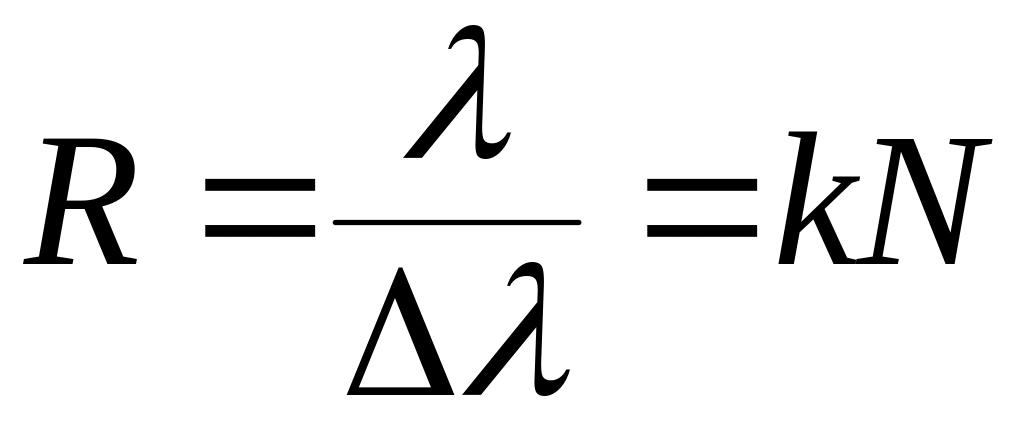где N – общее число штрихов в решётке.

k_min должно быть целым числом. Если величину округлить в меньшую сторону (в данном случае k_min = 2), то формально это означает, что мы передвинулись по спектру ближе к центру, где линии расположены ближе друг к другу и неразрешены. Поэтому округлять всегда надо до ближайшего большего целого числа. Если величина будет целым числом, то в отличие от примера 3. Поэтому в данном случае

Ответ: .

Задачи для самостоятельного решения

2.1. Радиус второго темного кольца Ньютона в отраженном свете r = 0.4мм. Определить радиус R кривизны плосковыпуклой линзы, взятой для опыта, если она освещается монохроматическим светом с длиной волны λ= 0.64мкм.

2.2. Свет от монохроматического источника падает нормально на диаграмму с диаметром отверстия За диафрагмой на расстоянии от нее находится экран. Какое число зон Френеля укладывается в отверстии диаграммы? Каким будет центр дифракционной картины на экране на экране: темным или светлым?

2.3. Найти радиусы первых пяти зон Френеля если расстояние от источника света до волновой поверхности расстояние света до волновой поверхности до точки наблюдения Длина волны света

2.4. Вычислить радиус r₅ пятой зоны Френеля для плоского волнового фронта (к = 0.5мкм), если построение делается для точки наблюдения, находящейся на расстоянии b = lм от фронта волны.

2.5. Радиус r₄ четвертой зоны Френеля для плоского волнового фронта равен 3мм. Определить радиус r₆ шестой зоны Френеля.

2.6. На диафрагму с круглым отверстием диаметром d = 4мм падает нормально параллельный пучок лучей монохроматического света (λ = 0.5мкм). Точка наблюдения находится на оси отверстия на расстоянии b = 1м от него. Сколько зон Френеля укладывается в отверстии? Темное или светлое пятно получится в центре дифракционной картины, если в месте наблюдений поместить экран?

2.7. Плоская световая волна (λ = 0.5мкм) падает нормально на диафрагму с круглым отверстием диаметром d = lсм. На каком расстоянии b от отверстия должна находиться точка наблюдения, чтобы отверстие открывало: 1) одну зону Френеля? 2) две зоны Френеля?

2.8. Плоская световая волна падает нормально на диафрагму с круглым отверстием. В результате дифракции в некоторых точках оси отверстия, находящихся на расстояниях b от его центра, наблюдаются максимумы интенсивности. 1. Получить вид функции b = f(r, λ, n), где r — радиус отверстия; λ, — длина волны; n – число зон Френеля, открываемых для данной точки оси отверстием. 2. Сделать то же самое для точек оси отверстия, в которых наблюдаются минимумы интенсивности.

2.9. Плоская световая волна (λ = 0.7мкм) падает нормально на диафрагму с круглым отверстием радиусом r = 1.4мм. Определить расстояния b_l, b₂, b₃ от диафрагмы до трех наиболее удаленных от нее точек, в которых наблюдаются минимумы интенсивности .

2.10. Точечный источник S света(λ = 0.5мкм), плоская диафрагма с круглым отверстием радиусом r =1мм и экран расположены, как это указано на рис. 31.4 (а = 1м). Определить расстояние b от экрана до диафрагмы, при котором отверстие открывало бы для точки Р три зоны Френеля.

2.11. Как изменится интенсивность в точке Р (см. задачу 31.8), если убрать диафрагму?

2.12. На щель шириной а = 0.05мм падает нормально монохроматический свет (λ = 0.6мкм). Определить угол φ между первоначальным направлением пучка света и направлением на четвертую темную дифракционную полосу.

2.13. На узкую щель падает нормально монохроматический свет. Угол φ отклонения пучков света, соответствующих второй светлой дифракционной полосе, равен 1°. Скольким длинам волн падающего света равна ширина щели?

2.14. На щель шириной а = 0.1мм падает нормально монохроматический свет (λ = 0.5мкм). За щелью помещена собирающая линза, в фокальной плоскости которой находится экран. Что будет наблюдаться на экране, если угол φ дифракции равен: 1) 17'; 2) 43'.

2.15. Сколько штрихов на каждый миллиметр содержит дифракционная решетка, если при наблюдении в монохроматическом свете (λ = 0.6мкм) максимум пятого порядка отклонен на угол φ = 18°?

2.16. На дифракционную решетку, содержащую n = 100 штрихов на 1мм, падает нормально монохроматический свет. Зрительная труба спектрометра наведена на максимум третьего порядка. Чтобы навести трубу на другой максимум того же порядка, ее нужно повернуть на угол ∆φ = 20°. Определить длину волны λ света.

2.17. Дифракционная решетка освещена нормально падающим монохроматическим светом. В дифракционной картине максимум второго порядка отклонен на угол φ₀. На какой угол φ₂ отклонен максимум третьего порядка?

2.18. Дифракционная решетка содержит n = 200 штрихов на 1мм. На решетку падает нормально монохроматический свет (λ = 0.6мкм). Максимум какого наибольшего порядка дает эта решетка?

2.19. На дифракционную решетку, содержащую n = 400 штрихов на 1мм, падает нормально монохроматический свет (λ = 0.6мкм). Найти общее число дифракционных максимумов, которые дает эта решетка. Определить угол φ дифракции, соответствующий последнему максимуму.

2.20. При освещении дифракционной решетки белым светом спектры второго и третьего порядков отчасти перекрывают друг друга. На какую длину волны в спектре второго порядка накладывается фиолетовая граница (λ = 0.4мкм) спектра третьего порядка?

2.21. На дифракционную решетку, содержащую n = 500 штрихов на 1мм, падает в направлении нормали к ее поверхности белый свет. Спектр проецируется помещенной вблизи решетки линзой на экран. Определить ширину b спектра первого порядка на экране, если расстояние L линзы до экрана равно 3м. Границы видимости спектра λ_кр = 780нм, λ_ф = 400нм.

2.22. На дифракционную решетку с периодом d=10мкм под углом а=30° падает монохроматический свет с длиной волны λ = 600нм. Определить угол φ дифракции, соответствующий второму главному максимуму.

2.23. Какой наименьшей разрешающей силой R должна обладать дифракционная решетка, чтобы с ее помощью можно было разрешить две спектральные линии калия (λ₁ =578 нм и λ₂ = 580нм)? Какое наименьшее число N штрихов должна иметь эта решетка, чтобы разрешение было возможно в спектре второго порядка?

2.24. С помощью дифракционной решетки с периодом d = 20мкм требуется разрешить дублет натрия (λ₁ = 589.0нм и λ₂ = 589.6нм) в спектре второго порядка. При какой наименьшей длине ℓ решетки это возможно?

2.25. Угловая дисперсия 1)ф дифракционной решетки для излучения некоторой длины волны (при малых углах дифракции) составляет 5 мин/нм. Определить разрешающую силу R этой решетки для излучения той же длины волны, если длина / решетки равна 2см.

2.26. Определить угловую дисперсию D_φ дифракционной решетки для угла дифракции φ = 30° и длины волны λ = 600нм. Ответ выразить в единицах СИ и в минутах на нанометр.

2.27. На дифракционную решетку, содержащую n = 500 штрихов на 1мм, падает нормально монохроматический свет с длиной волны λ = 700нм. За решеткой помещена собирающая линза с главным фокусным расстоянием f = 50см. В фокальной плоскости линзы расположен экран. Определить линейную дисперсию D_ℓ такой системы для максимума третьего порядка. Ответ выразить в миллиметрах на нанометр.

2.28. Нормально поверхности дифракционной решетки падает пучок света. За решеткой помещена собирающая линза с оптической силой D = 1 дптр. В фокальной плоскости линзы расположен экран. Определить число n штрихов на 1мм этой решетки, если при малых углах дифракции линейная дисперсия D_ℓ = 1 мм/нм.

2.29. На дифракционную решетку нормально ее поверхности падает монохроматический свет (λ = 650нм). За решеткой находится линза, в фокальной плоскости которой расположен экран. На экране наблюдается дифракционная картина под углом дифракции φ = 30°. При каком главном фокусном расстоянии f линзы линейная дисперсия D_ℓ = 0.5мм/нм?

2.30. На грань кристалла каменной соли падает параллельный пучок рентгеновского излучения (λ = 147пм). Определить расстояние d между атомными плоскостями кристалла, если дифракционный максимум второго порядка наблюдается, когда излучение падает под углом θ = 31°30' к поверхности кристалла.

2.31. Какова длина волны λ монохроматического рентгеновского излучения, падающего на кристалл кальцита, если дифракционный максимум первого порядка наблюдается, когда угол θ между направлением падающего излучения и гранью кристалла равен 3°? Расстояние d между атомными плоскостями кристалла принять равным 0.3нм.

2.32. Параллельный пучок рентгеновского излучения падает на грань кристалла. Под углом θ = 65° к плоскости грани наблюдается максимум первого порядка. Расстояние d между атомными плоскостями кристалла 280пм. Определить длину волны λ рентгеновского излучения.