
- •Содержание Введение 4 Указания к выполнению заданий и контрольных работ 5
- •Введение
- •1. Интерференция света
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Р ешение
- •Задачи для самостоятельного решения
- •Дифракция света
- •Примеры решения задач
- •Решение
- •Решение
- •Р ешение
- •Задачи для самостоятельного решения
- •3. Взаимодействие электромагнитных волн с веществом
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •4. Поляризация света Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Ответ : Задачи для самостоятельного решения
- •Решение
- •Решение
- •Р ешение
- •Ответ :
- •Р ешение
- •Задачи для самостоятельного решения
- •6. Теория атома водорода по Бору
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •7. Элементы квантовой механики
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Р z ешение
- •Решение
- •Задачи для самостоятельного решения
- •8. Элементы современной физики атомов и молекул
- •Примеры решения задач
- •Решение
- •Р ешение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •9. Элементы физики твердого тела
- •Примеры решения задач
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •10. Элементы физики атомного ядра
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Индивидуальные задания Тема 1. Интерференция света.
- •Тема 2. Дифракция света.
- •Тема 3. Взаимодействие электромагнитных волн с веществом.
- •Тема 4. Поляризация света.
- •Тема 5. Квантовая природа излучения.
- •Тема 6. Теория атома водорода по Бору.
- •Тема 7. Элементы квантовой механики.
- •Тема 8. Элементы современной физики атомов и молекул.
- •Тема 9. Элементы физики твердого тела.
- •Тема 10. Элементы физики атомного ядра.
- •1.Ответы. Интерференция.
- •2 Ответы. Дифракция.
- •3. Ответы. Взаимодействие света с веществом.
- •4. Ответы. Поляризация.
- •5. Ответы. Тепловое излучение.
- •6. Ответы. Атом Бора.
- •7. Ответы. Элементы квантовой механики.
- •8. Ответы. Элементы современной физики атомов и молекул
- •9. Ответы. Элементы физики твердого тела
- •10. Ответы. Элементы физики атомного ядра
- •Литература
- •Сборник индивидуальных заданий
Примеры решения задач
Пример
1. Ядро
цинка
![]() захватило электрон из К – оболочки и
спустя некоторое время испустило
позитрон. Какое ядро получилось в
результате этих превращений?
захватило электрон из К – оболочки и
спустя некоторое время испустило
позитрон. Какое ядро получилось в
результате этих превращений?
Решение
Запишем уравнения происходящих реакций
![]() второй
этап реакции
второй
этап реакции
![]()
При
решении использовали законы сохранения
массового
и
зарядового
чисел.
![]() для первой реакции и
для первой реакции и
![]() для второй.
для второй.
Ответ:
![]() .
.
Пример 2. Водород обогащён дейтерием. Определить массовые доли ω1 протия и ω2 дейтерия, если относительная атомная масса Аr такого водорода оказалась равной 1.122.
Решение
Массовые
доли ω1
протия и ω2
дейтерия
это:
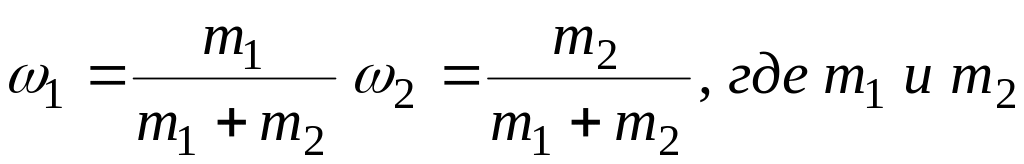 −
массы дейтерия и протия в смеси.
−
массы дейтерия и протия в смеси.
![]() -
протий или водород (ядро - протон);
-
протий или водород (ядро - протон);
![]() -
дейтерий (ядро - один протон плюс один
нейтрон);
-
дейтерий (ядро - один протон плюс один
нейтрон);
Далее
![]() .
По определению молярная масса это
.
По определению молярная масса это
![]() ,
где
,
где
![]() − масса (в данном случае смеси),
− масса (в данном случае смеси),
 − общее количество вещества. Откуда
− общее количество вещества. Откуда
 .
Учитывая, что
.
Учитывая, что
![]() получаем
получаем
 ,
где
,
где
![]() и
и
![]() относительные
атомные массы соответственно протия и
дейтерия. Но
относительные
атомные массы соответственно протия и
дейтерия. Но
![]() .
Учитывая это
окончательно получаем
.
Учитывая это
окончательно получаем

Из
таблицы Менделеева находим
![]() (протий
H)
и
(протий
H)
и
![]() (дейтерий
D)
. Подставив числовые значения в последние
формулы, получаем:
(дейтерий
D)
. Подставив числовые значения в последние
формулы, получаем:
![]()
Ответ:
![]() .
.
Пример 3. При определении периода полураспада изотопа Т½ использован счётчик импульсов. За время ∆t = 1мин в начале наблюдения (t = 0) было насчитано ∆n1= 250 импульсов. По истечении времени t = 1ч насчитано за тот же промежуток времени ∆n2= 92 импульса. Определить период полураспада изотопа Т½ и постоянную распада λ.
Решение
Дано:
∆t = 1мин
∆n1= 250
∆n2= 92
t = 1ч
λ. = ?
Т½ = ?
Ясно,
что число зарегистрированных за время
∆t импульсов ∆n пропорционально числу
распавшихся атомов ∆N. При первом
измерении (t = 0) ∆n1
= k∆N1=kN1(1
− e-∆λt),
где N1-
количество имеющихся в начальный момент
атомов, k
– коэффициент пропорциональности между
числом распавшихся атомов и числом
сосчитанных прибором импульсов (∆n =
k∙∆N)
(постоянная для данного прибора величина).
Аналогично в момент времени t будет ∆n2
= k∆N2=kN2(1
− e-∆λt),
где N2
- количество имеющихся в момент времени
t атомов. Согласно закону радиоактивного
распада N2 = N1e-λt.
Откуда

 Т½
=
Т½
=![]()
Ответ:
![]() ,
Т½
,
Т½
![]() .
.
Пример 4. Активность препарата уменьшилась в k = 250 раз. Скольким периодам полураспада Т½ равен протекший промежуток времени t?
Решение
Дано:
k = 250
t
= ? Активность зависит от времени
по закону
![]() ,
где
,
где
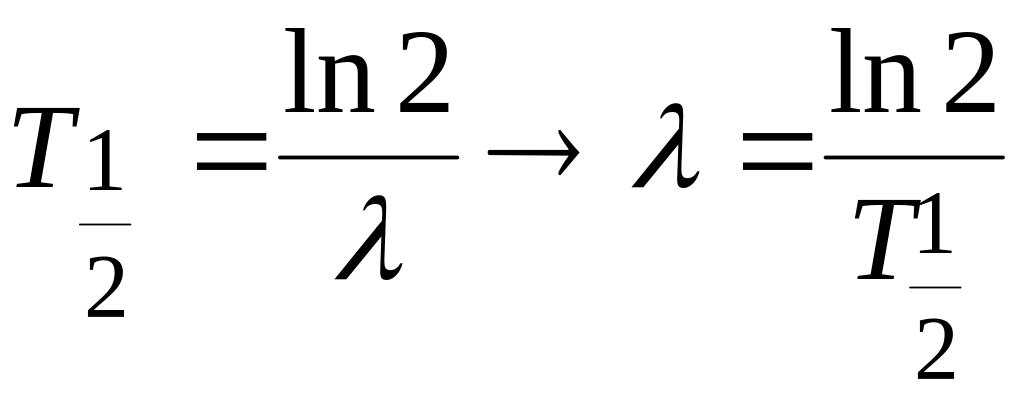 .
Откуда
.
Откуда
 и
и

Ответ: t = 8∙T½.
Пример
5. Определить
удельную энергию связи ядра
![]()
Решение
По
определению
![]() .
Подставляя числовые значения получаем
.
Подставляя числовые значения получаем

Ответ:
![]() .
.
Пример
6. Определить
энергию Е, которую нужно затратить для
отрыва нейтрона от ядра
![]()
![]() .
.
Решение
После
отрыва нейтрона
![]() .
Т.е.
.
Т.е.
![]() .
Число электронов в атомах этих изотопов
(11) одинаково. Откуда
.
Число электронов в атомах этих изотопов
(11) одинаково. Откуда
![]()
Ответ:
![]() .
.
Пример 7. Атомное ядро, поглотившее γ – фотон (λ = 0.47пм), пришло в возбуждённое состояние и распалось на отдельные нуклоны, разлетевшиеся в разные стороны. Суммарная кинетическая энергия Ек нуклонов равна 0.4МэВ. Определить энергию связи Есв ядра. (2.2МэВ)
Решение
Дано:
λ = 0.47пм
Е к
= 0.4МэВ =
к
= 0.4МэВ =
![]() Дж
Дж
Есв= ?
Из
закона сохранения энергии следует, что
![]() .
Отсюда
.
Отсюда

Ответ:
![]() .
.
Пример
8.Определить
массовый расход mt
ядерного горючего
![]() в ядерном реакторе атомной электростанции.
Тепловая мощность Р электростанции
равна 10МВт. Принять энергию Q,
выделяющуюся при одном акте деления,
равной 200МэВ. КПД η станции равен 20℅.
(53г)
в ядерном реакторе атомной электростанции.
Тепловая мощность Р электростанции
равна 10МВт. Принять энергию Q,
выделяющуюся при одном акте деления,
равной 200МэВ. КПД η станции равен 20℅.
(53г)
Решение
Дано:
P = 10МВт
μ = 235г/моль
η = 20℅
Q = 200МэВ
mt = ?
Энергия,
вырабатываемая станцией за время t будет
 ,
но
,
но
![]() .
Отсюда
.
Отсюда
![]() .
.
Ответ:
![]() .
.
Задачи для самостоятельного решения
Определить массу нейтрального атома хрома
 .
.
Объяснить отличие изотопов и изобаров.
Определить, какую часть массы нейтрального атома
 (m = 19.9272.10-27кг)
составляет масса его электронной
оболочки.
(m = 19.9272.10-27кг)
составляет масса его электронной
оболочки.
Определить число протонов и нейтронов, входящих в состав ядер трех изотопов бора: 1)
 ;
2)
;
2) ;
3)
;
3) .
.Определить число протонов и нейтронов, входящих в состав ядер трех изотопов кислорода: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 .
.Определить, пользуясь таблицей Менделеева, число нейтронов и протонов в атомах платины и урана.
Определить зарядовые числа ядер, массовые числа и символы ядер, которые получатся, если в ядрах, нейтроны заменить протонами, а протоны – нейтронами.
Определить плотность ядерного вещества, выражаемую числом нуклонов в 1 см3, если в ядре с массовым числом А все нуклоны плотно упакованы в пределах его радиуса.
Объяснить, почему плотность ядерного вещества примерно одинакова для всех ядер.
Определить, что больше – масса атомного ядра или масса свободных нуклонов (протонов и нейтронов), входящих в его состав.
Определить, какая энергия в электрон-вольтах соответствует дефекту массы Δm = 3·10-20 мг.
Определить энергию связи ядра атома гелия
 .
Масса нейтрального атома гелия равна
6.6467.10-27кг.
.
Масса нейтрального атома гелия равна
6.6467.10-27кг.
Определить удельную энергию связи δЕСВ (энергию связи, отнесенную к одному нуклону) для ядер: 1)
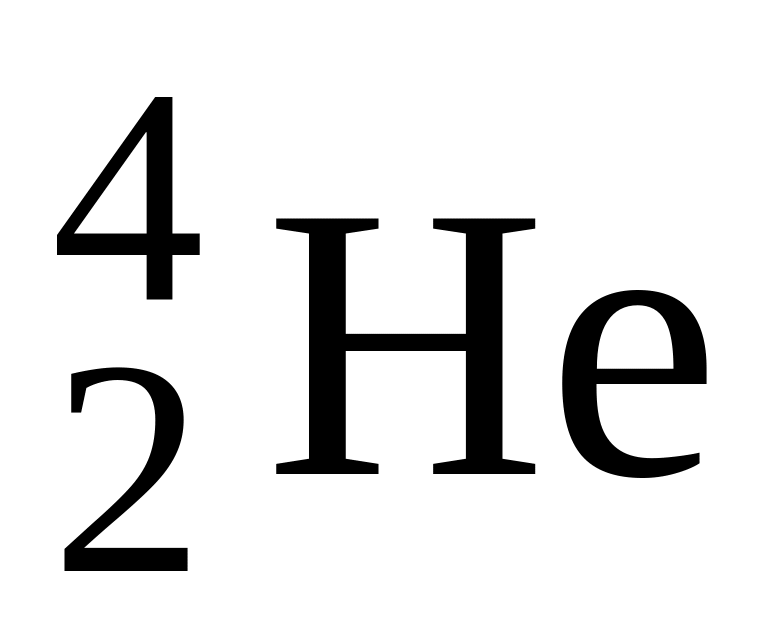 ;
2)
;
2)
 .
Массы нейтральных атомов гелия и
углерода соответственно равны
6.6467.10-27
и 19.9272.10-27кг.
.
Массы нейтральных атомов гелия и
углерода соответственно равны
6.6467.10-27
и 19.9272.10-27кг.
Используя данные задачи 10.13, определить, какая необходима энергия, чтобы разделить ядро
 на три альфа-частицы.
на три альфа-частицы.
Определить массу изотопа
 ,
если изменение массы при образовании
ядра
составляет 0.2508.10-27кг.
,
если изменение массы при образовании
ядра
составляет 0.2508.10-27кг.
При отрыве нейтрона от ядра гелия
 образуется ядро
образуется ядро
 .
Определить энергию, которую необходимо
для этого затратить. Массы нейтральных
атомов
и
соответственно равны 6.6467·40-27
и 5.0084·10-27кг.
.
Определить энергию, которую необходимо
для этого затратить. Массы нейтральных
атомов
и
соответственно равны 6.6467·40-27
и 5.0084·10-27кг.
Энергия связи EСВ ядра, состоящего из трех протонов и четырех нейтронов, равна 39.3 МэВ. Определить массу m нейтрального атома, обладающего этим ядром.
Определить, какую долю кинетической энергии теряет нейтрон при упругом столкновении с покоящимся ядром углерода , если после столкновения частицы движутся вдоль одной прямой. Массу нейтрального атома углерода принять равной 19.9272·10-27кг.
Определить число нуклонов, которые могут находиться в ядре на наинизшем квантовом уровне.
Определить, во сколько раз магнетон Бора (единица магнитного момента электрона) больше ядерного магнетона (единица магнитного момента ядра).
Охарактеризовать свойства и особенности сил, действующих между составляющими ядро нуклонами.
Объяснить принципы построения ядерной и оболочечной моделей ядра.
Объяснить, почему радиоактивные свойства элементов обусловлены только структурой их ядер.
Считая постоянную λ радиоактивного распада известной и используя закон радиоактивного распада, вывести выражение для: 1) периода полураспада Т1/2 радиоактивного ядра; 2) среднего времени жизни τ радиоактивного ядра.
Определить постоянную радиоактивного распада λ для изотопов: 1) тория
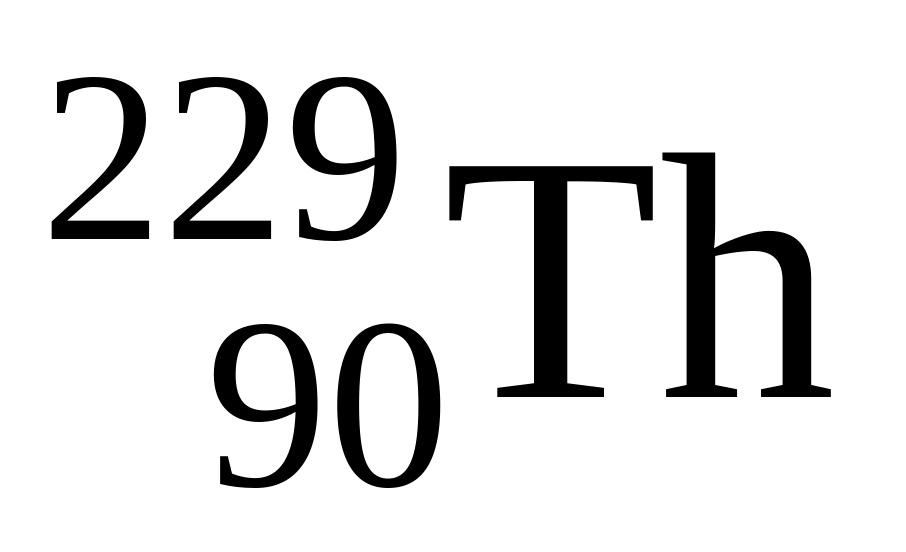 ;
2) урана
;
2) урана
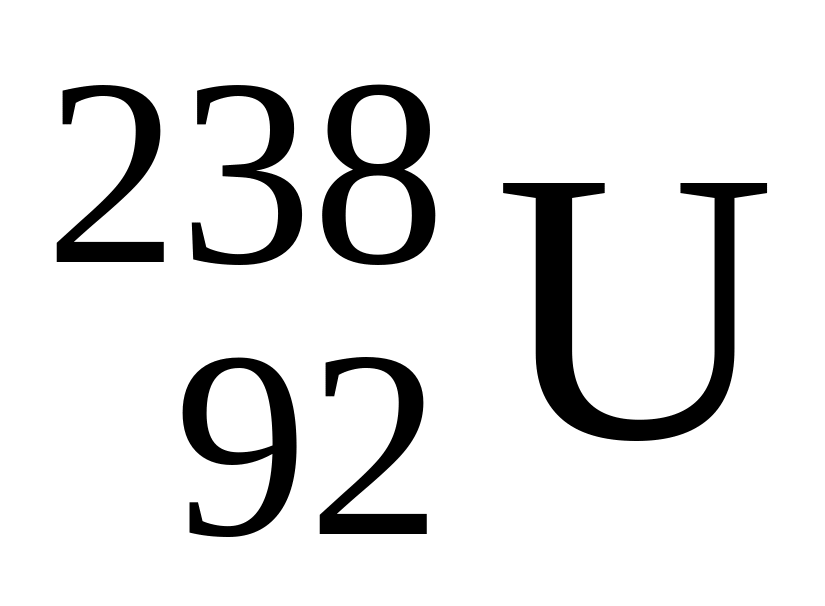 ;
3) иода
;
3) иода
 I.
Периоды полураспада этих изотопов
соответственно равны: 1) 7.103лет;
2) 4.5.109 лет;
3) 8 сут.
I.
Периоды полураспада этих изотопов
соответственно равны: 1) 7.103лет;
2) 4.5.109 лет;
3) 8 сут.
Определить, что (и во сколько раз) продолжительнее – три периода полураспада или два средних времени жизни радиоактивного ядра.
Определить, во сколько раз начальное количество ядер радиоактивного изотопа уменьшится за три года, если за один год оно уменьшилось в 4 раза.
Определить, какая часть (%) начального количества ядер радиоактивного изотопа останется не распавшейся по истечении времени t, равного двум средним временам жизни τ радиоактивного ядра.
Определить, какая часть начального количества ядер радиоактивного изотопа распадется за время t, равное двум периодам полураспада T1/2.
Определить период полураспада радиоактивного изотопа, если 5/8 начального количества ядер этого изотопа распалось за время t = 849 с.
Период полураспада радиоактивного изотопа актиния
 составляет 10 сут. Определить время, за
которое распадется 1/3
начального количества ядер актиния.
составляет 10 сут. Определить время, за
которое распадется 1/3
начального количества ядер актиния.
Постоянная радиоактивного распада изотопа
 равна 10-9
с-1.
Определить время, в течение которого
распадется 2/5
начального количества ядер этого
радиоактивного изотопа.
равна 10-9
с-1.
Определить время, в течение которого
распадется 2/5
начального количества ядер этого
радиоактивного изотопа.
Первоначальная масса радиоактивного изотопа иода
 (период полураспада Т1/2
= 8 сут) равна 1г. Определить: 1) начальную
активность изотопа; 2) его активность
через 3 сут.
(период полураспада Т1/2
= 8 сут) равна 1г. Определить: 1) начальную
активность изотопа; 2) его активность
через 3 сут.
Активность некоторого радиоактивного изотопа в начальный момент времени составляла 100 Бк. Определить активность этого изотопа по истечении промежутка времени, равного половине периода полураспада.
Начальная активность 1г изотопа радия
 равна 1 Ки. Определить период полураспада
T1/2
этого
изотопа.
равна 1 Ки. Определить период полураспада
T1/2
этого
изотопа.
Принимая, что все атомы изотопа магния
 (Т½=10 мин)
массой m
= 1 мкг радиоактивны, определить: 1)
начальную активность А0
этого изотопа; 2) его активность А через
3 сут.
(Т½=10 мин)
массой m
= 1 мкг радиоактивны, определить: 1)
начальную активность А0
этого изотопа; 2) его активность А через
3 сут.
Определить период полураспада T1/2 некоторого радиоактивного изотопа, если его активность за 5 сут уменьшилась в 2.2 раза.
Определить удельную активность а (число распадов в 1 с на 1кг вещества) изотопа , если период его полураспада T1/2 = 4.5·109 лет.
Объяснить, как изменяется положение химического элемента в таблице Менделеева после α- и β-распадов ядер его атомов.
Пользуясь таблицей Менделеева и правилами смещения, определить, в какой элемент превращается после трех α- и двух β--распадов.
Пользуясь таблицей Менделеева и правилами смещения, определить, в какой элемент превращается
 после шести α-
и трех β--распадов.
после шести α-
и трех β--распадов.Ядра радиоактивного изотопа тория
 претерпевают последовательно α-распад,
два β--распада
и α-распад.
Определить конечный продукт деления.
претерпевают последовательно α-распад,
два β--распада
и α-распад.
Определить конечный продукт деления.Определить, сколько β- и α-частиц выбрасывается при превращении ядра таллия
 в ядро свинца
в ядро свинца
 .
.
Радиоактивный изотоп радия
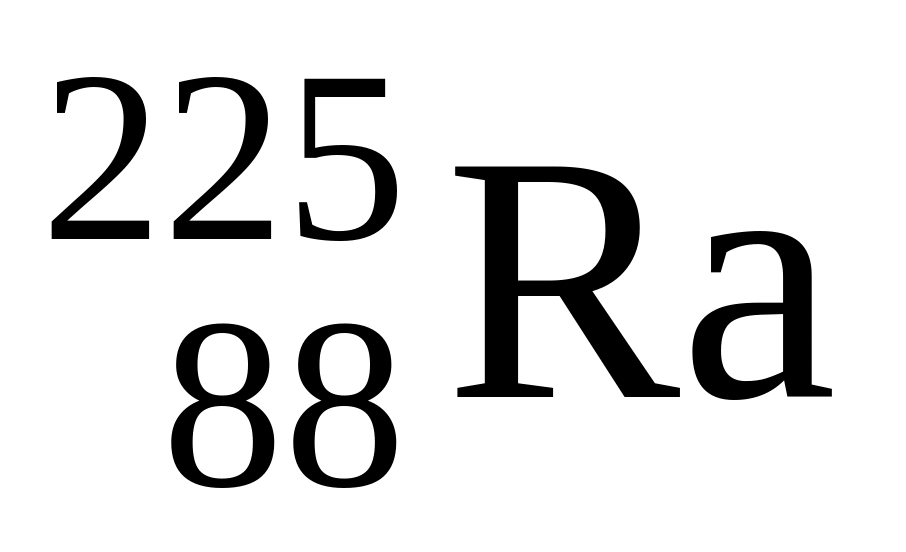 претерпевает четыре α-распада
и два β--распада.
Определить для конечного ядра: 1)
зарядовое число Z;
2) массовое число А.
претерпевает четыре α-распада
и два β--распада.
Определить для конечного ядра: 1)
зарядовое число Z;
2) массовое число А.
Записать α-распад радия .
Покоившееся ядро радона
 испускает α-частицу,
имеющую скорость 16 Мм/с. Зная, что масса
дочернего ядра составляет 3,62·10-25кг,
определить: 1) импульс α-частицы;
2) кинетическую энергию α-частицы;
З) импульс отдачи дочернего ядра; 4)
кинетическую энергию отдачи дочернего
ядра.
испускает α-частицу,
имеющую скорость 16 Мм/с. Зная, что масса
дочернего ядра составляет 3,62·10-25кг,
определить: 1) импульс α-частицы;
2) кинетическую энергию α-частицы;
З) импульс отдачи дочернего ядра; 4)
кинетическую энергию отдачи дочернего
ядра.
Покоившееся ядро полония
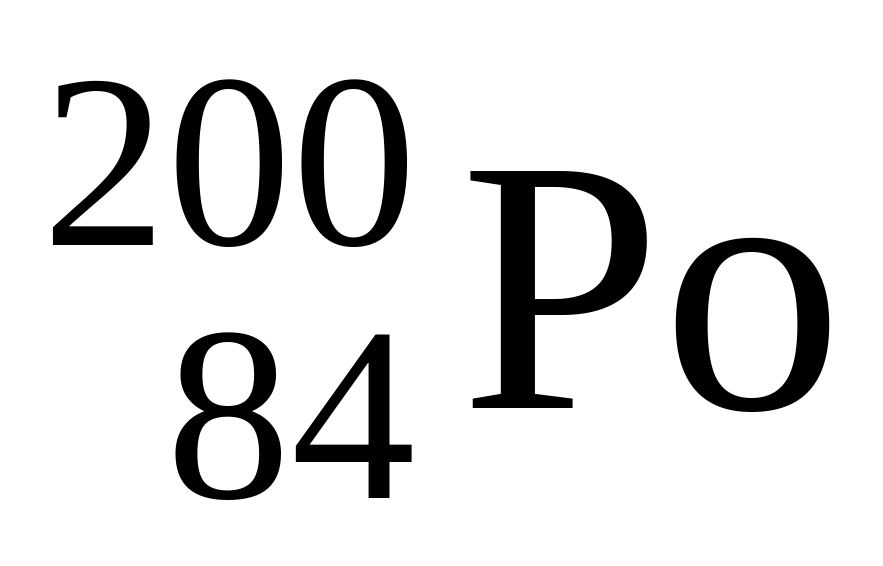 испускает α-частицу
с кинетической энергией Тα
= 5,77 МэВ. Определить: 1) скорость отдачи
дочернего ядра; 2) какую долю кинетической
энергии α-частицы
составляет энергия отдачи дочернего
ядра.
испускает α-частицу
с кинетической энергией Тα
= 5,77 МэВ. Определить: 1) скорость отдачи
дочернего ядра; 2) какую долю кинетической
энергии α-частицы
составляет энергия отдачи дочернего
ядра.
Определить энергию, выделяющуюся в результате реакции
 .
Массы нейтральных атомов магния и
натрия соответственно равны 3.8184.10-26
и 3.8177.10-26кг.
.
Массы нейтральных атомов магния и
натрия соответственно равны 3.8184.10-26
и 3.8177.10-26кг.
Записать β--распад магния .
Известно, что β--активные ядра обладают до распада и после него вполне определенными энергиями, в то же время энергетический спектр β--частиц является непрерывным. Объяснить непрерывность энергетического спектра испускаемых электронов.
Объяснить, почему существование антинейтрино полностью позволяет объяснить все особенности β--распада.
Объяснить, почему при α-распаде одинаковых ядер энергии α-частиц одинаковы, а при β--распаде одинаковых ядер энергии электронов различны.
Применяя понятия квантовой статистики, объяснить, почему невозможно принципиально создать «нейтринный лазер».
Описать основные процессы, происходящие при взаимодействии γ-излучения с веществом.
Свободное покоившееся ядро
 (m
= 317.10953.10-27кг)
с энергией возбуждения E = 129 кэВ
перешло в основное состояние, испустив
γ-квант.
Определить изменение энергии γ-кванта,
возникающее в результате отдачи ядра.
(m
= 317.10953.10-27кг)
с энергией возбуждения E = 129 кэВ
перешло в основное состояние, испустив
γ-квант.
Определить изменение энергии γ-кванта,
возникающее в результате отдачи ядра.Назвать два важных механизма, которыми можно объяснить ослабление потока фотонов с энергией Е = 500 кэВ при его прохождении через вещество.
Объяснить, где и почему лучше исследовать длинные цепи рождений и распадов частиц высоких энергий – в камере Вильсона или в пузырьковой камере.
Определить, является ли реакция
 экзотермической или эндотермической.
Определить энергию ядерной реакции.
экзотермической или эндотермической.
Определить энергию ядерной реакции.
Определить, поглощается или выделяется энергия при ядерной
 .
Определить эту энергию.
.
Определить эту энергию.
Определить, выделяется или поглощается энергия при ядерной реакции
 .
Массы ядер, участвующих в реакции:
.
Массы ядер, участвующих в реакции:
 = 7.2992·10-26кг,
= 7.2992·10-26кг,
 = 1.6736·10-227кг,
= 1.6736·10-227кг,
 = 6.8021·10-27кг,
= 6.8021·10-27кг,
 = 6.6467.10-27кг.
= 6.6467.10-27кг.Определить, выделяется или поглощается энергия при ядерной реакции
 .
Массы ядер, участвующих в реакции:
.
Массы ядер, участвующих в реакции:
 = 2.3253·10-26кг,
= 6.6467·10-27кг,
= 1.6737·10-27кг,
= 2.3253·10-26кг,
= 6.6467·10-27кг,
= 1.6737·10-27кг,
 = 2.8229.10-26кг.
= 2.8229.10-26кг.Определить зарядовое число Z и массовое число А частицы, обозначенной буквой х, в символической записи ядерной реакции: 1)
 ;
2)
;
2)
 ;
3)
;
3)
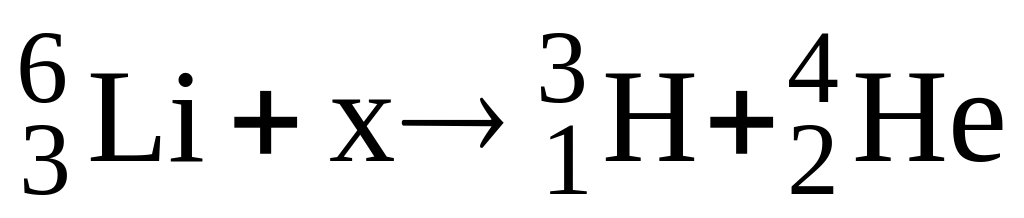 .
.Записать недостающие обозначения x в следующих ядерных реакциях: 1)
 (n,
α)х;
2)
(n,
α)х;
2)
 (α,
n)х;
3) x(p,
n)
(α,
n)х;
3) x(p,
n) ;
4)
;
4)
 (x, p)
(x, p) ;
5) x(n,
α)
;
5) x(n,
α)
 .
.В ядерной реакции
 выделяется энергия ΔE = 3,27 МэВ.
Определить массу атома
,
если масса атома
выделяется энергия ΔE = 3,27 МэВ.
Определить массу атома
,
если масса атома
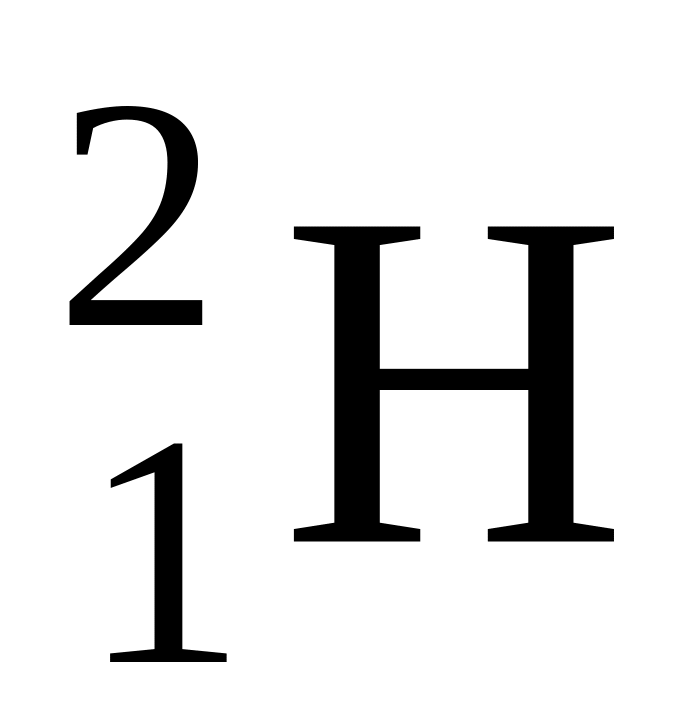 равна 3.34461·10-27кг.
равна 3.34461·10-27кг.
Жолио-Кюри облучали алюминий
 α-частицами,
в результате чего испускался нейтрон
и образовывалось искусственно-радиоактивное
ядро, испытывающее β+-распад..
Записать эту реакцию.
α-частицами,
в результате чего испускался нейтрон
и образовывалось искусственно-радиоактивное
ядро, испытывающее β+-распад..
Записать эту реакцию.Жолио-Кюри облучали магний
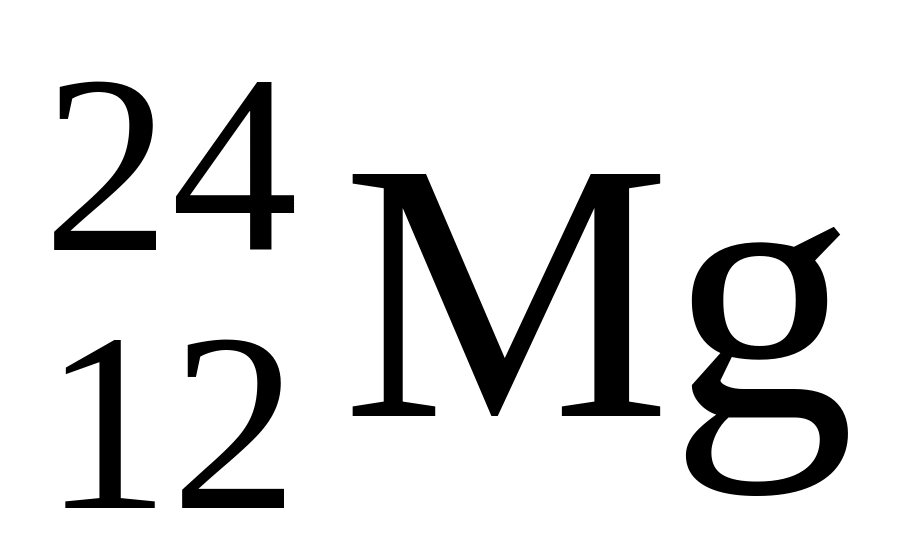 α-частицами,
в результате чего испускался нейтрон
и образовывалось искусственно-радиоактивное
ядро, испытывающее β+-распад.
Записать данную реакцию.
α-частицами,
в результате чего испускался нейтрон
и образовывалось искусственно-радиоактивное
ядро, испытывающее β+-распад.
Записать данную реакцию.В процессе осуществления реакции γ
 энергия E0
фотона составляла 2.02 МэВ. Определить
суммарную кинетическую энергию позитрона
и электрона в момент их возникновения.
энергия E0
фотона составляла 2.02 МэВ. Определить
суммарную кинетическую энергию позитрона
и электрона в момент их возникновения.
При столкновении позитрона и электрона происходит их аннигиляция, в процессе которой электронно-позитронная пара превращается в два γ-кванта, а энергия пары переходит в энергию фотонов. Определить энергию каждого из возникших фотонов, принимая, что кинетическая энергия электрона и позитрона до их столкновения пренебрежимо мала.
Записать схему электронного захвата (е-захвата) и объяснить его отличие от β±-распадов. Привести пример электронного захвата.
Дополнить недостающие обозначения x в следующих ядерных реакциях:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() .
.
Ядро урана
 ,
захватывая быстрый нейтрон, превращается
в радиоактивный изотоп урана, который
претерпевает β--распад,
и превращается в трансурановый элемент,
который в свою очередь также претерпевает
β--распад,
в результате чего образуется плутоний.
Записать все эти процессы в виде ядерной
реакции.
,
захватывая быстрый нейтрон, превращается
в радиоактивный изотоп урана, который
претерпевает β--распад,
и превращается в трансурановый элемент,
который в свою очередь также претерпевает
β--распад,
в результате чего образуется плутоний.
Записать все эти процессы в виде ядерной
реакции.Определить кинетическую энергию Т и скорость V теплового нейтрона при температуре окружающей среды, равной 17 °С.
Ядро урана, , захватывая тепловой нейтрон, делится на два осколка с массовыми числами 95 и 139, второй из которых, являясь радиоактивным, претерпевает три β--распада. Записать реакцию деления, а также цепочку β--распадов.
При захвате теплового нейтрона ядром урана образуются два осколка деления и два нейтрона. Определить порядковый номер Z и массовое число А одного из осколков, если другим осколком является ядро стронция
 .
.Объяснить, почему деление ядер должно сопровождаться выделением большого количества энергии.
Определить энергию (в электрон-вольтах), которую можно получить при расщеплении 1г урана , если при расщеплении каждого ядра урана выделяется энергия 200 МэВ.
Определить суточный расход чистого урана атомной электростанцией тепловой мощностью P = 300 МВт, если энергия E, выделяющаяся при одном акте деления, составляет 200 МэВ.
Определить число нейтронов, возникающих за 1 с в ядерном реакторе тепловой мощностью P = 200 МВт, если известно, что при одном акте деления выделяется энергия E = 200 МэВ, а среднее число нейтронов на один акт деления составляет 2.5.
Объяснить, почему реакция синтеза атомных ядер – образование из легких ядер более тяжелых – является колоссальным источником энергии.
Объяснить, почему для протекания термоядерной реакции необходимы очень высокие температуры.
