1. Интерференция света

1. Некогерентные волны I = I₁ + I₂;

2. Когерентные волны I = 2I₀ + 2I₀cosδ;

3. Оптическая разность хода для минимума ;

4. Оптическая разность хода для максимума ;

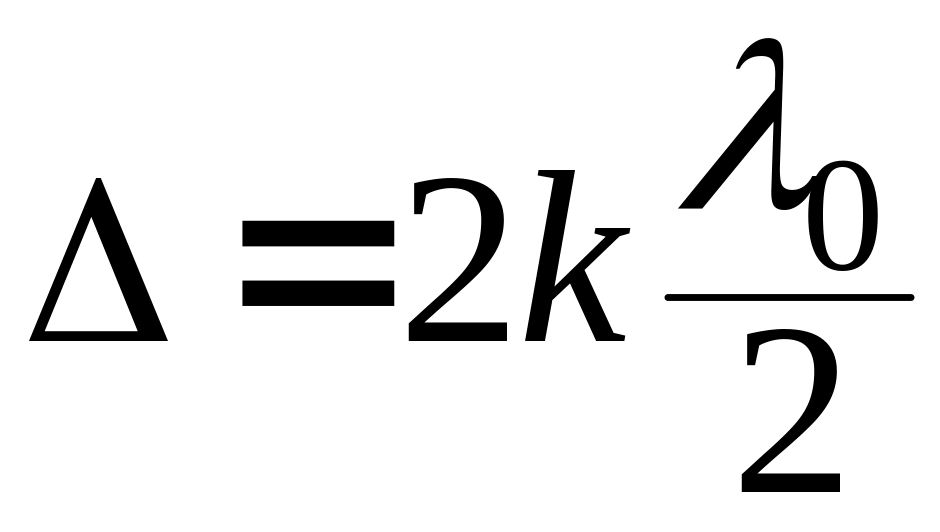5. Когерентными являются волны, у которых:

1. ω₁ = ω₂ или ν₁ = ν₂ ,

2. φ₁ - φ₂ = const,

3. E₁║E₂.

6.Длину цуга можно оценить по формуле длина цуга , где λ – средняя длина волны цуга волн, ∆λ – диапазон длин волн в цуге.

7.Радиус когерентности r_ког~/.

где  — длина световых волн,  — угловой размер источника.

8. Кольца Ньютона (в отражённом свете)

,

;

9.Тонкая плёнка -

максимум,

минимум;

10.Клин 2nℓα = λ;

11. координаты максимумов в схеме Юнга;

12. расстояние между полосами в схеме Юнга.

Примеры решения задач

Пример 1. Два параллельных пучка световых волн I и II падают на стеклянную призму с преломляющим углом θ = 30° и после преломления выходят из нее . Найти оптическую разность хода Δ световых волн после преломления их призмой (b = 2см).

Решение

Д ано:

θ = 30°

b = 2см

Δ = ?

Из рисунка видно, что Δ = (FD·n − ΒΕ), но BE = BD·sinφ = ,

откуда , т.е. призма не вносит дополнительной разности хода в проходящие через неё лучи.

Ответ: ∆ = 0

Пример 2. Оптическая разность хода Δ двух интерферирующих волн монохроматического света равна 0.3λ. Определить разность фаз δ.

Решение

Д ано:

Δ = 0.3λ

δ - ?

Запишем уравнение бегущей волны y(x,t) = A∙sin(ωt − kx). Выражение в скобках (ωt − kx) = φ –фаза колебания. Заметим, что для всех точек волны величины ω и t одинаковы. Поэтому разность фаз колебаний двух точек волны с координатами x₁ и x₂ будет:

δ = φ₂ − φ₁ = k(x₂ − x₁) = k∙Δ. Здесь - волновое число. Окончательно .

Откуда δ =

Ответ: .

Пример 3. Расстояние d между двумя когерентными источниками света (λ = 0.5 мкм) равно 0.1мм. Расстояние b между интерференционными полосами на экране в средней части интерференционной картины равно 1см. Определить расстояние от источников до экрана.

Решение

Дано:

d = 0.1мм

λ = 0.5 мкм

b = 1см.

ℓ - ?

Оптическая схема Юнга показана на рисунке (именно она используется в задаче). Два точечных когерентных источника А и В (щели, перпендикулярные плоскости рисунка), находятся на расстоянии d друг то друга и на расстоянии ℓ от экрана. S₁ и S₂ – расстояния от источников до произвольной точки экрана С, находящейся на расстоянии х от его центра. Если считать, что лучи распространяются в воздухе (n = 1), то оптическая разность хода лучей от источников до точки С будет

∆ = S₂− S₁

Рассматривая ∆АСЕ и ∆ABD и используя теорему Пифагора, можно получить:

,

.

Вычитая первое уравнение из второго, получаем:

.

, a (т.к. интерференционная картина может наблюдаться только в центре экрана, в этом случае оптическая разность хода не будет большой).

Положение светлых полос (максимумов) на экране будет определяться условием: , откуда координаты максимумов будут: .

Расстояние между соседними полосами

Это расстояние не зависит от х, т.е. на экране будет наблюдаться ряд параллельных равноотстоящих полос.

В задаче обозначено b = Δx. Отсюда . Окончательно

Ответ: 2м.

Пример 4. Между двумя плоскопараллельными стеклянными пластинками положили очень тонкую проволочку, расположенную параллельно линии соприкосновения пластинок и находящуюся на расстоянии ℓ = 75мм от нее. В отраженном свете на верхней пластинке видны интерференционные полосы. Определить диаметр d поперечного сечения проволочки, если на протяжении а = 30мм насчитывается m = 16 светлых полос.