Решение

Д ано:

λ = 600нм

τ = 10^-8с

∆λ = ?

В данном случае используем соотношение неопределённостей для времени и энергии:

∆t·∆E ≥ ħ или τ·∆E ≥ ħ. . Энергия фотона ε связана с длиной волны λ соотношением (знак минус в данном случае опущен). Окончательно . Таким образом, диаграмма энергетических уровней атома более корректно должна выглядеть так:

Бесконечно узким будет только первый уровень (для него , т.к. τ = ∞, устойчивое состояние, в котором атом может находиться бесконечно долго), остальные (возбуждённые) уровни уширены (это естественная ширина энергетических уровней и, соответственно, естественная ширина спектральных линий). Однако, если сравнить λ и ∆λ, то можно видеть, что λ >> ∆λ и во многих случаях это уширение можно не учитывать. Существуют другие причины уширения спектральных линий, приводящие к уширению на порядки большему, чем естественная ширина. Например, тепловое движение атомов приводит к большему на порядок уширению за счёт эффекта Доплера. Чтобы устранить доплеровское уширение нужно остановить тепловое движение атомов, это можно сделать, охладив атомы до абсолютного нуля температуры (Т = 0ºК).

Ответ:

Пример 5. Используя соотношение неопределённостей, оценить минимально возможную полную энергию электрона в атоме водорода, если неопределённость координаты равна радиусу атома.

Решение

Дано:

∆x = r

n = 1

Z = 1

Используем соотношение неопределённостей ∆x·∆p_x ≥ ħ. Согласно теории Бора полная энергия электрона в атоме водорода

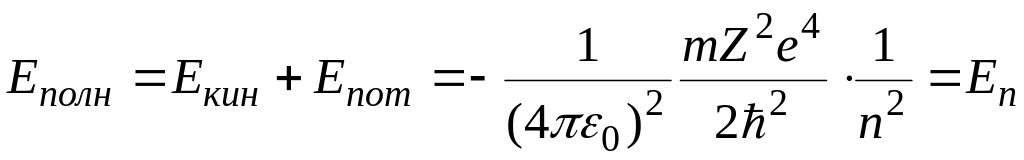
В данном случае

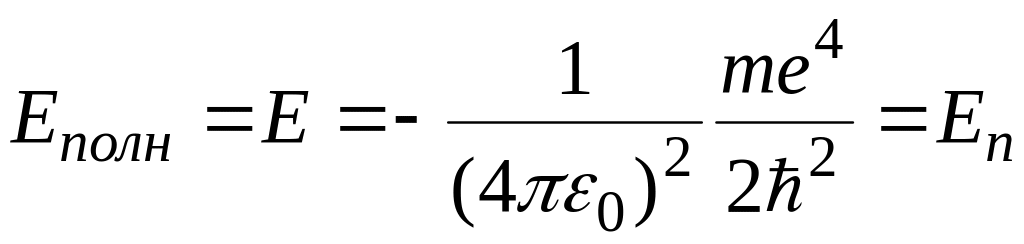
Сделаем замену (см. пример3) и ∆p = p, . Далее 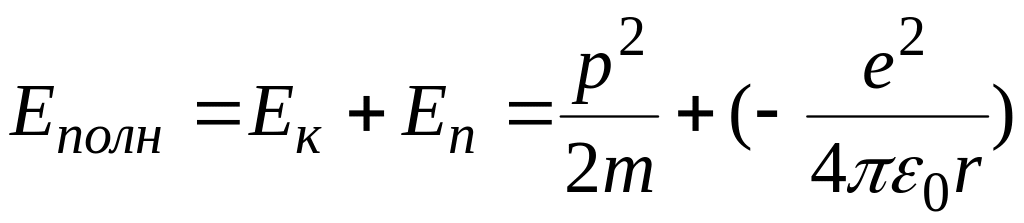. Из соотношения неопределённостей . Отсюда полная энергия будет 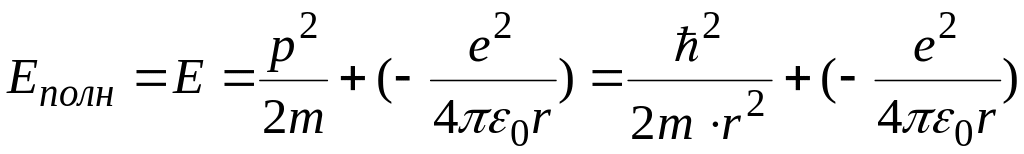, т.е. получили . Для нахождения исследуем эту функцию на экстремум.

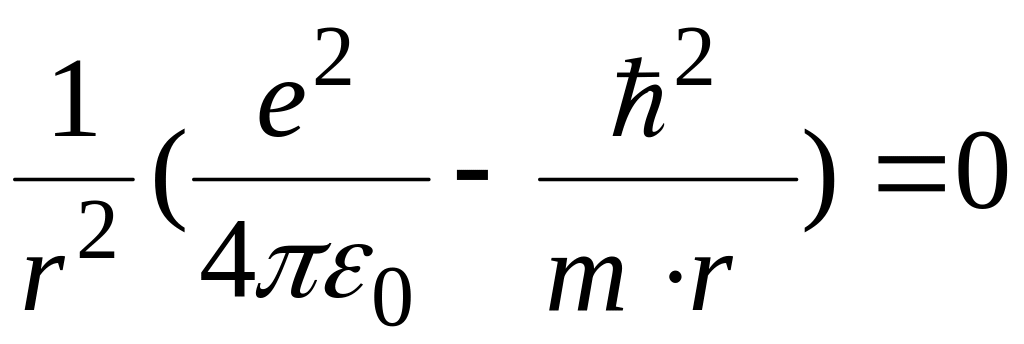
, откуда

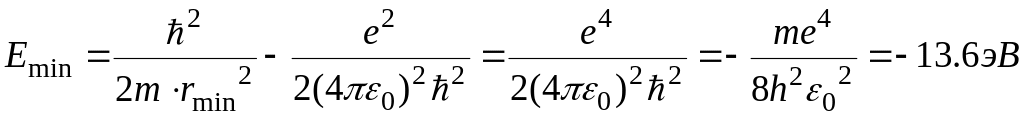
Ответ: .

Пример 6. Частица массой m находится в одномерной бесконечно глубокой прямоугольной потенциальной яме шириной d. Определить вероятность найти частицу в средней трети ямы, если она находится в основном состоянии.

Решение

Д ано:

m

n = 1

d

W = ?

Волновая функция микрочастицы внутри прямоугольной бесконечно глубокой потенциальной ямы имеет вид:

, следовательно

W=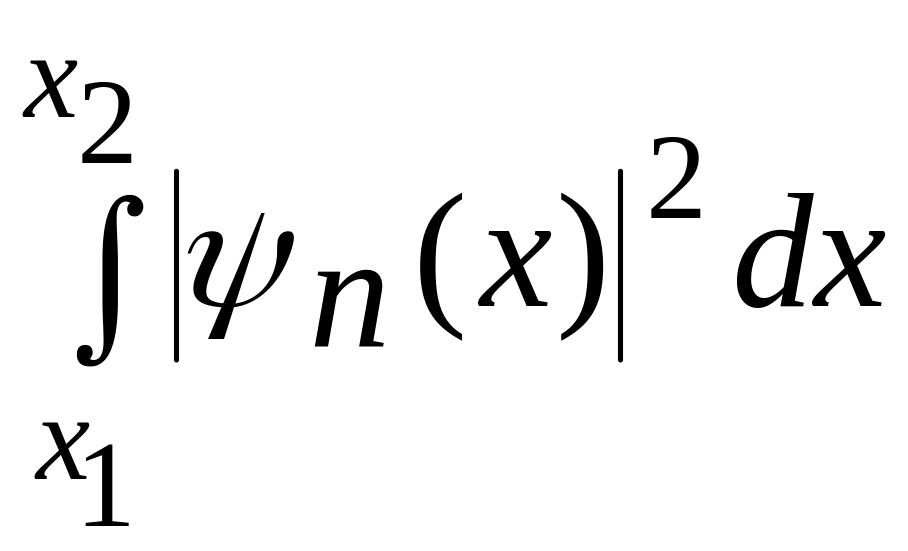

Далее

,

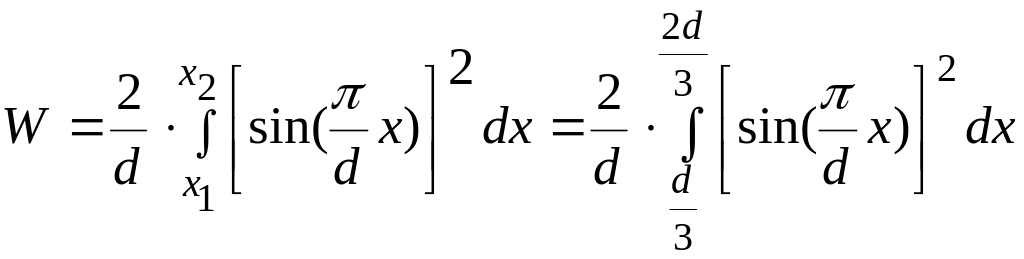
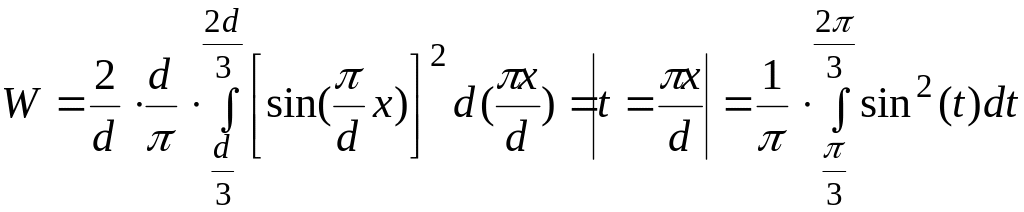но

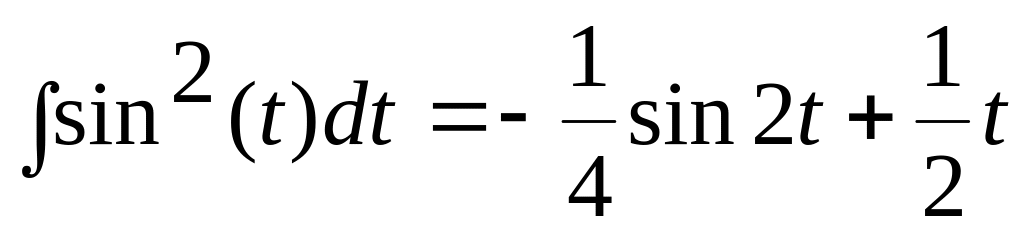
Откуда

Ответ:

Пример 7. Электрон в атоме находится в d – состоянии. Найти наименьший угол φ, который может составлять орбитальный момент импульса электрона в атоме c направлением внешнего магнитного поля. Сколько существует возможных его ориентаций.

Р z ешение

Д ано:

d – состояние

φ_min = ?

n = ?

Орбитальный момент импульса электрона в атоме L можно рассчитать по формуле . В зависимости от значения орбитального квантового числа ℓ состояния электрона в атоме обозначаются s,p,d,f и т.д.

состояние	s	p	d	f
ℓ =	0	1	2	3

В d – состоянии ℓ = 2, следователь магнитное квантовое число m может принимать значения m = 0, ±1,±2. Значение квантового числа m определяет величину проекции вектора на направление внешнего поля (т.е. задаёт возможные ориентации вектора в пространстве). -проекция момента импульса. В данном случае , т.е. может принимать 5 значений. Из рисунка ясно, что угол φ минимален, когда . Откуда cos (φ_min) = . 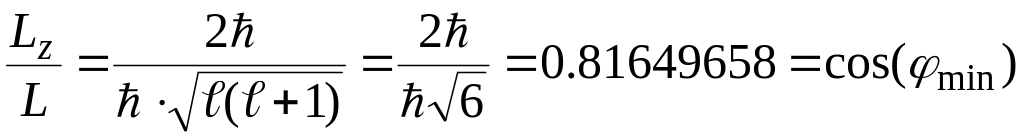Откуда .

Ответ: 5 значений, .

Пример 8. Найти коэффициент прозрачности D барьера высотой U₀ = 5эВ для электрона с энергией Е = 4.9эВ, если ширина барьера d = 0.1нм. При какой ширине d барьера вероятность прохождения электрона через него W будет равна 0.2?