21.2. Закон Ома. Законы Кирхгофа.
Закон
Ома для всей цепи
выражает соотношение между электродвижущей
силой (ЭДС), сопротивлением и током.
Согласно этому закону ток в замкнутой
цепи равен ЭДС источника деленной на
сопротивление всей цепи:
,
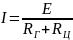где
I
- ток, протекающий по цепи; E
- ЭДС, генератора, подключенного к
электрической цепи; Rг
- сопротивление генератора; Rц
- сопротивление цепи. Закон
Ома для участка цепи.
Ток на участке цепи прямо пропорционален
напряжению между началом и концом
участка и обратно пропорционален
сопротивлению участка. Аналитически
закон выражается в следующем виде:
, где I
- ток, протекающий на участке цепи; R
- сопротивление участка цепи; U
- напряжение на участке цепи. Обобщенный
закон Ома.
Сила тока в контуре цепи прямо
пропорциональна алгебраической сумме
ЭДС всех источников цепи и обратно
пропорциональна арифметической сумме
всех активных сопротивлений цепи:
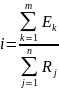, где m
и n
– количество источников и резисторов
в контуре цепи. При алгебраическом
суммировании со знаком “”
берутся те ЭДС, направление которых
совпадает с направлением тока, а со
знаком “–”
– те ЭДС, направление которых не совпадает
с направлением тока.
Первый
закон Кирхгофа.
Сумма
величин токов, притекающих к точке
разветвления, равна сумме величин токов,
утекающих от нее.
Это положение и является формулировкой
первого закона Кирхгофа. Условимся
токи, притекающие к точке разветвления,
считать положительными, а токи, утекающие
от нее, - отрицательными и сформулируем
окончательно первый закон Кирхгофа:
Алгебраическая
сумма величин токов в точке разветвления
равна нулю
или
.
Второй
закон Кирхгофа.
Второй закон Кирхгофа связывает между
собой ЭДС, действующие в любом
замкнутом
контуре, и падения напряжения на
сопротивлениях, входящих в данный
контур. Алгебраическая
сумма ЭДС, действующих в любом замкнутом
контуре, равна алгебраической сумме
падений напряжения на всех участках
этого контура
или
.
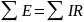21.3.
Зная значение напряжение полной шкалы, мы можем найти напряжения, соответствующие каждому разряду. В нашем случае Uпш=10В и количество разрядов n=6:
N разряд = Uпш/2N, N ;
1 разряд = 5В; 2 разряд = 2,5В;
3 разряд = 1,25В; 4 разряд = 0,625В;
5 разряд = 0,3125В; 6 разряд = 0,15625В;
Зная цифровой код на входе ЦАП можно найти напряжение на выходе:
101011 -> Uвых= 5+1,25+0,3125+0,15625= 6,71875В.
22.1. Счетчик, определение. Классификация.
Счетчиком называется схема, выполняющая функции подсчета количества единичных сигналов, поступивших на ее вход, а также функции формирования и запоминания некоторого кода, соответствующего этому количеству. Счетчики также иногда могут выполнять функции приема и выдачи кода. Схемы счетчиков можно классифицировать по следующим признакам: Основание системы счисления. В вычислительных системах используются двоичные и десятичные счетчики. Двоичные счетчики в свою очередь подразделяются на счетчики с модулем пересчета равным 2n и модулем пересчета, не равным 2n, где n - разрядность счетчика. Направление переходов счетчика. Счетчики принято разделять на простые (суммирующие или вычитающие), которые могут вести счет только в одном направлении, то есть только прибавлять или вычитать входные сигналы, и реверсивные, которые в зависимости от управляющих сигналов могут вести счет в прямом или обратном направлениях. Способ построения цепей переноса. Различают счетчики с последовательным, сквозным, параллельным и групповым переносом. Способ организации счета. Счетчики могут быть асинхронными и синхронными. В асинхронных счетчиках изменение состояния счетчика осуществляется с поступлением информации только на вход первого каскада. В синхронных счетчиках информационный сигнал поступает одновременно на синхронные входы всех разрядов. Тип элементов, используемых для построения счетчика. Различают счетчики на импульсных, импульсно-потенциальных и потенциальных элементах. Тип организации счетного элемента. Счетчики могут быть построены на триггерах со счетным входом и на запоминающих элементах с использованием логических суммирующих схем.
Отдельно – счетчики, работающие по принципу циклического сдвигающего регистра, но они практически не применяются.