
Шпаргалка на ряды Фурье и комплексную переменную / matdefs4шпора
.doc1. Тригонометрический ряд: a0+n=1(ancos nx+bnsin nx) (1)
Теорема: Пусть ряд (1) равномерно сходится
на [0,2]
к некоторой f(x)=(1), тогда
a0=![]() an=
an=![]() ;
bn=
;
bn=![]()
a0, an, bn – определены однозначно.
Если f(x) определена на всей оси, f(x+2)=f(x), ограничена на всей оси, интегрируема по Риману на [0,2], то a0, an, bn – коэффициенты ряда Фурье.
Частичные суммы: Sn(x)=a0+n=1(ancos
nx+bnsin
nx)=…=
![]() =
=
![]() ,
где Dn(y)
– ядро Дирихле. Dn(y)=
,
где Dn(y)
– ядро Дирихле. Dn(y)=
 ;
y2kDN(2k)=N+½y
;
y2kDN(2k)=N+½y
![]() =…=
=…=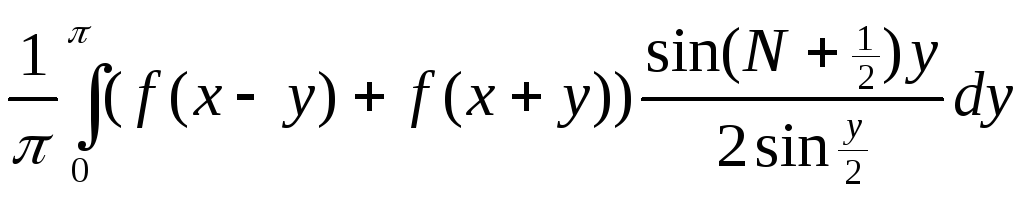 =Sn
=Sn
2. Sn(x)=
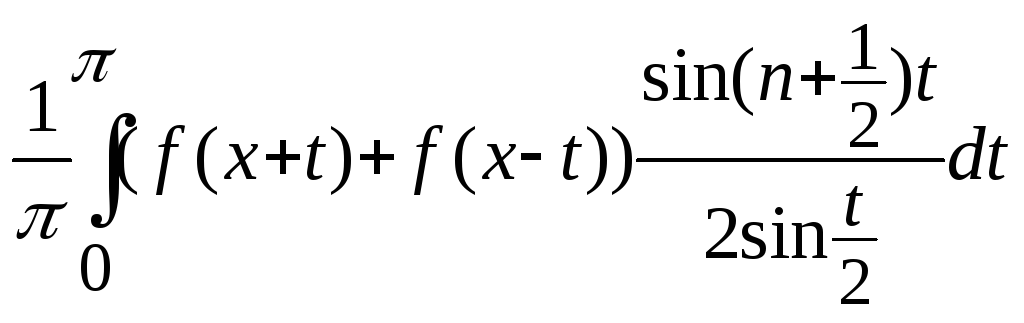 f(x)=
f(x)=
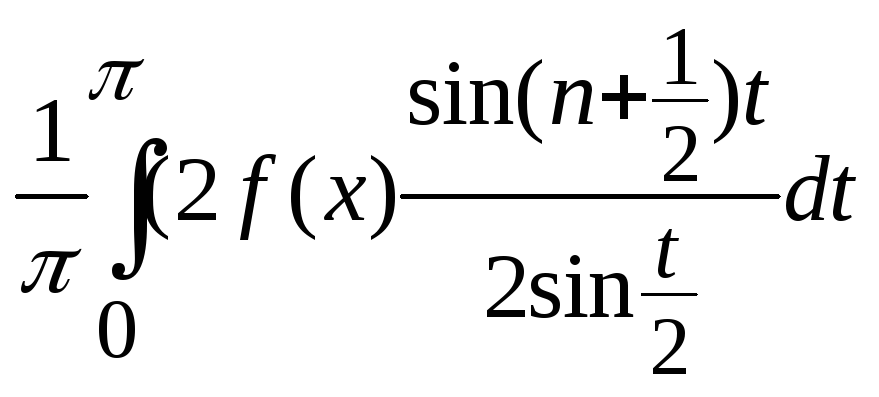
Sn(x)-f(x)=

Теорема: Для любой точки x существует функция, непрерывная на всей оси, с 2-периодом, такая что ее ряд Фурье расходится в точке x.
Признак Дини сходимости ряда Фурье в точке.
Утверждение: f – с периодом
,
непрерывна в точке x0.,
предположим, что
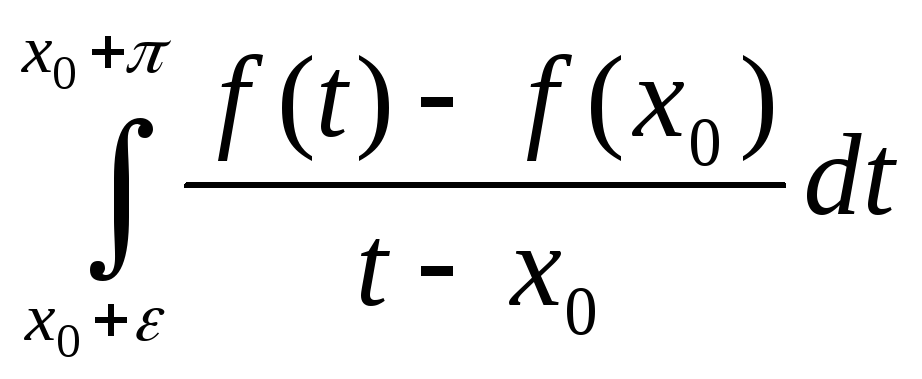 <M;
<M;
 <M,
тогда
<M,
тогда
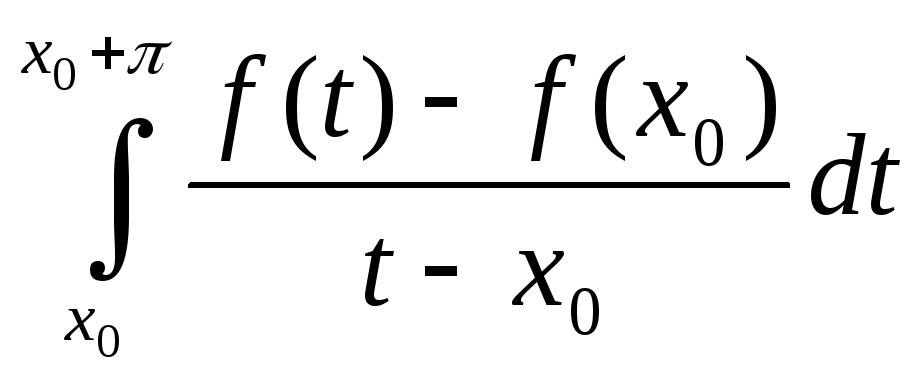 и
и
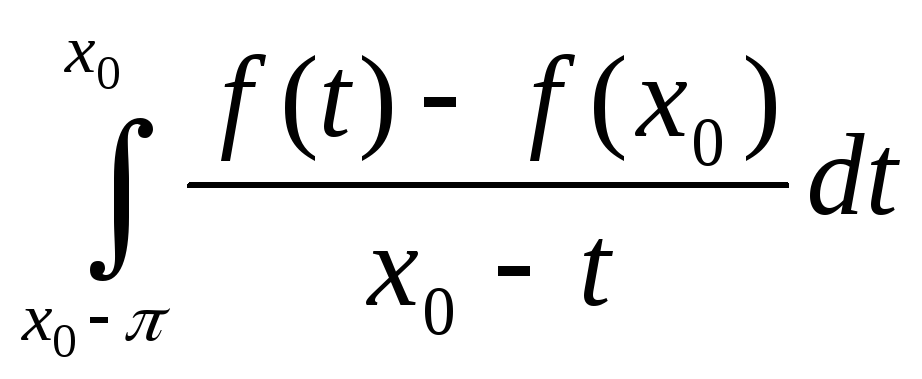 сходятся, тогда ряд Фурье для функции
f сходится в точке x0
к Функции f(x0).
сходятся, тогда ряд Фурье для функции
f сходится в точке x0
к Функции f(x0).
Лемма Римана: Допустим, h(x)
интегрируема по Риману на [a,b],
тогда
![]() ;
;
![]()
3. Признак Липшица: f-2 периодом, интегрируема на (-М,М), непрерывна в точке x0.
Пусть существует 0, c>0, 0<<1: для любых y, |y-x0|<0 справедливо соотношение:
|f(y)-f(x0)|<c|y-x0|. Тогда Ряд Фурье функции f в точке x0 сходится к значению f(x0).
Доказательство: проверить свойство
 <M.
<M.
Пример: f(x)=(-x)/2.
|f(y)-f(x)|=½|y-x|; a0=0,
an=0,
bn=1/n.
![]() x(0,2).
x(0,2).
4. Признак Дирихле-Жордана: Пусть функция определена на всей оси, 2-периодом.
Предположим, что [0,2]=nk=1[pk,qk]; (pk,qk)(pl,ql)=, kl такие, что f монотонна на каждом промежутке и ограничена на всем [0,2]. Тогда ряд Фурье в любой точке сходится к величине 1/2((lim f(t) при tx+0)+(lim f(t) при tx-0)).
5. Среднее Фейера:
![]() - числовой ряд,
- числовой ряд,
![]() =SN
=SN
N=(S1+…+SN)/N=![]() .
.
Говорят, что числовой ряд суммируем по Фейеру, если существует конечное число А: NA при N.
Теорема: Фейера Если ряд
![]() сходится
к сумме S, то суммируем по
Фейеру к тому же числу S.
сходится
к сумме S, то суммируем по
Фейеру к тому же числу S.
Пример: Раcсходимость
ряда:
![]() 2n=1/2;
2n-1=
2n=1/2;
2n-1=![]() n1/2
при n.
n1/2
при n.
6. Среднее Фейера для Ряда Фурье: f(x+2)=f(x), интегрируема по Риману на (-m,m).
N(x)=
![]() =a0+
=a0+![]() =
=
=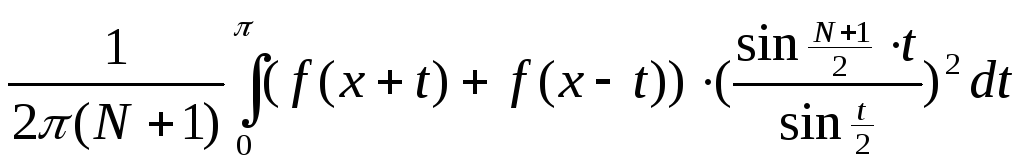
7. Выражение среднего Фейера через интеграл
N(x)=
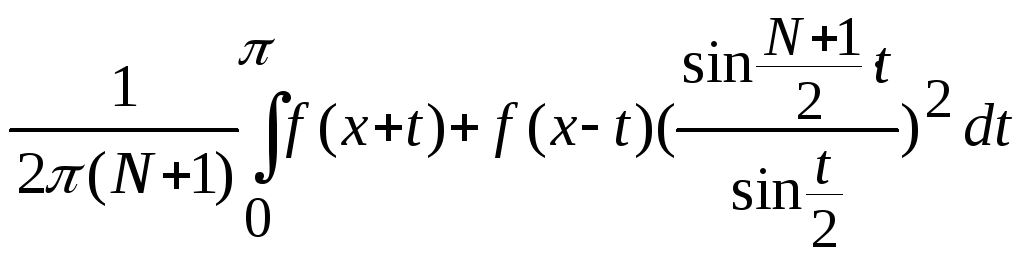 ;
f0(x)=1;
;
f0(x)=1;
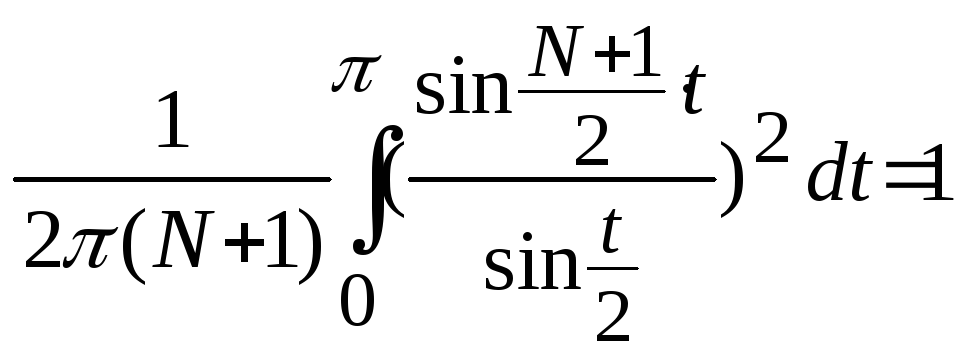
Ядро Фейера: FN(t)=
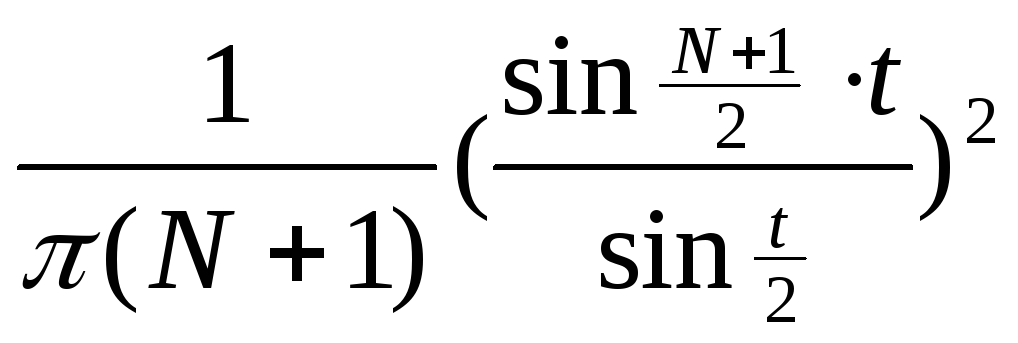 ;
;
![]() ;
FN(t)>0.
N(x)=
;
FN(t)>0.
N(x)=![]()
8. Теорема: Фейера
о непрерывности функции с 2
- периодом: Пусть f(x+)=f(x),
непрерывна на всей вещественной
оси, тогда N(x)
![]() f(x)
на всей вещественной оси.
f(x)
на всей вещественной оси.
9. Свойства линейности Среднего Фейера:
-
N(x,cf)=cN(x,f)
-
N(x,f+g)=N(x,t)+N(g).
-
|N(x,f)|<N(x,|f|).
-
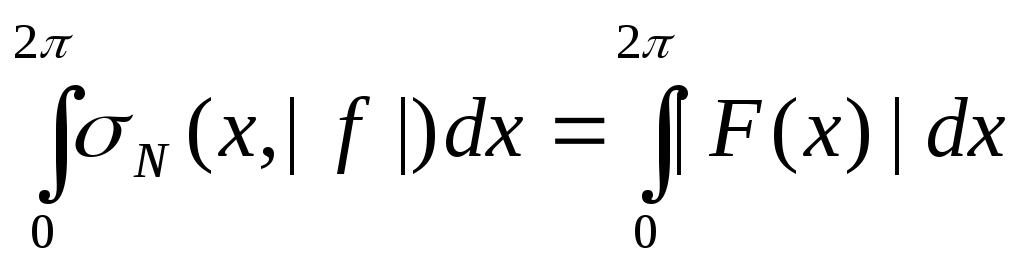 Следствие:
Следствие:
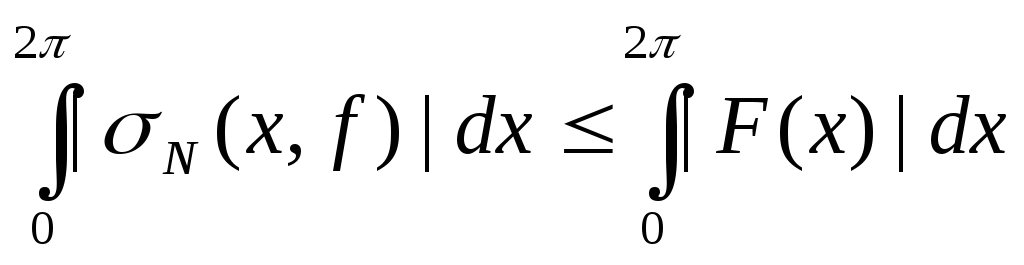
10. Утверждение:
f интегрируема на [a,b],
тогда >0
Существует
непрерывна на [a,b]:
(a)=(b)=0
и
![]() .
Из-за интегрируемости f
с использованием критерия
интегрируемости мы получаем, что
существует разбиение a=a0<a1<…<an=b
и такие точки tk[ak-1;ak]
т.ч.
.
Из-за интегрируемости f
с использованием критерия
интегрируемости мы получаем, что
существует разбиение a=a0<a1<…<an=b
и такие точки tk[ak-1;ak]
т.ч.
![]()
приближенно к f
кусочно-постоянной функции.
приближенно к f
кусочно-постоянной функции.
Пусть M=sup|f(x)|. Надо взять
=![]()
Следствие: Пусть f-2-период,
интегрируема (-m,m),
Тогда>0
существует (x+2)=(x)
![]() .
.
-
|f(x)|<M x => |N(x,f)|<M
11. Сходимость Среднего
Фейера в метрике L1:f
интегрируема на(-m,m)=>![]() .
Доказательство: используя теорему
Фейера для
существует N : n>N,
x :
|n(x,)-(x)|</2.
.
Доказательство: используя теорему
Фейера для
существует N : n>N,
x :
|n(x,)-(x)|</2.
Сходимость Среднего Фейера в метрике
L2:
f интегрируема на (-m,m)
![]()
12. Равенство Парсеваля
для тригонометрического многочлена:
![]()
13. Неравенство
Бесселя
![]() <
<![]()
14. Равенство Парсеваля
для произвольной интегрируемой по
Риману функции:
![]()
15. Ряды Фурье для функции с периодом Т: f(x)a0+n=1(ancos n2/Tx+bnsin n2/T x)
a0=![]() an=
an=![]() ;
bn=
;
bn=![]() ;
;
![]()
16. Пусть f
– комплекснозначна и
![]() -
сходится. Преобразованием Фурье
называется
-
сходится. Преобразованием Фурье
называется
![]() ,
свойства:
,
свойства:
1)
![]() ;
2)
;
2)
![]() ;
3)
a(x)=eiaxf(x),
a(x)=f(t-a);
4)
fa(x)=f(x+a),
fa(t)=eitaf(t);
f,g –комплекснозначные функции:
;
3)
a(x)=eiaxf(x),
a(x)=f(t-a);
4)
fa(x)=f(x+a),
fa(t)=eitaf(t);
f,g –комплекснозначные функции:![]() и
и![]() aбсолютно сходятся, тогда (x)=
aбсолютно сходятся, тогда (x)=![]() - свертка (fg)(x).
5)
- свертка (fg)(x).
5)
![]()
Обратное преобразование Фурье:
![]() g(t) определена на
всей вещественной оси
g(t) определена на
всей вещественной оси
17.
18. Лемма Римана несобственный
интеграл
![]() - сходится, тогда
- сходится, тогда![]() ;
;
![]()
Теорема (условия Дини для обращения
преобразования Фурье): f –
абсолютно интегрируема на всей оси,
![]() - сходится в некоторой точке x0R:
- сходится в некоторой точке x0R:
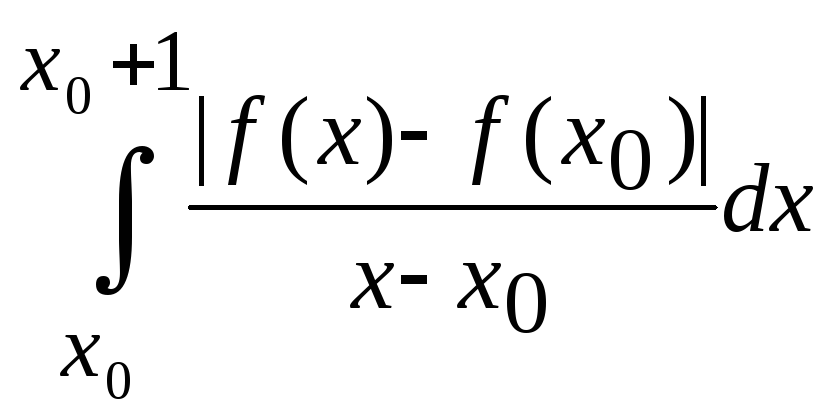 сходится и
сходится и
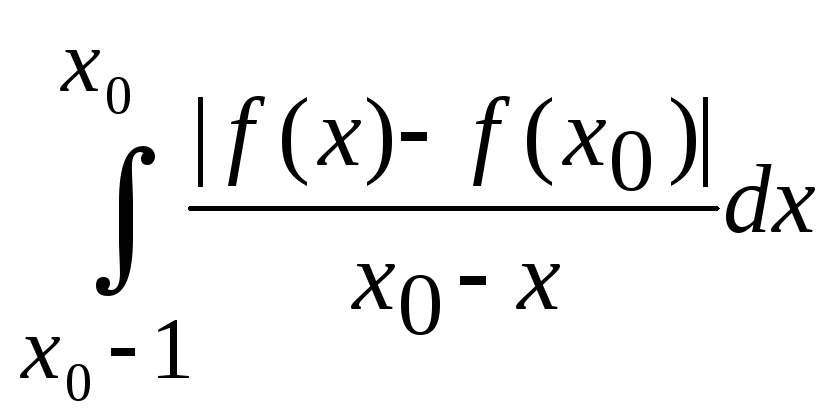
и
![]() ,
тогда существует
,
тогда существует
![]()
19. Равенство Пантереля :
f – абсолютно интегрируема на (-,),
тогда
![]()
20. f(x,y)=u(x,y)+iv(x,y). fx`(x,y)=ux`(x,y)+i vx`(x,y).
Свойства: 1) (сf)`x=c
fx`;
2) (f+g)`=fx`+gx`;
3) (fg)x`=fx`g+fgx`;
4) g(x,y)0;
![]() 5)
5)
![]()
Частная производная по z. fZ`(x,y)=½ (fx`(x,y)-i fy`(x,y)); f`(x,y)=½ (fx`(x,y)-i fy`(x,y));
Свойства те же.
21.
![]() - криволинейный интеграл II
рода.
- криволинейный интеграл II
рода.
![]()
Свойства: 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() 4)
4)
![]() - криволинейный интеграл I
рода
Двойной
интеграл.
- криволинейный интеграл I
рода
Двойной
интеграл.
![]()
22. Формула Грина
![]() ;
;
![]()
23. Аналитичность функция f*(x,y)=f(z); Функция f определена на аналитична на , f*, определена на D=J дифференцируема и непрерывна на D и справедливо f*`Z(M)=0 для MD.
Свойства: 1) f аналитична в => сf – аналитична в ; 2) f,g – аналитичны в => f+g, fg – аналитичны в ; 3) g(z)0 в , g – аналитична в , то 1/g – аналитична в ; 4) f,g0 аналитична в => f/g – аналитична в .
24. DC – открытое множество и f – аналитична в D. Для zD : f(z)G (открытое множество ) () аналитична в G h(z)=(f(z)) – аналитична.
25. A(D) – множество всех аналитичных функций (D – открытое непустое) fA(D) z=x+iyD выполяется система уравнений Коши-Римана {ux`=vy`; uy`=-vx`}
f=u(x,y)+iv(x,y)
ez=ex(cos y+i sin y); cos z=½ (eiz+e-iz); sin z=½i (eiz-e-iz); ln Z=ln|Z|+i argZ – главная ветвь логарифма. lnZ=ln|Z|+i arg Z+2ki; elnZ=Z; (ln Z)`=1/Z; Z=elnZ; elnZ=Z; ii=e/2; (z)`=az
27. Теорема Коши:
f аналитична на D (связанное
открытое ограниченное множество),
ограниченная границей Г (конечное число
кусочно-гладких кривых), f –
имеет непрерывные частные производные
fx`
и fy`
вплоть до границы D, тогда
![]() (+ ориентированная граница)
(+ ориентированная граница)
28. Формула Коши для
производной f `(z0)=
![]() 29.
29.
![]() =0;
=0;
30. Формула Коши для
n-ой производной
![]()
31. Неравенство Коши
={:|-a|=r},
R>r fА(Br(a)),
Пусть |f()|<M.
![]() ;
;
![]()
32.
![]() (сход. к своей
равномерно на Е, если Vn(z)=n(z)+in(z),
ряды
(сход. к своей
равномерно на Е, если Vn(z)=n(z)+in(z),
ряды![]() и
и![]() равномерно сходятся. Признак
Вейерштрасса |Vn(z)|<an
сходится равномерно.
равномерно сходятся. Признак
Вейерштрасса |Vn(z)|<an
сходится равномерно.
33. fA(Br(a))
zВR(a)
справедливо f(z)=f(a)+
![]() Ряд сходится на замкнутом круге
Ряд сходится на замкнутом круге![]()
34. Ряд Тейлора
ez=1+![]() ;
cos Z=1+
;
cos Z=1+![]() ;
sin Z=
;
sin Z=![]() ;ln(1+z)=
;ln(1+z)=
![]() ;
(1+z)r=1+
;
(1+z)r=1+![]()
35. Теорема Абеля:
Рассмотрим степенной ряд С0+
![]() .
Предположим, что ряд сходится в
точке z0a
R=|z0-a|.
Тогда ряд сходится в круге zBR(a)
и для 0<r<R
равномерно сходится в замкнутом
круге
.
Предположим, что ряд сходится в
точке z0a
R=|z0-a|.
Тогда ряд сходится в круге zBR(a)
и для 0<r<R
равномерно сходится в замкнутом
круге
![]() .
.
36. Ряд С0+
![]() .
1) Сходится, только при
z=a тогда =0;
2) Сходится при любых комплексных
z, тогда =;
3) za.
в которой ряд сходится и za
при которой ряд расходится
|z0-a|<<|z1-a|,
тогда при
|z-a|<
ряд сходится и при z*
: |z*-a|>
расходится
.
1) Сходится, только при
z=a тогда =0;
2) Сходится при любых комплексных
z, тогда =;
3) za.
в которой ряд сходится и za
при которой ряд расходится
|z0-a|<<|z1-a|,
тогда при
|z-a|<
ряд сходится и при z*
: |z*-a|>
расходится
![]()
37. Предположим,
что имеется степенной ряд
С0+
![]() и пусть >0,
тогда сумма ряда является аналитичной
в круге B(a).
и пусть >0,
тогда сумма ряда является аналитичной
в круге B(a).
38. Теоремы единственности для открытого круга: 1) R>0, fA(BR(a)) Пусть 0<r<R и f(z)=0 при zBr(a), тогда f=0 в BR(a); 2) fA(D), D – открытое, связное множество Br(a)D, f=0 при zBr(a) => f=0 в D; 3) D – связное, открытое множество fA(D) и f0 в D и пусть S={z0D : f(z0)=0}. Тогда множество S не может иметь точки сгущения внутри области D.
39. B`r(a)=Br(a)\{a}.
Предположим, что fA(B`r(a)),
тогда возможны 3 поведения функции
в области B`r(a):
1) <r,
>0
и M:z
B`(a)
выполняется |f(z)|<M,
тогда можно доопределить функцию
в точке а, так что fA(Br(a));
2) |f(z)|+
при za
функция f имеет в точке
a полюс; n>1
: ![]() ,
n называется порядком полюса функции
f в точке a. Если
n=1 – f имеет в точке а
простой полюс, иначе кратный полюс;
3) |f(z)| неограничена в окресности
точки а, но |f(z)|+
при za,
тогда f имеет в точке
а, существенно особую точку.пример:
g(z)=e1/(z-a).
,
n называется порядком полюса функции
f в точке a. Если
n=1 – f имеет в точке а
простой полюс, иначе кратный полюс;
3) |f(z)| неограничена в окресности
точки а, но |f(z)|+
при za,
тогда f имеет в точке
а, существенно особую точку.пример:
g(z)=e1/(z-a).
40. 0<<r<+
открытое кольцо B,r(a)={z:<|z-a|<r},
если 0<<r<+,
то замкнутое кольцо B,r(a)={z:<|z-a|<r}
и fA(B`R(a)).
Тогда 1) zB`R(a)
f может быть представлена,
f(z)=![]() +
+
![]() ,
где оба ряда сходятся;
2)При zB,r(a)
оба ряда в сходятся равномерно.
,
где оба ряда сходятся;
2)При zB,r(a)
оба ряда в сходятся равномерно.
![]() - ряд Лорана, C-1=resfa=
- ряд Лорана, C-1=resfa=![]() где
- любая окружность, содержащаяся в
области B`R(a)
c центром в точке a.
где
- любая окружность, содержащаяся в
области B`R(a)
c центром в точке a.
Теорема о вычетах fA(D\nk=1{ak})
и непрерывна до границы Г=D.
Rk>0
выберем круги
![]() и BRk(a)kl
BRl(a)=,
тогда
и BRk(a)kl
BRl(a)=,
тогда
![]()
42. Типы поведения: 1-му соответствует ряд Лорана C-n=0 n; 2-му C-n=0 для n>N С-N0; 3-му nk C-nk0
Принцип максимума. Пусть fA(D). Тогда |f(z)| не может иметь строго локального максимума при zD. Если при z0D достигает |f(z)| не строгого локального максимума, то f=const.
Следствие: Если f аналитична в D и f непрерывна в D, то maxzD|f(z)|=maxzD|f(z)| - максимум достигается на границе.
