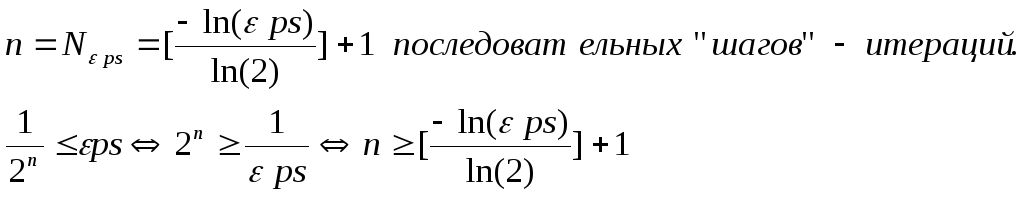Функции и их свойства / PAR12-13

§12.Точки разрыва функции и их классификация; вертикальная асимптота графика функции.

Из определения непрерывности функции в точке следуют

(2,3);;(1)

Свойства функции, непрерывной а точке:

1. aD_f –функция в точке определена; 2)a–предельная точка области определения >0:ПО(a;)D_f -любая проколотая окрестность содержит точки множества D_f ; 3)A_ЛЕВ,A_ПР,A_ЛЕВ=A_ПР=f(a)-существуют конечные односторонние пределы, равные значению функции в точке.

Определение 1. Точка aÎR называется точкой разрыва функции f, если она не является точкой ее непрерывности, т.е. не выполнено хотя бы одно из указанных условий (1-3).

Так как элементарные функции и их суперпозиции непрерывны во внутренних точках области определения, точками их разрыва могут быть либо граничные точки области определения, либо точки "сшивания", если значения функция задаются несколькими “формулами".

Определение 2. Точка х=a  разрыва функции f называется :

(1) точкой устанимого разрыва (т.у.р.), если ее односторонние пределы конечны и равны :

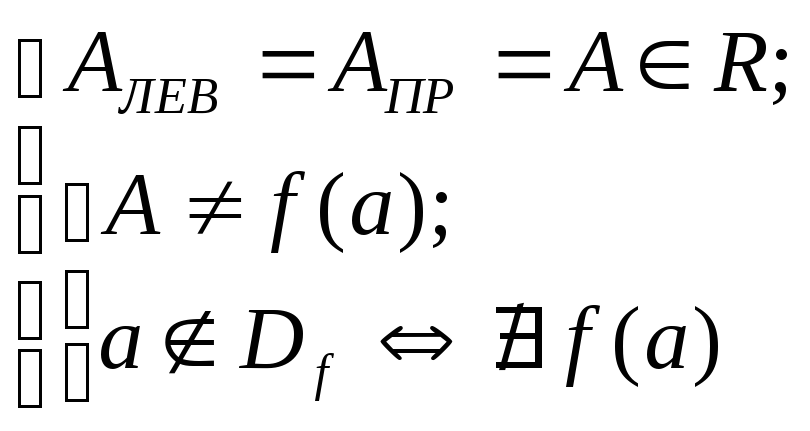
Разрыв в этой точке можно «устранить», если переопределить или доопределить значение функции в точке "a" «по непрерывности» : f(a)=A.

Например, f(x)=sin(x)/x x=0 –точка разрыва (0D_f);А_ЛЕВ=А_ПР=1точка устранимого разрыва доопределим f «по непрерывности»:

,  точка х=0 - точка непрерывности функции f^*.

2. точкой разрыва первого рода, если ее односторонние пределы конечны и не равны между собой : А_лев¹А_пр ("конечный скачок").

Например, для 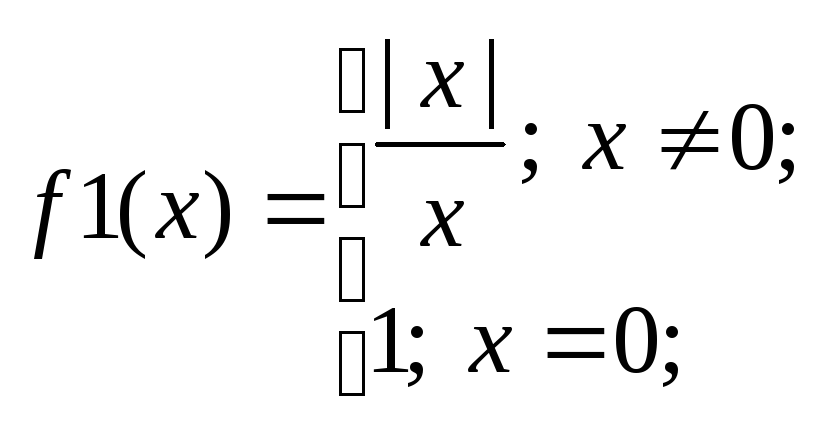точка х=0 - т.р. 1 рода,

т.к. А_лев=-1А_пр=+1;

3) точкой разрыва второго рода, если a - не т.у.р. и не т.р. I рода. (например, если хотя бы один односторонний предел бесконечен).

Например, для функции f(x)=1/(x-1) точка х=1 является т.р. 2 рода, так как А_лев=-∞; А_пр=+∞.

Определение 3. Если хотя бы один односторонний предел функции в точке "а" бесконечен, вертикальная прямая x=a называется вертикальной асимптотой графика функции y=f(x)(график "прижимается" к этой прямой при .

Например, прямая х=1 является вертикальной асимптотой графика y=f(x)=1/(x-1).

Замечание. Так как элементарные функции и их суперпозиции непрерывны во внутренних точках области определения D_f, точками их разрыва могут быть лишь «граничные» точки D_f или точки «сшивания»(если значения функции задаются несколькими выражениями -формулами).

------------------------------------------------------------------

Экз.задача. Исследовать непрерывность и точки разрыва функции; изобразить схематически "график функции" в окрестности точек разрыва; записать уравнения вертикальных асимптот графика.

f : R/{0,1}®R;

(1) Как суперпозиция элементарных функций функция f непрерывна "xÎR/{0,1)  точками разрыва могут быть лишь граничные точки : a1=0; a2=1.

(2) a1=0 : (а) 0ÏD_f Þ x=0- точка разрыва.

(б) А_{лев ,} А_пр : Þ a1=1 - точка разрыва 2 рода;  x=0 - левая и правая вертикальные асимптоты графика .

(3) a2=1:

x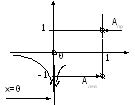

а1=0 - точка разрыва 2 рода;

х=0 - вертикальная асимптота графика;

а2=1 - точка разрыва 1 рода.

Задача 2.

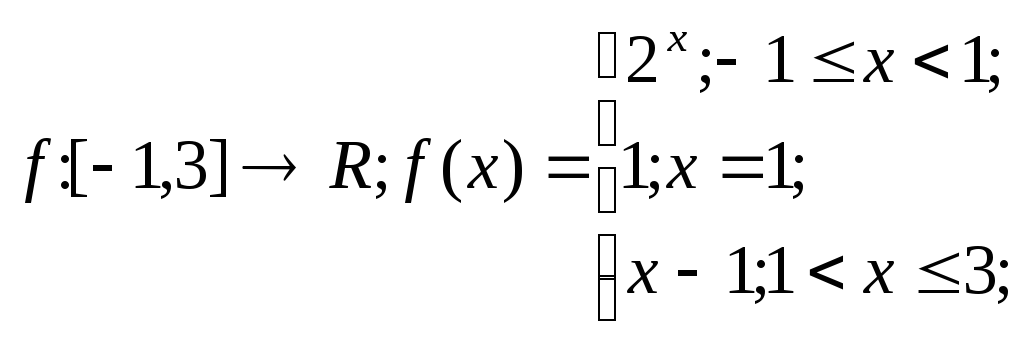
Итак, функция f непрерывна "x Î(-1,1) È (1,3); непрерывна справа в точке a1=-1; непрерывна слева в точке a3= 3; точка а2=1 - точка разрыва 1 рода.

§13. Свойства функций, непрерывных на замкнутом промежутке.

Пусть задана функция f : XRE_f R: f(x)

Определение 1. Функция f называется ограниченной на множестве Х, если ограничено множество ее значений E_f (X), при этом функцию называют

ограниченной снизу, если  график y=f(x) выше прямой ym;

ограниченной сверху, если  график y=f(x) ниже прямой yM;

ограниченной, если она ограничена снизу и сверху

Например, функция

Определение 2. Функция f называется непрерывной на множестве, если она непрерывна в каждой точке множества. Функция f называется непрерывной на замкнутом промежутке [a,b]D_f , если она непрерывна во внутренних точках , непрерывна справа в точке "а" и непрерывна слева в точке "b".

Свойства функций, непрерывных на замкнутом промежутке [a,b].

1) График y = f(x) функции, непрерывной на замкнутом промежутке [a,b],- непрерывная линия на координатной плоскости.

2)Теорема (Вейерштрасса). Функция, непрерывная на замкнутом промежутке [a,b] :(а) ограничена на этом промежутке

(б) принимает на этом промежутке свои наименьшее m=f_наим[a,b]=infE_f[a,b] и наибольшее M=f_наиб[a,b]=supE_f[a,b] значения

и(в) принимает на этом промежутке все значения от наименьшего m=f_наим до наибольшего М=fнаиб

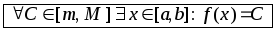
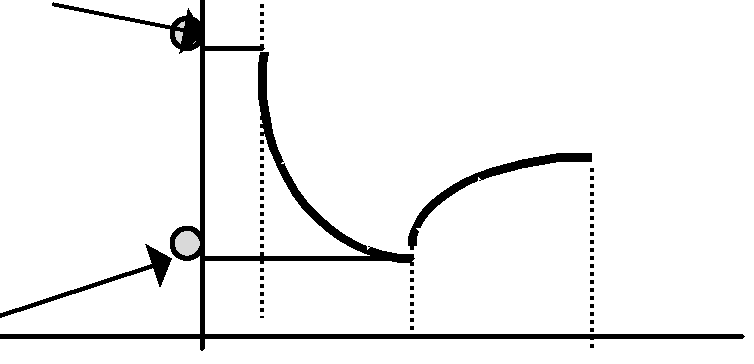
(г) Если f(x)=0  {a_i-корни функции;i=1,2,…}, на каждом из промежутков (a_i; a_i+1) функция "сохраняет знак". Это свойство непрерывной функции лежит в основе "метода интервалов" решения неравенств: для построения "знаковой картинки" достаточно с помощью любой "пробной точки" x(a_i; a_i+1) определить "знак" функции на интервале (a_i; a_i+1).

3) Определение. Число "х₀"R называется корнем функции f , если f(x₀)=0. Очевидно, что корень функции является точкой пересечения графика функции y=f(x) c осью абсцисс.

Теорема Больцано - Коши (существование корня функции).

Если функция, непрерывная на замкнутом промежутке [a,b], принимает на его концах значения "разного знака" , внутри промежутка (a,b) существует по крайней мере один корень функции

На этом свойстве непрерывной функции, имеющей на промежутке (а,b) единственный корень, основан "Метод половинного деления" уточнения корня с заданной погрешностью ps.

Алгоритм метода :

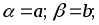1. (2)

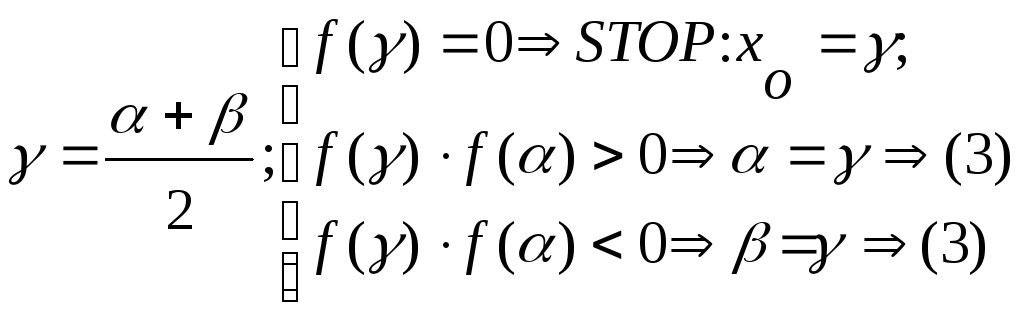
(3)если с заданной погрешностью ps;

иначе  перейти к п^о2.

Замечание. Для уточнения корня функции на промежутке [a,b] с заданной погрешностью необходимо выполнить