
- •3.5. Приемы гармонизации композиции
- •3.6. Цвет в композиции костюма
- •3.7. Фактура в композиции костюма
- •3.8. Основы графического моделирования на начальном этапе изучения композиции
- •3.8.1. Типы проектно-графического изображения
- •Глава 3
- •Костюма
- •3.1. Определение композиции
- •3.2. Композиционное формообразование
- •3.3. Целостность композиции
- •3.4. Средства композиции
- •Глава 5 основы проектирования одежды
- •5.1. Основные этапы проектирования
- •5.2. Творческая концепция в дизайне одежды
- •Глава 7
- •7.1. Идейно-творческие основы дизайна
- •7.2. Этапы художественного творчества
- •Костюма практикум
- •Глава 4
- •4.1. Линейная графика
- •5.1. Стиль и стилизация. Основные понятия
- •7.3. Стилизация фигуры. Индивидуальный стиль
- •8.1. Пропорциональные соотношения фигуры человека и его одежды
- •8.2. Выявление пропорциональных соотношений силуэта
- •Глава 19
- •19.1. Унисекс
- •19.2. Заимствования из мужского гардероба
- •Спецрисунок и художественная графика
- •Живописи. Упражнения для работы акварелью
8.1. Пропорциональные соотношения фигуры человека и его одежды
Мы познаем мир, сравнивая и сопоставляя
разные явления, предметы, формы и качества. Оценивая одежду, сравнивая, как соотносится верхняя часть костюма с нижней, мы сравниваем их размер, цвет, фактуру, массу. Соотношение этих величин, не вызывающее дисгармонии при визуальном восприятии, свидетельствует об их согласованности, соразмерности.
Пропорциональные соотношения — это количественные соотношения, соразмерность частей, составляющих целое.
Простейший вид согласованности — это тождество, или равенство, сравниваемых величин. Нюансное соотношение представляет собой незначительное различие при сравнении. Контрастное соотношение — это противопоставление при сравнении формы, цвета, площади и т.д.
В проектировании одежды при помощи пропорционирования организуется форма костюма и достигается ее гармоничное восприятие. Арифметические пропорции основаны на равенстве между двумя отношениями четырех величин, например: а:Ь = с:с1. Они содержат в себе модуль, который можно уложить целое число раз в каждой части. В организации костюма используют отношения целых чисел до 8, так как костюм воспринимается в единой системе с фигурой человека.
Геометрические пропорции основаны на геометрической закономерности их построения (например, отношение стороны прямоугольника к его диагонали). Наиболее известное пропорциональное отношение, выражающее гармоничное соотношение целого и его частей, — золотое сечение, т.е. деление отрезка на две неравные части таким образом, что большая его часть относится к меньшей, как весь отрезок к большей. Термин «золотое сечение» ввел Леонардо да Винчи, в целых числах оно выражается как 5:3, 8:5, 13:8 и т.д. Этот принцип был заложен в архитектуре и искусстве античной Греции.
В дальнейшем на пропорциональные отношения в одежде стали оказывать модные тенденции, предлагающие новые пропорциональные членения костюма. Это привело к появлению рукава 3/4, пальто 7/8> мини-юбки '/з-
66
8.2. Выявление пропорциональных соотношений силуэта
Для гармоничного восприятия человека и
костюма как единого целого членение одежды не должно противоречить пропорциям фигуры человека. При проектировании одежды система пропорциональных соотношений частей костюма накладывается на пропорции фигуры человека. При этом следует помнить о количественном соотношении силуэта костюма и фигуры.
Дизайн рассматривает любую вещь с точки зрения гармоничного сочетания ее функции и красоты. Иными словами, костюм, в котором неудобно двигаться, который не соответствует своему назначению, не может быть красивым с точки зрения дизайна. Эрганомичный подход к дизайну одежды выражается в выборе композиционных, конструктивных и технологических решений, позволяющих добиться результата, при котором одежда будет максимально соответствовать пропорциям тела человека.
Пропорциональные соотношения в одежде зависят от модных тенденций. Длина юбки и расположение линии талии в течение долгого времени определяли модный силуэт. Несмотря на то что
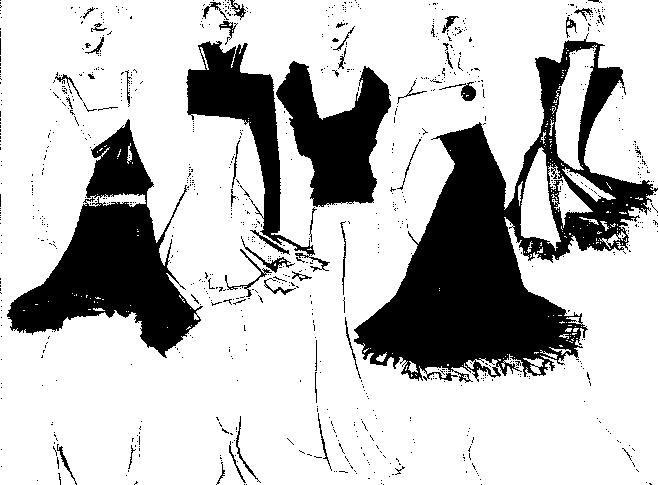
'Рис. 8.1. Пропорциональные соотношения внутри силуэта. Логический ряд.
Студенческая работа
67
