15.4. Дифференциальные уравнения переноса массы

Для вывода уравнений конвективного переноса массы восполь­зуемся основным уравнением переноса субстанций [уравнение (3.27)]:

где φ-потенциал переноса массы; q-плотность потока массы; у-источник переноса массы (принимаем, что у = 0, так как дополнительный подвод массы к потоку отсутствует).

В процессах массопередачи потенциалом переноса является концентрация, и поэтому

Плотность потока массы q складывается из двух составляющих:

В уравнении (15.24) величина отражает плот­ность молекулярного переноса массы [первый закон Фика, уравне­ние (3.14)], -плотность конвективного потока массы.

Тогда основное уравнение переноса субстанции применительно к процессу переноса массы запишется следующим образом:

(15.25)

Причем

Поскольку при условии неразрывности потока величина то уравнение (15.25) принимает вид

(15.27)

В уравнении (15.25) значение divgradc выражается как

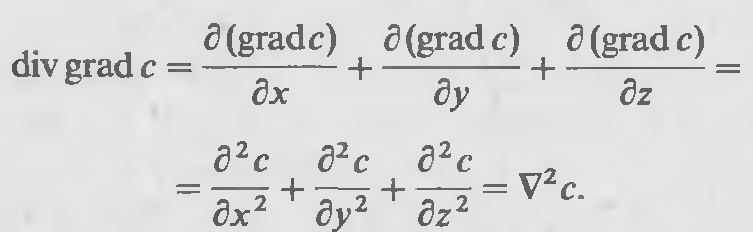
Таким образом, после проведенных преобразований уравнение (15.25) обращается в дифференциальное уравнение (3.46) конвек­тивной диффузии:

которое выражает в общем виде распределение концентрации компонента в движущемся потоке при неустановившемся процессе массопереноса.

При массопереносе в неподвижной среде W_х = W_у = W_г = 0, и уравнение (3.46) примет следующий вид:

(15.29)

Уравнение (15.29) называют дифференциальным уравнением мо­лекулярной диффузии, или вторым законом Фика. Оно описывает распределение концентраций вещества в неподвижной среде моле­кулярной диффузией.

Отметим, что уравнение конвективной диффузии, поскольку процесс переноса массы протекает в потоке, должно было допол­нено уравнениями движения Навье-Стокса и неразрывности по­тока. Кроме того, перенос вещества приводит к изменению состава фаз и, следовательно, к изменению их физических свойств. Поэтому систему дифференциальных уравнений, описывающих конвектив­ный массоперенос, следует дополнить также уравнениями, отра­жающими зависимость физических свойств фазы от ее состава. Расчет такой системы уравнений представляет большие трудности, и аналитическое решение этой системы уравнений оказывается практически целесообразным только в тех случаях, когда возможны существенные ее упрощения. Поэтому часто для решения этой задачи используют методы теории подобия.

15.5. Подобие массообменных процессов

Общность дифференциальных уравнений теплообмена (3.40) и массообмена (15.25) позволяет полагать, что основные критерии массообменных процессов должны быть аналогичны основным критериям теплообмена.

Рассмотрим' уравнения массопереноса на границе раздела фаз. Из одной фазы в другую переходит количество массы, равное

где -равновесная концентрация на границе раздела фаз.

Это же количество массы переносится молекулярной диффузией через пограничный слой:

В этих уравнениях трудноопределимы величины -_ и n-тол­щина пограничного слоя, через который проходит вещество моле­кулярной диффузией. Отсюда

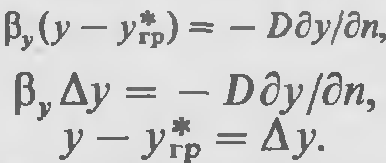
Перемножим на масштабные множители каждый член послед­него уравнения:

Тогда

Откуда

где l-определяющий геометрический размер.

Данный безразмерный комплекс является аналогом теплового критерия Нуссельта (Nu = аl/λ) и называется поэтому диффузион­ным критерием Нуссельта (иногда-критерием Шервуда Sh). Кри­терий Нуссельта Nu является определяемым критерием, поскольку в него входит величина β. Так как Nu ~ β/D), то Nu характеризует отношение скорости переноса вещества (конвективного и молеку­лярного -β) к молекулярному переносу (D).

Другие критерии массообменных процессов получим из диф­ференциального уравнения конвективной диффузии (15.25). Пере­писав уравнение (15.25) относительно оси х:

и проведя его подобное преобразование, получим следующие кри­терии подобия:

-диффузионный критерий Фурье (аналог теплового критерия Фурье который характеризует подобие не- установившихся процессов массообмена;

Wl/D = Ре'-диффузионный критерий Пекле (аналог теплового критерия Пекле Р = Wl/а).

Критерий Ре' ~ W/D характеризует отношение переноса ве­щества кон векцией (W) к молекулярному переносу (D) в сходст­венных точках подобных систем. Часто критерий Ре' заменяют отношением

Диффузионный критерий Прандтля Рr' является аналогом теп­лового критерия Рг = V/а (иногда критерий Рr' называют критерием Шмидта Sс).

Формально критерий Рr' выражает постоянство отношения фи­зических свойств жидкости или газа в сходственных точках подоб­ных систем. По существу же критерий Рr' характеризует отношение профиля скоростей (через V) к профилю концентраций (через D ), т. е. отношение толщины гидродинамического и диффузионного погра­ничных слоев.

Для соблюдения подобия процессов массоотдачи необходимо также соблюдение гидродинамического подобия. Поэтому крите­риальное уравнение массоотдачи для неустановившегося процесса будет иметь следующий вид (Г-геометрический симплекс-см. гл. 5):

При установившемся процессе и при отсутствии влияния сил тяжести (т. е. при Fо' = 0 и Gа = 0):

например

(15.30)

где А, n, m, q, р определяют опытным путем.

Уравнение (15.30) является обобщенным критериальным урав­нением массоотдачи. Поскольку оно аналогично критериальному уравнению теплоотдачи (11.35,а), то при одинаковых гидродина­мических условиях

(15 31)

С помощью выражения (15.31) можно найти соотношение между коэффициентами тепло- и массоотдачи:

(15.31а)

которое позволяет по известному значению, например а, опреде­лить величину коэффициента массоотдачи β при одних и тех же гидродинамических условиях.