9. Граф оптимальных путей

В соответствии с приведенным решением видно, что потоки φ_1-4, φ_5-2

передаются по оптимальным путям. Можем составить следующий граф:

Рисунок 4. Графическое представление оптимального решения задачи

В результате решения получили следующие значения для потоков:

Х1=0; Х2=33; Х3=68; Х4=0; Х5=0; Х6=0.

Из полученного решения следует, что пропускные способности некоторых путей используются не полностью для передачи двух потоков информации. В результате возникают скрытые запасы соответствующих пропускных способностей, величины которых определяются значением дополнительных переменных Y4=56, Y5=14, Y6=1, Y7=20 и Y8=15 в оптимальном решении прямой задачи.

10. Параметрический анализ

Под параметрическим анализом будем понимать решение задачи оптимизации при различных значе­ниях того параметра, который ограничивает улучшение целе­вой функции.

Приведем данную задачу и её решение на Excel. Опираясь на условия задачи, введем исходные данные в форму, а также необходимые формулы для расчета левой части и целевой функции, эти данные представлены на рисунке 5.

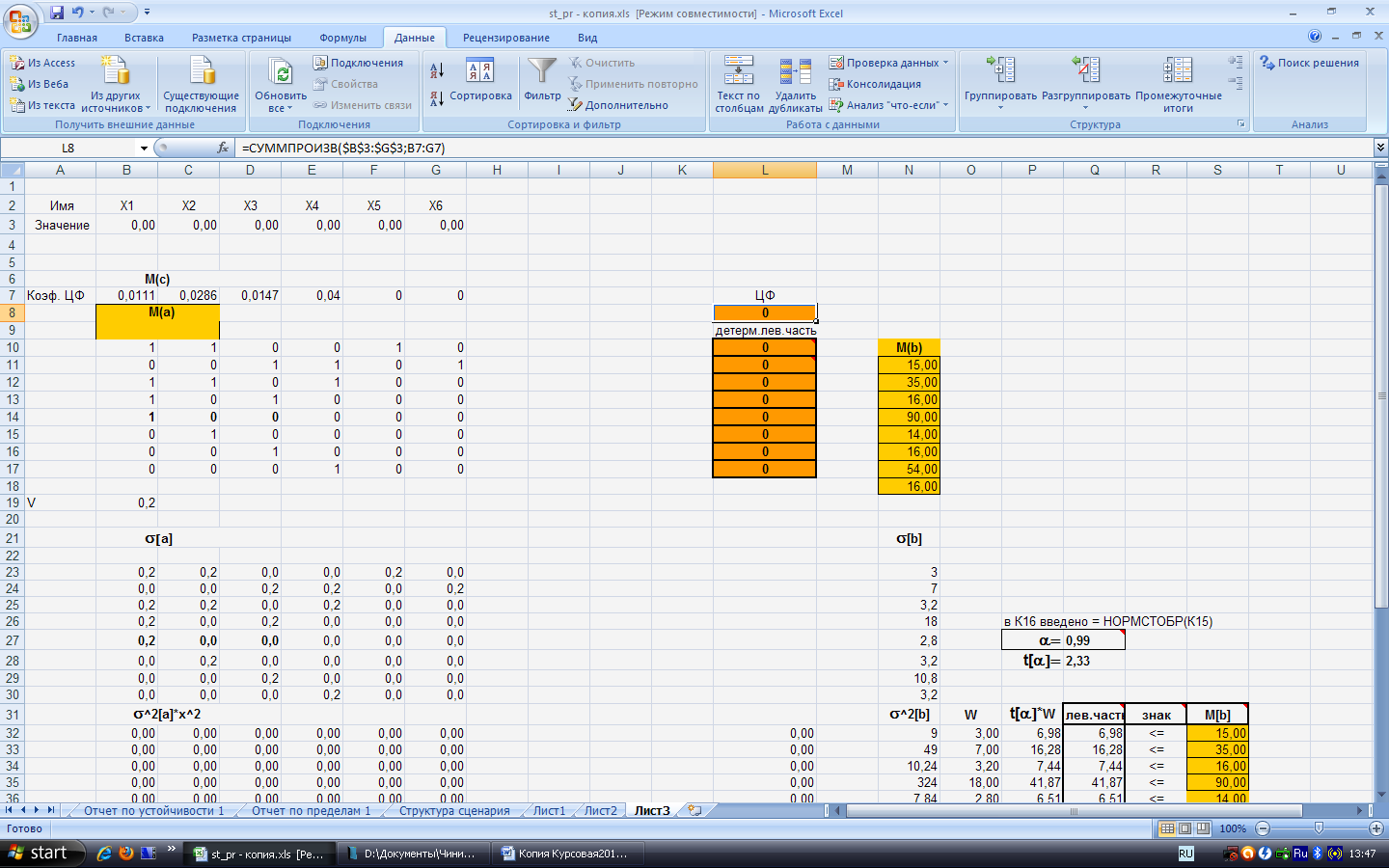
Рисунок 5 – Формула для расчета целевой функции

После этого заходим в меню СЕРВИС, ПОИСК РЕШЕНИЯ. На экране появляется окно представленное на рисунке 6.

Рисунок 6 – Окно «Поиск решения»

В окне «Поиск решения» устанавливаем целевую ячейку L8. Выбираем направление целевой функции равной: Максимальному значению. Добавляем необходимые ограничения, нажимаем кнопку ВЫПОЛНИТЬ и получаем результат решения представленный на рисунке 7.

Рисунок 7 – Результат поиска решения

В Excel анализ оптимального решения можно осуществить, пользуясь различными отчётами. Так отчёт по устойчивости представлен на рисунке 8.

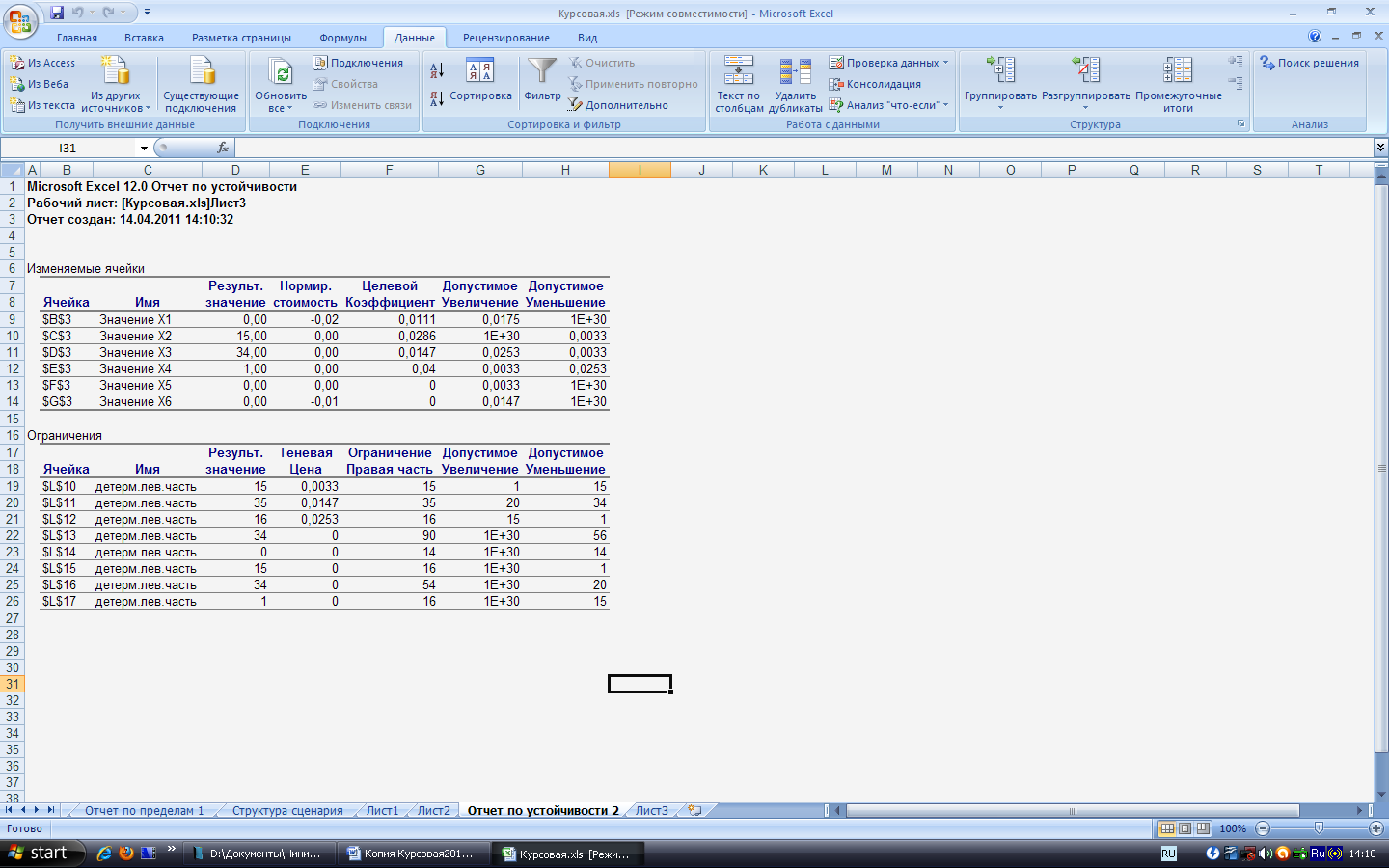
Рисунок 8 – Отчёт по устойчивости

Отчёт по результатам представлен на рисунке 9.

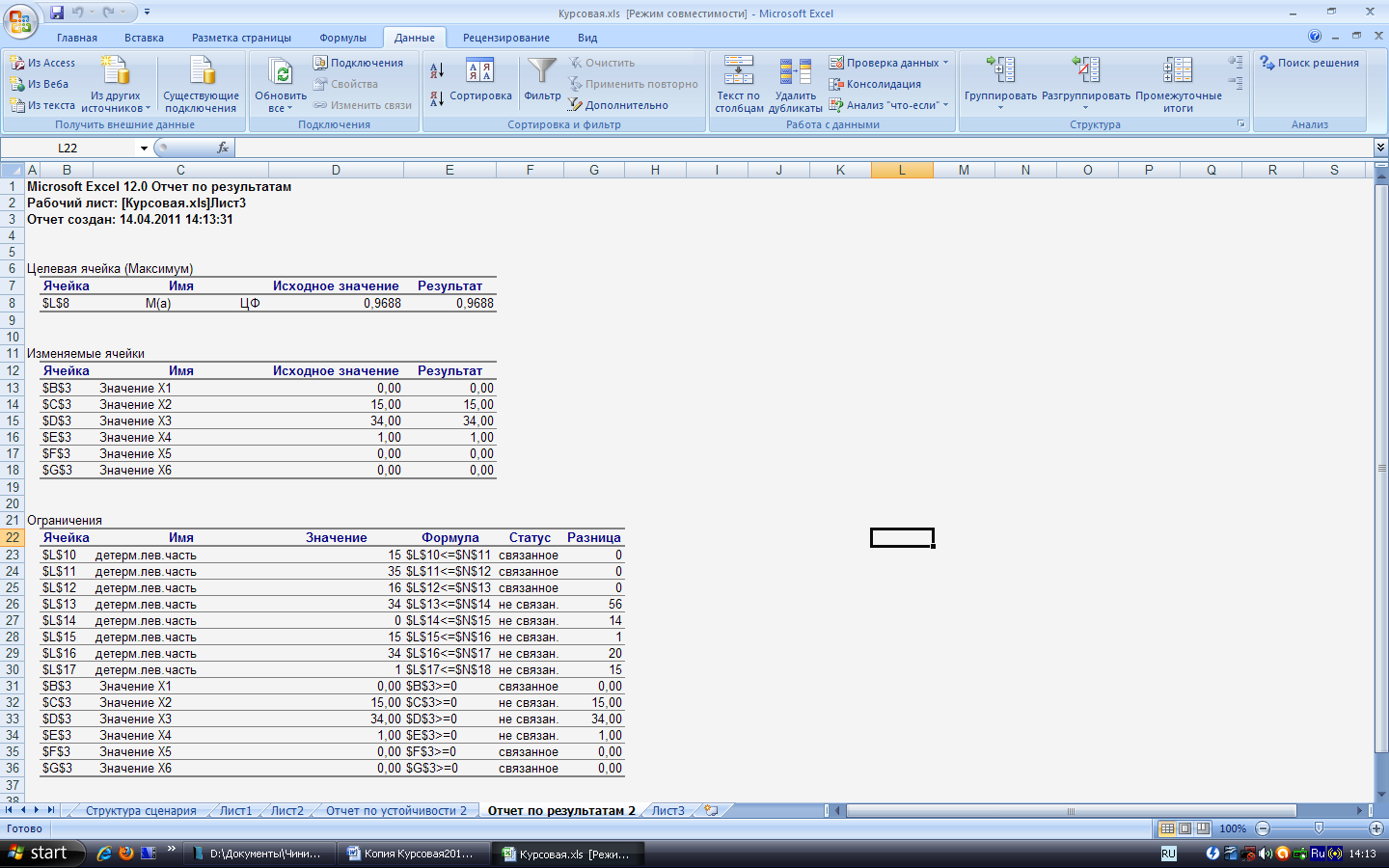
Рисунок 9 – Отчет по результатам

Таблица «Целевая ячейка» приводит сведения о целевой функции. В столбце «Исходное значение» приведены значения целевой функции до начала вычислений.

Таблица «Изменяемые ячейки» приводит значения искомых переменных, полученных в результате решения задачи;

Таблица «Ограничения» показывает результаты оптимального решения для ограничений и для граничных условий.

В графе «Значение» приведены величины использованной пропускной способности; в графе Разница показано количество неиспользованного ресурса ветви сети. Если пропускная способность используется полностью, то в графе «Состояние» указывается связанное; при неполном использовании – не связанное.

Для граничных условий приводятся аналогичные величины с той лишь разницей, что вместо величины неиспользованного ресурса ветви сети показана разность между значением переменной в найденном оптимальном решении и заданным для нее условием.

Отчёт по пределам представлен на рисунке 10. В нем показано, в каких пределах может изменяться объем передаваемой информации, вошедший в оптимальное решение, при сохранении структуры оптимального решения.

Рисунок 10 – Отчет по пределам

В отчете указаны значения целевой функции при передаче данного вида информации на нижнем пределе. Далее приводятся верхние пределы изменения x_j и значения целевой функции при передаче информации, вошедшей в опти­мальное решение на верхних пределах.

Рассмотрим ситуацию при введении помехи. Примем математическое ожидание М(b)=100, а среднеквадратичное отклонение σ(b)=20.

В результате получим коэффициент вариабельности V= σ(b) / М(b)=0,2.

C учетом этого коэффициента пересчитаем матрицу левых коэффициентов М(а) и получим матрицу отклонений данных коэффициентов σ(а)= М(а)*V (рис.11).

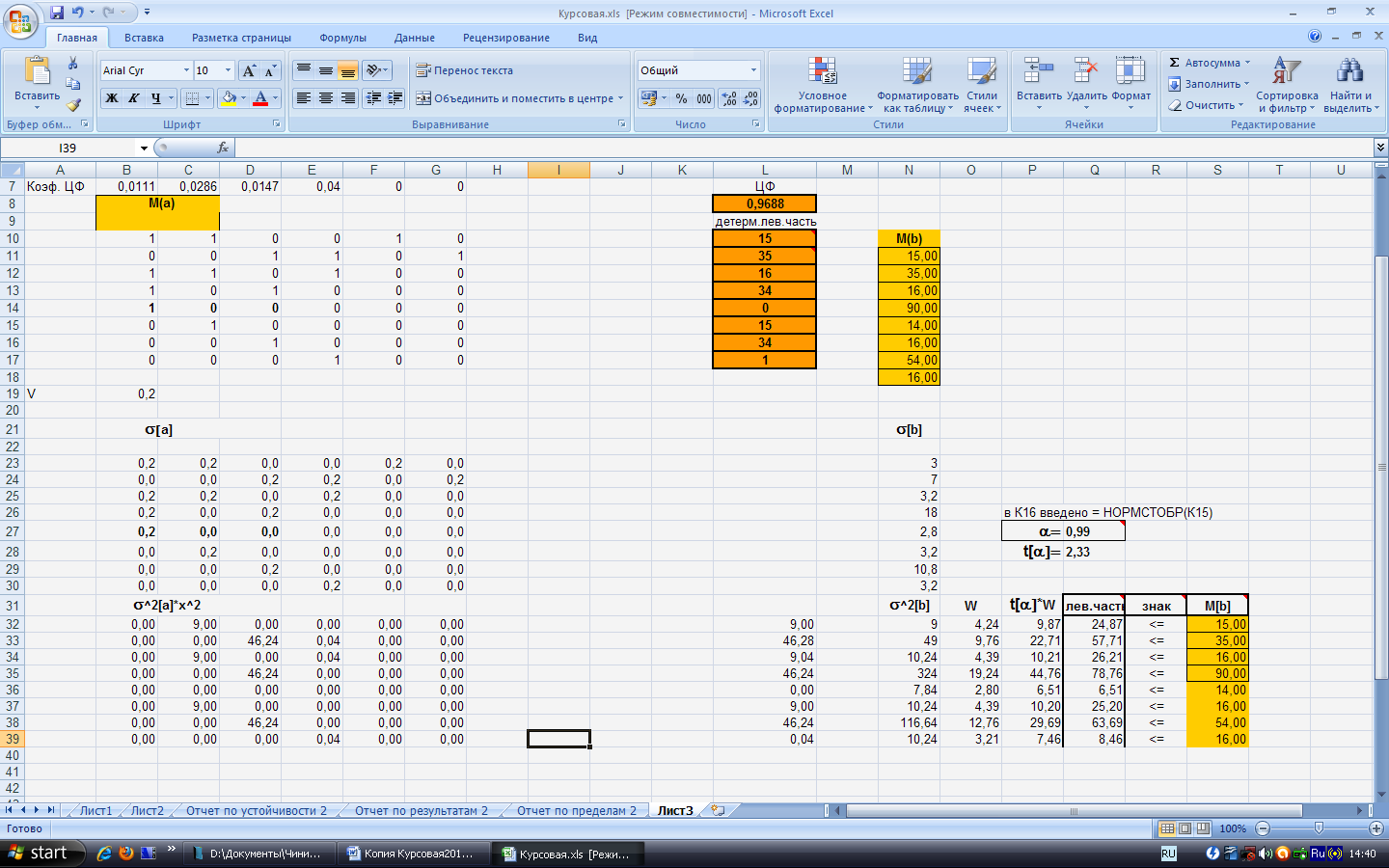
Рисунок 11 – Матрица σ(а)

Затем находим матрицу σ²(а)*Х² (рис. 12)

Рисунок 12 - Матрица σ²(а)*Х²

Пересчитав столбец правых частей ограничений M(b) с учетом коэффициента вариабельности V=0,2 получим σ(b) и σ²(b) (рис.13)

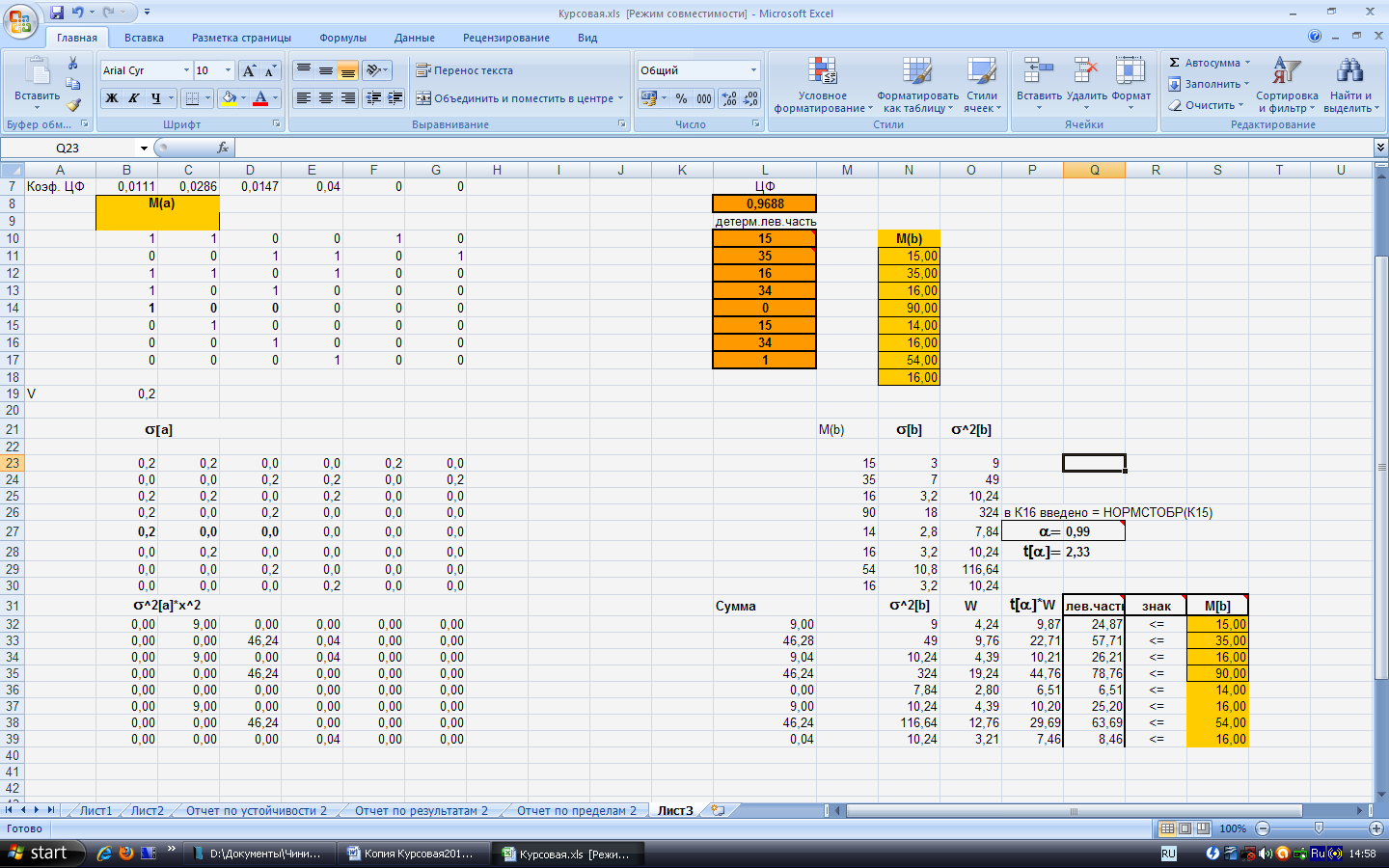
Рисунок 13 – Отклонение и среднеквадратичное отклонение

Введем вероятность, с которой должно быть выполнено ограничение α=0,99.

Рассчитали обратное значение нормального распределения при α=0,99 t(α)=2,33. В результате получим:

Проведем параметрический анализ при V=0.

Варианты изменения третьей оценки представлены на рис. 14.

Рисунок 14 – варианты изменения оценки

Исходные варианты подставим в правую часть третьего ограничения. Полученные значения сохраним в отдельных сценариях (b3=16, b3=20, b3=24) и занесем их в таблицу 12.

Таблица 12 – Значения целевой функции

Вариант	1	2	3
Поток	16	20	24
ЦФ	0,9688	1,07	1,1712

В результате получим итоговый сценарий, который представлен

на рисунке 15.

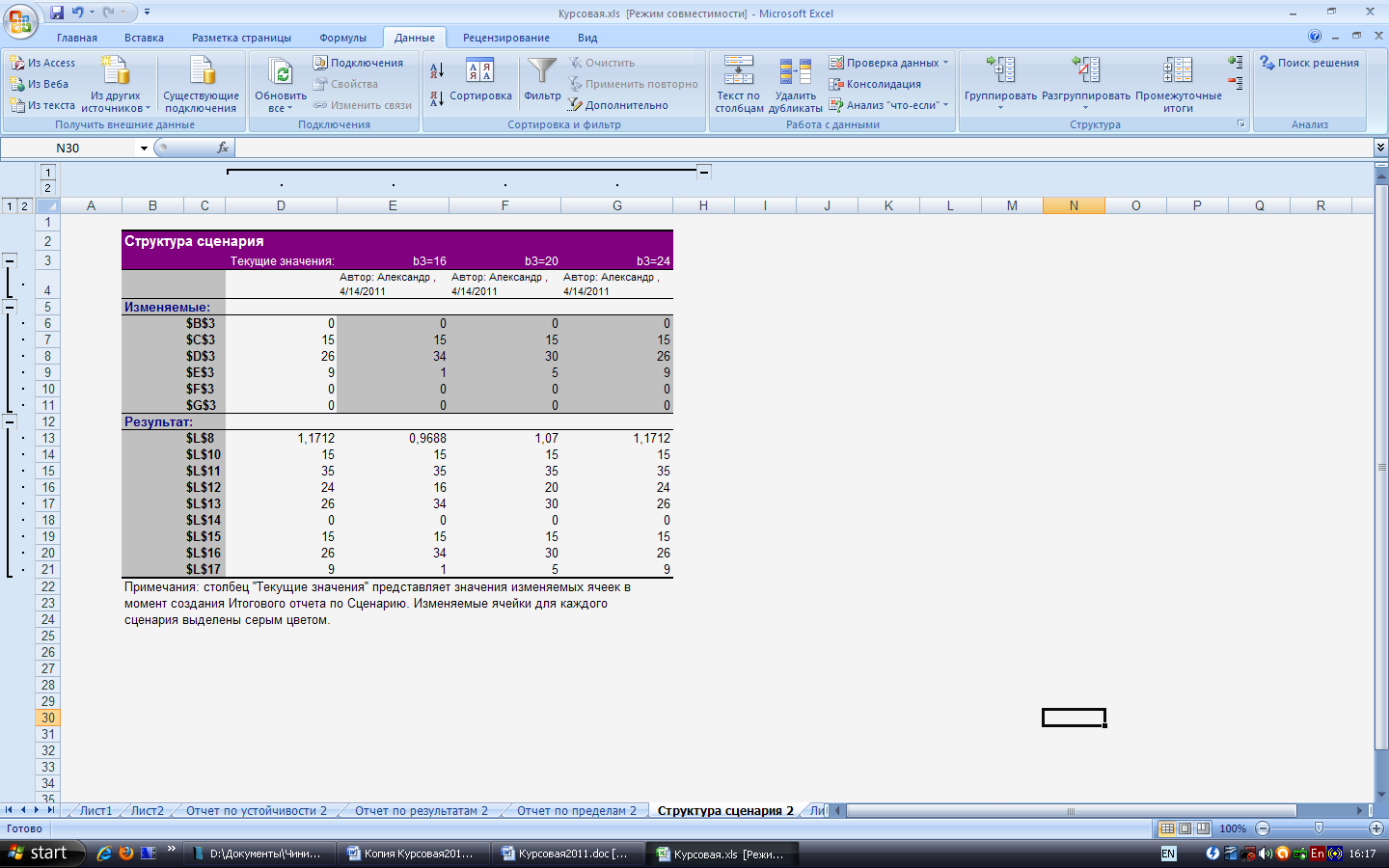
Рисунок 15 – Итоговый сценарий

Для наглядного представления результатов параметрического анализа на основании отредактированной таблицы итогового сценария построим график. Построим гистограмму для целевой функции путей связи, гистограммы изображены на рисунке 16.

Рисунок 16 – Стоимость передачи при различных значениях потока

Из данной гистограммы видно, что полезность пути тем выше, чем больше информации передается, т.е. для наиболее оптимального плана передачи необходимо полностью использовать пропускные способности сетей связи.