6. Экономическая интерпретация двойственности

Полученные значения переменных двойственной задачи: Y1*=0,03; Y2*=0 и Y3*=0,03 показывают, насколько изменится целевая функция прямой задачи при изменении на единицу полезности соответственно первой и третьей ветвей. Значения Y4*=0; Y5*=0; Y6*=0; Y7*=0 и Y8*=0 свидетельствуют о том, что изменение данного вида ресурса (пропускных способностей соответствующих путей) не приводит к изменению целевой функции. Это свидетельствует о том, что данный ресурс использован не полностью для получения оптимального решения, т.е. имеет место скрытый запас этого вида ресурса. Величина скрытого запаса определяется значением дополнительных переменных Y4=56; Y5=14; Y6=1; Y7=20; Y8=15 в оптимальном решении прямой задачи. Таким образом, положительную, отличную от нуля двойственную оценку имеют те ресурсы, которые полностью используются при оптимальном плане передачи информации, поэтому двойственные оценки определяют дефицитность используемых ресурсов (полезность путей). Левые части ограничений двойственной задачи определяют стоимость каждого пути.

Если в рассматриваемой задаче подставить полученные значения Y1* и Y3* двойственной задачи в ограничения, то имеют место соотношения:

0,06>0,01;

0,03=0,03;

0,01=0,01;

0,06>0,04;

0,03>0;

0.03>0.

Первое , четвертое, пятое, шестое ограничения двойственной задачи в соотношении выполняются, как строгие неравенства. Это означает, что помехозащищенность этих ветвей оказалась ниже, т.е. передача информации по этим путям нерентабельна, и, как следует из решения прямой задачи, путь четвёртый не предусмотрен сетью (Х4=0). Его необходимо использовать из-за отсутствия других вариантов.

Второе и третье ограничения в соотношении выполняются как строгие равенства. Это означает, что двойственная оценка полезности соответствующих путей в точности соответствует их ценам. Отсюда следует, что передача информации по первому и третьему пути экономически целесообразна и предусмотрена графом путей (Х1=15; Х3=35).

Целевая функция двойственной задачи показывает общую оценку путей, используемых при передаче информации, и она должна быть минимальной.

7. Исследование чувствительности решения к изменению правых частей ограничений

Анализ чувствительности полученного решения прямой задачи к изменению коэффициентов Вi предполагает, что вычисляются пределы изменения каждого из коэффициентов, при которых опорное решение прямой задачи существует или оптимальное значение переменных двойственной задачи Yi* постоянно.

Решение прямой задачи можно записать через матрицу перехода для конечной симплекс-таблицы в виде:

(*),

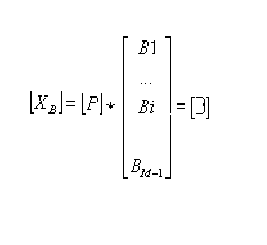[X_В] – столбец базисных переменных конечной симплекс-таблицы;

[P] – матрица переход;

[B₁, …, B_i, …, B_M-1]^T - матрица-столбец свободных членов исходной симплекс таблицы;

[B] – матрица-столбец свободных членов конечной симплекс-таблицы;

Для оценки пределов изменения правых частей ограничений и коэффициентов целевой функции достаточно информации, содержащейся в конечной симплекс-таблице. Для любой итерации симплекс-метода значения базисных переменных могут быть вычислены с помощью матрицы перехода [P]. Матрица перехода [P] формируется из коэффициентов симплекс-таблицы для данной итерации. Это квадратная матрица размерностью (М-1)х(М-1) для прямой задачи и (N-1)x(N-1) – для двойственной. Столбцы матрицы соответствуют дополнительным переменным прямой задачи или дополнительным переменным двойственной задачи и располагаются в прямом порядке Y1,Y2, ... ,YM-1 или X1*,X2*, … ,XN-1*. Если дополнительные переменные Yi (или Xj*) для прямой или двойственной задачи на данной итерации являются базисными переменными, то соответствующие им столбцы матрицы перехода [P] состоят из нулей во всех строках, кроме одной, в которой присутствует единица. Номера этих строк совпадают с номерами строк, в которых находятся эти переменные в столбце базисных переменных. Столбцы матрицы перехода [P] для дополнительных переменных Yi (или Xj*), которые для рассматриваемой итерации являются свободными, соответствуют столбцам симплекс-таблицы для данной итерации для этих же переменных. Используя соотношение (*) для конечной симплекс-таблицы прямой задачи и задавая приращения исходным значениям правых частей ограничений Вi+∆Вi можно найти величины этих приращений. Вектор устойчивости опорного решения можно записать в виде:

где [P] – матрица перехода для конечной симплекс-таблицы.

Так как

то вектор устойчивости опорного решения можно записать следующим образом:

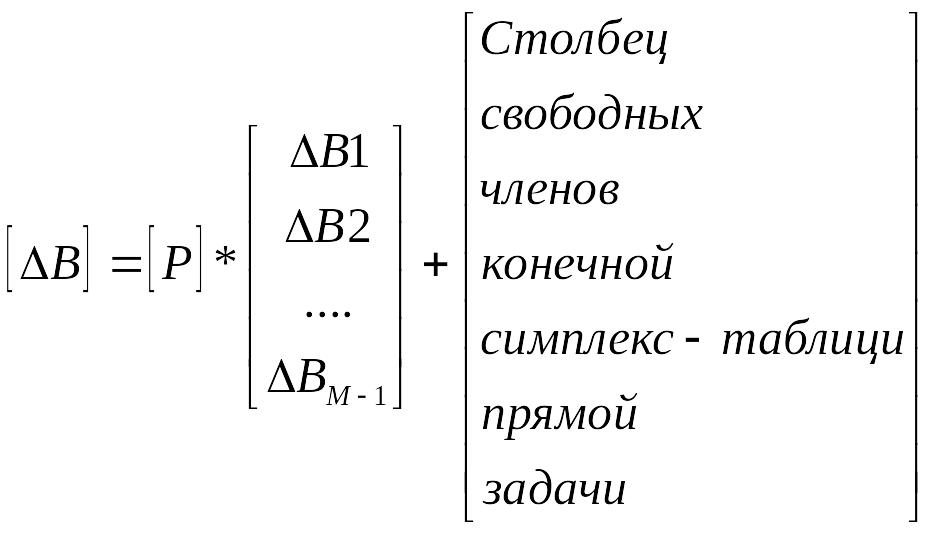
Составим матрицу перехода для конечной симплекс-таблицы прямой задачи, опираясь на выше изложенные правила:

Условие не отрицательности компонент вектора [∆B] приводит к системе неравенств:

1 5 + ∆B1  0;

15 + ∆B1+35+ ∆B2 – 16 - ∆B3 0;

- 15 - ∆B1+16+∆B3  0;

- 15 - ∆B1 – 35 - ∆B2+16+∆B3+90+∆B4  0;

14 +∆B5  0;

- 15 - ∆B1 – 35 - ∆B2+16+∆B3+16+∆B6  0;

- 15 - ∆B1 – 35 - ∆B2+16+∆B3+54+∆B7  0;

- 15 - ∆B1+16+∆B3+16+∆B8  0.

Свободные члены данной системы неравенств повторяют столбец свободных членов конечной симплекс-таблицы прямой задачи.

Анализ всех коэффициентов одновременно затруднителен и требует решения сложных систем неравенств. Будем рассматривать изменение только одного коэффициента, например ∆B1, и тогда ∆B10, а остальные ∆Bi=0, i=2, М-1, при таких условиях решается система неравенств для определения допустимых пределов изменения ∆B1. Аналогично исследуются пределы изменения остальных коэффициентов ∆Bi.Для определения пределов изменения целевой функции F прямой задачи, при соответствующих приращениях ∆Bi, используется полученное значение переменных двойственной задачи Yi*. Ранее установили, что каждому i-ому ограничению прямой задачи соответствуют переменные двойственной задачи. Если двойственная переменная Yi* в последней симплекс – таблице двойственной задачи находится в числе свободных и, следовательно, Yi*=С, то приращение целевой функции определяется как ∆F= Yi*∆Bi. Если Yi* находится в числе базисных переменных последней симплекс – таблицы и вычислены допустимые пределы изменения коэффициентов ∆Bi, то есть ∆Bi_min≤∆Bi≤∆Bi_max, то пределы изменения будут ∆Bi_min Yi* ≤∆F≤∆Bi_max Yi*.

Вычислим коэффициенты неравенств для решаемой задачи:

	-X1	-Y1	-Y2	-Y3	-X5	-X6	B
X2	1	1	0	0	1	0	15
Х3	0	1	1	-1	1	1	34
X4	0	-1	0	1	-1	0	1
Y4	1	-1	-1	1	-1	-1	56
Y5	1	0	0	0	0	0	14
Y6	0	-1	-1	1	-1	-1	1
Y7	0	-1	-1	1	-1	-1	20
Y8	0	1	0	-1	1	0	15
Fmax	0,02	0	0,01	0,03	0	0,01	0,97

1) Пусть ∆B10, ∆Bi=0, i=2…8, тогда получим систему неравенств:

∆B1  -15;

∆B1  -34;

∆B1 ≤ 1;

∆B1 ≤ 56;

∆B1 ≤ -18;

∆B1 ≤ 20;

∆B1 ≤ 17.

отсюда следует, что ∆B2:

-34 ≤ ∆B2 ≤ 56

так как Y1*=0, то изменение значений целевой функции при этом будет равно: ∆F_max=0.

2) Пусть ∆B20, ∆Bi=0, i=1,3…8, тогда получим систему неравенств:

∆B2  -34;

∆B2 ≤ 56;

∆B2 ≤ -18;

∆B2 ≤ 20

отсюда следует, что ∆B2:

-34 ≤ ∆B1 ≤ 56, т.е. изменение значений целевой функции будет происходить в пределах ∆B2_min Y2* ≤ ∆F_max≤∆B1_max Y2*, т.е.:

-1,02 ≤ ∆F_max ≤ 1,68.

3) Пусть ∆B30, ∆Bi=0, i=1,2,4…8, тогда получим систему неравенств:

∆B3  -1;

∆B3  -56;

∆B3  18;

∆B3  -20;

∆B3 ≤ 34;

∆B3  -17

отсюда следует, что ∆B3:

-56 ≤ ∆B3 ≤ 34, т.е. изменение значений целевой функции будет происходить в пределах ∆B3_min Y3* ≤ ∆F_max≤∆B3_max Y3*, т.е.:

-1,68 ≤ ∆F_max ≤ 1,02.

4) Пусть ∆B40, ∆Bi=0, i=1..3,5…8, тогда получим систему неравенств:

∆B4  -56;

так как Y4*=0, то изменение значений целевой функции при этом будет равно: ∆F_max=0.

5) Пусть ∆B50, ∆Bi=0, i=1..4,6…8, тогда получим систему неравенств:

∆B5  -14;

так как Y5*=0, то изменение значений целевой функции при этом будет равно: ∆F_max=0.

6) Пусть ∆B60, ∆Bi=0, i=1..5,7…8, тогда получим систему неравенств:

∆B6  -18;

так как Y6*=0, то изменение значений целевой функции при этом будет равно: ∆F_max=0.

7) Пусть ∆B70, ∆Bi=0, i=1..6,8, тогда получим систему неравенств:

∆B7  -20;

так как Y7*=0, то изменение значений целевой функции при этом будет равно: ∆F_max=0.

8) Пусть ∆B80, ∆Bi=0, i=1..7, тогда получим систему неравенств:

∆B8  -17;

так как Y8*=0, то изменение значений целевой функции при этом будет равно: ∆F_max=0.

Пусть ∆B20, ∆B30 ∆Bi=0, i=1,4..8, тогда получим систему неравенств:

- 34 ≤ ∆B1 ≤ 56;

-56 ≤ ∆B3 ≤ 34.

Графически решение данной системы можно представить следующим образом:

∆B3

Рисунок 2. Графическое решение системы

Изменение значений целевой функции будет происходить в пределах

-1,68 ≤ ∆F_max ≤ 1,02.

Возьмем, для примера, из найденной области точку с координатами ∆B2=-10, ∆B3=20. Произведем решение задачи с новыми значениями В2=5 и В3=14

Таблица 9. Конечная симплекс-таблица двойственной задачи:

	-X2*	-X4*	-X3*	-Y4*	-Y5*	-Y6*	-Y7*	-Y8*	B
Y1*	-1	0	1	-1	0	0	0	0	0,03
X1*	-1	0	1	0	0	0	1	0	0,06
Y2*	0	-1	0	0	1	-1	0	0	0
Y3*	0	-1	0	0	1	0	0	1	0,03
X5*	-1	0	1	0	0	0	1	0	0,06
X6*	0	-1	0	0	0	0	0	0	0,03
Фmin	5	3	14	36	12	1	25	20	-0,87

Значение рабочей точки не изменилось: Y1*=0,03 и Y3*=0,03.