Лемма Неймана-Пирсона

Рассмотрим вероятностную модель состоящую из двух распределений Р₀ Р₁ с общим носителем и функциями плотности и , . По выборке проверяется простая гипотеза Н₀ : выборка взята из распределения Р₀ при простой альтернативе Н₁ : выборке соответствует распределение Р₁. Определим критическую функцию как индикаторную функцию критической области.

Статистика L называется статистикой отношения правдоподобия, а критерий - критерием отношения правдоподобия или критерием Неймана-Пирсона.

Критерий отвергает нулевую гипотезу, если правдоподобие альтернативы функции в С раз превосходит правдоподобие нулевой гипотезы . Этот критерий обладает следующими замечательными свойствами.

Теорема 8.1. Критерий отношения правдоподобия является наиболее мощным критерием в классе всех критериев проверки простой гипотезы при простой альтернативе, размер которых не превосходит размера критерия . Если критерий имеет размер , то он обладает наибольшей мощностью в классе всех критериев уровня .

Доказательство

Пусть - любой другой критерий, размер которого

. (1)

Требуется показать, что тогда критерий имеет большую мощность чем критерий , то есть .

Рассмотрим интеграл .

Достаточно показать, что этот интеграл не отрицательный, и тогда первое утверждение теоремы будет следовать из неравенства:

, которая влечет (см. (1))

.

Покажем , что функции и произведение которых интегрируется., одновременно положительны или отрицательны при любых . Действительно, если , то это влечет , поскольку критическая функция равна единице, если она не равна нулю. Но по определению критерия отношения правдоподобия, равенство возможно лишь в случае когда . Точно так же устанавливается, что неравенство влечет .

И так , критерий наиболее мощен в классе всех критериев, размер которых не превосходит размера . Если же , то это утверждение очевидно влечет его наибольшую мощность в классе всех критериев уровня .

Пример. Нормальное распределение. , ,

Мат. ожидания одинаковы и равны нулю.

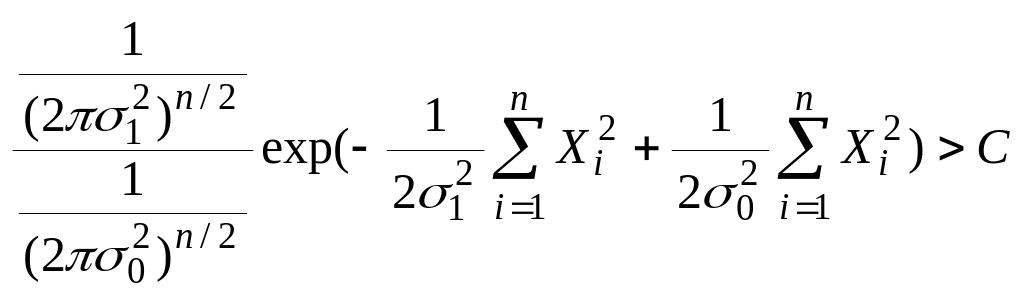
Это неравенство соответствует следующему, исходя из предположения, что (в противном случае знак неравенства нужно менять)

Если вектор попал в сферу радиуса , то принимаем гипотезу

Х_i получены распределением

Если , то

(Хи квадрат с n-степенями свободы)

Плотность распределения x2n

Зная находим в таблице распределения _т² Кn()

- ошибка первого рода.

- ошибка второго рода.

В этих двух примерах нам не нужна была сама выборка , а только функция от нее ( )

Пример. Биномиальное распределение.

-вероятность получить выборку если было использовано распределение

0,1 вероятность получить этот вектор для , q₁ число нулей, p₁ число единиц.

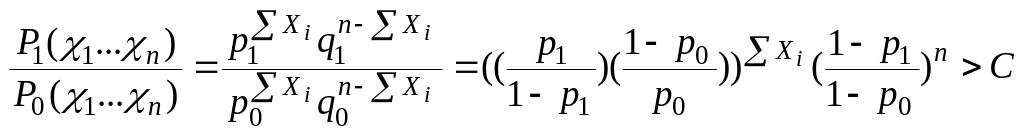
Пусть >

, - const для данной выборки

Если бы , то знак был бы на оборот.

т.к. число единиц в должно быть больше

Вариант 1: Считать суммы для разных .

Вариант 2:

,

графики

При увеличении n аргумент Ф будет стремиться к , то есть ошибка второго рода будет уменьшаться.

Вопрос.

Если N(a₀,1), N(a₁,1), то критическая область выглядела бы следующим образом

Если , то критическая область имела вид

Если то как будет выглядеть критическая область ????