Особенности

• Если произошла рассинхронизация, то через n тактов S заполнятся снова одинаково, т.е. происходит автоматическая синхронизация. Следовательно нет необходимости устанавливать начальное состояние. Перед текстом передается последовательность одинаковых символов для синхронизации.

• Единичная ошибка искажает до n знаков.

• Система уязвима к имитации сообщений, следовательно необходимо вводить временные ограничения по передаче.

• Период гаммы не важен. Стойкость – на основе отображения.

Требования к гамме, вырабатываемой генератором синхронной поточной системы (периоды, линейная сложность, статистические свойства)

Линейная сложность последовательности - минимальная длина ЛРС (линейного регистра сдвига), который способен сгенерировать данную последовательность.

Для последовательности длины N максимальная линейная сложность N-1

Требования:

• Периоды почти всех вырабатываемых последовательностей должны быть большими.

• Выходные последовательности генератора не должны содержать длинных повторяющихся отрезков, что было бы равносильно повторному использованию гаммы.

• Выходные последовательности генератора должны обладать теми же свойствами, что и случайные последовательности.

• Зависимость между знаками выходной последовательности должна быть настолько сложной, чтобы ее восстановление по достаточно длинному отрезку являлось вычислительно сложной задачей.

Статистические свойства последовательностей. Постулаты Голомба

n₁ – число единиц («1») на периоде последовательности.

n₀ – число нулей («0») на периоде последовательности.

S_1,r – число серий из единиц длины r. (r штук единиц подряд)

S_0,r – число серий из нулей длины r.

– число единиц («1») в последовательности

- число нулей («0») в последовательности

Функция автокорреляции

Постулаты Голомба

• 

• где ,

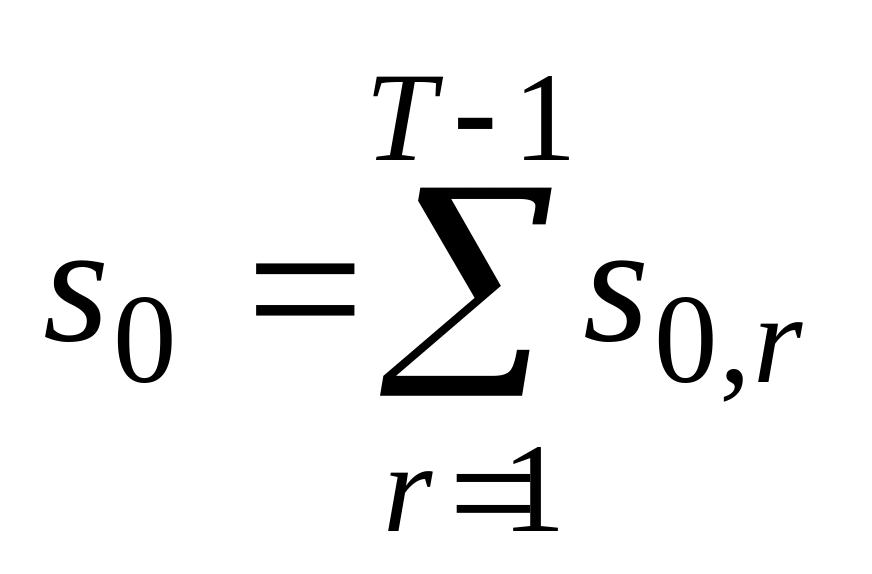
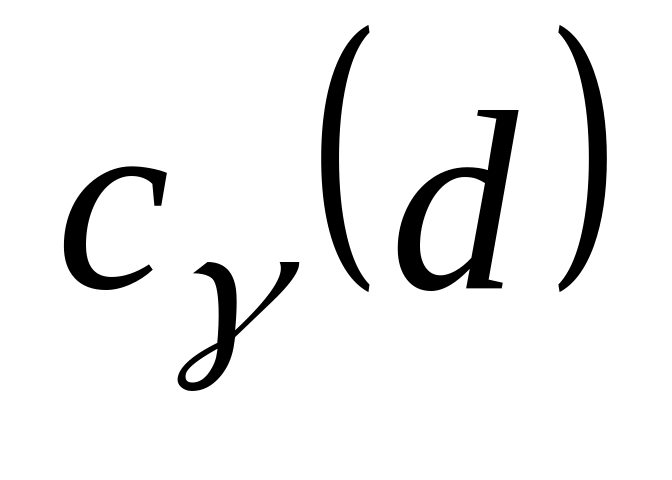• принимает не более двух значений

Если последовательность удовлетворяет этим постулатам, то она псевдошумовая..

Примером псевдошумовых последовательностей может служить ЛРС (линейный регистр сдвига) максимального периода. (Период ЛРС максимального периода равен )

Д-во:

1)

2) нестрого, но выполняется.

3) Доказать самостоятельно.(Так в лекциях)

Для проверки генераторов применяются статистические тесты

• Частотные

• Автокорреляционный

• Последовательный

• Тест серий

• Универсальный тест

• Тест повторений

• Их комбинации

При комбинировании тестов применяются статистики Фишера-Пирсона(если кол-во тестов небольшое) и Колмогорова-Смирнова.

Вывод о том, хороший ли генератор принимается тогда, когда доля последовательностей, принимаемых за случайные не отличается от того же для действительно случайного генератора.

Вопрос 25.2 Схемы шифрования и цифровой подписи Эль Гамаля и их модификации Схемы шифрования с открытым ключом и цифровой подписи. Основные принципы

Криптосистемы с открытым ключом используются непосредственно для передачи исключительно важных сообщений. Во многом подобные криптосистемам с секретным ключом криптосистемы с открытым ключом состоят из: пространства ключей K, а для каждого k из K, из пространств открытых сообщений M_K, пространств шифртекстов C_K и пар функций , таких что для любого открытого текста m из . Как и в криптосистемах с секретным ключом, эффективные алгоритмы для вычисления как E_K, так и D_K, должны легко получаться для каждого ключа k. Будем называть алгоритмы, полученные таким образом, естественными алгоритмами. Важной новой отличительной особенностью является то, что E_K должна быть однонаправленной функцией с секретом: необходимо, чтобы было практически невозможно построить никакого эффективного алгоритма для вычисления D_K (но только естественного алгоритма), зная описание естественного алгоритма для вычисления E_K.

В частности, это означает, что k не должно появляться в явном виде в естественном алгоритме шифрования.

Криптографические системы с открытым ключом используются следующим образом. Каждый пользователь раз и навсегда выбирает некоторый случайный ключ k из K. Он использует этот ключ для получения обоих естественных алгоритмов E_K и D_K. Затем он делает публично доступным свой алгоритм шифрования E_K, возможно посредством использования при этом некоторого справочника, но хранит в тайне свой алгоритм расшифрования D_K.

В том случае если другой пользователь захочет послать ему некоторое сообщение, то он найдет в справочнике его открытый алгоритм шифрования и использует его для того чтобы зашифровать свое сообщение. Тогда, используя собственный секретный ключ, только законный получатель сможет расшифровать это сообщение.

В противоположность криптосистемам с секретным ключом, заметим, что если пользователь А, закодировав некоторое сообщение m для пользователя В, сохранил шифртекст С, но потерял открытый текст (или забыл все, что в нем содержалось), то он не будет иметь никаких преимуществ перед нарушителем в раскрытии m из С.

Также в противоположность криптосхемам с секретным ключом, если нарушитель перехватывает шифртекст и знает для кого он был зашифрован, то он может использовать открытый алгоритм шифрования для проверки любого конкретного предположения о том, каким может быть соответствующий открытый текст. Возможность формировать шифртексты из открытых текстовых сообщений по своему выбору является причиной сокращения числа классических уровней атаки, которые обсуждались в связи с криптосистемами с секретным ключом.