1. Если а, (ав) – тавтологии, то тавтологией является в.

2. Если А – тавтология, содержащая пропозиционные переменные А₁, А₂, ..., А_n , и В получается из А подстановкой формул Ф₁, Ф₂, .. , Ф_n вместо А₁, А₂ , ... , А_n соответственно, то В есть тавтология, т.е. подстановка в тавтологию есть тавтология.

Пример 3. Показать, что формула F= A(BA) является тавтологией.

Предположим противное, т.е. A(BA) = 0. Тогда из определения импликации заключаем, что А = 1, а ВА = 0. Из равенства ВА = 0 следует, что В = 1, А = 0. Получили противоречие с тем, что А = 1.

Метод доказательства, который был использован в примере 3, называется методом от противного или методом косвенного доказательства.

Рассмотрим формулы Ф₁ =С&A и Ф₂ = (С)А. Заменим в формуле F примера 3 пропозиционную переменную А на Ф₁, а В на Ф₂, соответственно. Получим новую формулу F₁ = С&A((С)АС&A), которая по утверждению 2 является тавтологией. Убедимся в этом, составив для нее таблицу истинности.

Таблица 4.

А	С	(С)	(C)A	С&A	(C)AC&A	F1
0	0	1	1	0	0	1
0	1	0	0	0	1	1
1	0	1	1	0	0	1
1	1	0	1	1	1	1

Если в формуле F только А заменить на Ф₁, то получим еще одну тавтологию F₂ = С&A(BС&A).

Упражнение 1. С помощью таблицы истинности показать, что формула F₂ является тождественно–истинной.

С помощью определения 2 на множестве всех логических формул фактически задано бинарное отношение «равносильности» (=), которое, очевидно, является рефлексивным, симметричным и транзитивным. Таким образом, отношение равносильности логических формул является отношением эквивалентности, а значит, разбивает множество всех логических функций на классы эквивалентности. В частности тавтологии это класс эквивалентности, который содержит логическую константу 1, а тождественно ложные формулы – класс формул, эквивалентных, логической константе 0. Известно, что любой элемент из класса эквивалентности можно взять в качестве его представителя. На этом основаны, так называемые, эквивалентные преобразования логических формул, которые позволяют переходить от одних формул к другим, в определенном смысле более простым формулам, но эквивалентным (равносильным) данным. Это лежит в основе многих приложений математической логики и объясняет особый интерес к понятию равносильности. Очевидно, что, чем больше у нас в запасе равносильных соотношений, тем проще мы будем решать задачи упрощения логических формул.

Рассмотрим важнейшие равносильности алгебры логики.

1. Законы коммутативности:

А&В = В&А, АВ = ВА.

2. Законы ассоциативности:

(А&В)&С = А&(В&С); (АВ)С = А(ВС).

3. Законы дистрибутивности:

А&(ВС)= (А&В)(А&С), А(В&С) = (АВ)&(АС).

4. Законы идемпотентности:

А&A = A, AA = A.

5. Законы действий с константами:

А&1 = А, А&1 = 1, А0 = 0, А0 = А.

6. Закон противоречия:

А&А = 0.

7. Закон исключенного третьего:

АА = 1 -.

8. Закон двойного отрицания:

(А) = А.

9. Законы де Моргана:

(А&В) = (А)(В), (АВ) = (А)&(В).

10. Законы поглощения:

А&(BA) = A, A(B&A) =A.

Часть тождеств (1,6,7,8) очевидны, другие легко проверяются с помощью таблиц истинности.

Для примера докажем один из законов поглощения, не составляя таблицу истинности.

Пример 4. Доказать равносильность: А&(BA) = A.

Рассмотрим формулу F = А&(BA). Если в ней А = 1, то, очевидно, что BA = 1 при любом значении В, и тогда А& (BA) =1 как конъюнкция истинных высказываний. Пусть А = 0, тогда по определению конъюнкции А&(BA) = 0 при любых значениях В. Таким образом, во всех случаях значения формулы F совпадают со значениями А, что означает их равносильность, т.е. F=A.

Отметим, что логическая операция эквивалентности () и понятие равносильности связаны между собой следующим образом:

формулы F и H равносильны, т.е. F = H, тогда и только тогда, когда формула F  H – тавтология.

3.4. Полные системы связок

В этом разделе мы рассмотрим множество логических связок с точки зрения взаимозаменяемости его элементов. Кроме того, укажем множества логических связок, которых достаточно, чтобы получить все формулы алгебры высказываний. Такие системы связок называются полными.

Установим ряд равносильностей, которые выражают одни логические связки через другие.

1. А  В = (А)В.

2. А  В = (АВ)&(ВА).

3. А&В = ((А)(В)).

4. АВ = ((А)&(В)).

В пункте 3 мы уже доказали равносильность АВ = (А)В. Ясно, что равносильности 3 и 4 получаются из законов де Моргана, если взять отрицание формул, стоящих в левой и правой части, а затем воспользоваться законом двойного отрицания (см. п.3 формулы 9 и 8). Таким образом, в доказательстве нуждается равносильность 2.

Для доказательства равносильности 2 рассмотрим два случая.

1. Пусть А и В принимают одинаковые значения. Тогда АВ = 1, и АВ = 1, ВА = 1  (АВ)&(ВА) = 1. Следовательно, в этом случае обе части равносильности имеют одинаковые истинностные значения.

2. Пусть теперь А и В имеют различные логические значения. Тогда АВ = 0, и одна из импликаций АВ или ВА принимает значение 0, следовательно (АВ)(ВА) = 0. Таким образом, и в этом случае обе части равносильности имеют одинаковые логические значения.

Таким образом, равносильность 1 показывает, что в любой формуле связку «» можно исключить, заменив ее связками «» и «». Из равносильности 2 с учетом предыдущего равенства следует, что связка «» выражается через связки «&», «» и «». Значит система связок {&, , } является полной. А поскольку конъюнкция и дизъюнкция выражаются одна через другую с использованием отрицания (равносильности 3 и 4), то полными системами так же являются системы связок {&, } и {, }. Отметим, что системы {&, } и {, } минимальны, т.е. из них нельзя удалить ни одну из связок, не нарушая полноты.

Упражнение 2. Доказать равносильности:

АВ = (А)В,

A&B = ((A)B).

В результате будет показано, что система связок {, } так же является полной.

Однако существует логическая связка (операция), с помощью которых выражается любая из пяти, определенных ранее логических связок. Например, такой операцией является «штрих Шеффера». Она обозначается «|» и определяется следующей таблицей истинности:

Таблица 5.

A	B	A|B
0	0	1
0	1	1
1	0	1
1	1	0

Из таблицы 5 легко следует, что A&B = (А|B), а так как ,очевидно, что А = А|А, то A&В = (A|В)|(A|В). Таким образом, из полноты системы связок {&, } следует, что любую логическую формулу можно заменить на равносильную ей формулу, содержащую только штрих Шеффера.

3.5. Равносильные преобразования логических формул.

Под равносильными преобразованиями понимаются замена формулы или ее части (подформулы) на равносильную ей формулу, исходя из равносильностей 1–10 пункта 3 и равносильностей 1–4 пункта 4.

В силу свойства транзитивности отношения равносильности, если А₁=А₂, А₂=А₃, ..., А_k-1=А_k, то А₁=А_k. В таком случае будем для простоты записывать цепочку: А₁=А₂=А₃=...=А_k-1=А_k.

Приведем формулировки двух правил, с помощью которых можно переходить от одних формул к другим, равносильным данным, что позволит расширить запас равносильностей.

Теорема 1. (правило замены подформулы). Пусть С_А – логическая формула, содержащая А в качестве подформулы. Пусть С_В получается из С_А заменой А в этом вхождении на В. Тогда, если А = В, то С_А = С_В.

Доказательство теоремы 1 можно найти в [2].

Кроме того, полезно знать следующее правило подстановки формулы вместо переменной

Теорема 2. Пусть две равносильные формулы содержат переменную Х: F_X =H_X и формулы F_А и H_А получены заменой всех вхождений переменной Х на произвольную формулу А. Тогда F_А =H_А, т.е. равносильность сохраняется.

Равносильность F_X =H _X означает, что формула F_X  H_X является тавтологией, поэтому теорема 2 следует из утверждения 2 для тавтологий (см. п.3, стр. 40).

Заметим, что алгебраический аналог этих правил достаточно очевиден. Например, известное тождество а²–b²=(а–b)(а+b) можно использовать следующим образом: (са+cb)(a–b)=c(a–b)(a+b)=c(а²–b²) (подформулу заменили на эквивалентную ей формулу). С другой стороны из этого же тождества получаем: (sin²x)–b²=(sinx–b)(sinx–b) (все вхождения a заменили на функцию sinх).

Укажем важное отличие в использовании этих правил. В правиле подстановки формулы вместо переменной можно подставить произвольную формулу, но обязательно вместо всех вхождений переменной. Тогда как в правиле замены подформулы можно заменить только одно из вхождений подформулы, но не на любую формулу, а обязательно на равносильную формулу.

Покажем, как использовать правила равносильных преобразований, например, для упрощения формулы.

Пример 5. Упростить формулу ((АВ)АВ)&B.

Запишем цепочку равносильных формул:

((АВ)АВ)&B = (((АВ))АВ)&B = (АВАВ)&B =

= (АВ)&B = B.

Поясним наши преобразования. На первом шаге исключили импликацию, воспользовавшись равносильностью 1 (п.4). Затем, применили закон двойного отрицания. При этом в равносильности 8 все вхождения переменной А заменили на формулу (АВ). На следующем шаге использовали законы коммутативности дизъюнкции и идемпотентности. Наконец, воспользовались законом поглощения.

Этот же прием можно использовать и для доказательства тождественной истинности (ложности) формулы.

Пример 6. Доказать тождественную истинность формулы

F=(AB)((BC)(ABC)).

Запишем цепочку равносильных формул:

F=((AB))((BC))((AB))C)=

((A))&(B)((B))&(C)(A)&(B)C=

= A&(B)B&(C)(A)&(B)C =

= A&(B)(A)&(B)B&(C)C =

= (B)&(A(A))(BC)&((C)C) =

= (B)&1(BC)&1 =((B)B)C = 1C = 1.

3.6. Функции алгебры логики

Любая логическая формула задает некоторую функцию от входящих в нее элементарных высказываний. Действительно, каждое элементарное высказывание (аргумент) принимает одно из двух возможных значений – «истина» или «ложь» (1 или 0), при этом для любого набора значений аргументов сама формула также принимает одно из двух значений – «истина» или «ложь» (1 или 0).

Определение 4 Функцией алгебры логики от n переменных (или булевой функцией) называется произвольная n–местная функция f(x₁, x₂, ..., x_n), определенная на двухэлементном множестве В = {0,1} со значениями в этом же множестве В.

Ясно, что тождественно истинные формулы представляют собой постоянные функции, а две равносильные формулы выражают одну и ту же функцию алгебры логики.

До сих пор мы предусматривали логическую интерпретацию двоичных символов «0» и «1», однако она не является обязательной, поэтому будем рассматривать их как формальные символы, не имеющие арифметического смысла. Отметим, что булева функция по определению 4 является n–меcтной операцией. Обозначим через Р₂ множество всех логических функций, а через Р₂(n) – множество всех логических функций от n переменных. Тогда алгебра  =<B; Р₂>, образованная множеством В = {0,1} со всеми возможными операциями на нем, называется алгеброй логики.

Всякая логическая функция (другое, более распространенное название функция алгебры логики) n переменных может быть задана таблицей, в левой части которой перечислены все 2ⁿ наборов значений переменных, а в правой части – значения функции на этих наборах.

Пример 7. Задать таблицей функцию принятия решения «кабинетом трех» при условии, что каждый голосующий говорит либо «да», либо «нет», а решение принимается большинством голосов.

Таблица 6.

x1	x2	x3	f (x1, x2, x3 )
0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 0 0 1 0 1 1 1

Наборы значений аргументов, для которых функция f=1, часто называют единичными наборами этой функции. Соответственно наборы, на которых функция обращается в нуль – нулевыми наборами.

В таблице наборы значений аргументов функции, как правило, располагают в лексико–графическом порядке, который заключается в том, что, рассматривая наборы как двоичные числа, записывают их в порядке возрастания. При любом фиксированном упорядочении наборов логическая функция n переменных однозначно определяется вектор‑столбцом ее значений. Поскольку, такой вектор имеет размерность 2ⁿ, то число |Р₂(n)| различных функций n переменных равно числу различных двоичных векторов длины 2ⁿ, т.е.

|Р₂(n)|= . (2)

Переменная x_k функции f(x₁, ..., x_k-1, x_k, x_k+1, ..., x_n) называется фиктивной, если f(x₁, ...,x_k-1, 0, x_k+1, ..., x_n)=f(x₁, ..., x_k-1, 1, x_k+1, ..., x_n) при любых значения остальных переменных. В этом случае ясно, что, удалив фиктивную переменную, получим функцию, которая зависит от n–1 переменной. Смысл удаления фиктивных переменных очевиден. Однако иногда бывает полезно вводить фиктивные переменные, так как это позволяет любую конечную совокупность функций считать зависящей от одного и того же множества переменных. В частности, равенство (2) имеет место при условии, что Р₂(n) содержит все возможные функции n переменных, в том числе и функции с фиктивными переменными.

Рассмотрим логические функции одной и двух переменных. Логических функций одной переменной х четыре, они приведены в следующей таблице.

Таблица 8.

х	0	1	2	3
0 1	0 0	0 1	1 0	1 1

Функции ₀ и ₃ представляют собой константы 0 и 1, соответственно; их значения не зависят от значения переменной, т.е. х – фиктивная переменная. Функция ₁(х)=х, а функция ₂(х) совпадает с операцией отрицания, т.е. аналитически может быть представлена формулой ₂(х)=х.

Различных логических функций двух переменных 16; они приведены в следующей таблице.

Таблица 9.

x1	x2	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0 0 1 1	0 1 0 1	0 0 0 0	0 0 0 1	0 0 1 0	0 0 1 1	0 1 0 0	0 1 0 1	0 1 1 0	0 1 1 1	1 0 0 0	1 0 0 1	1 0 1 0	1 0 1 1	1 1 0 0	1 1 0 1	1 1 1 0	1 1 1 1

Функции ₀(x₁, x₂)=0 и ₁₅(x₁, x₂)=1 – константы, т.е. функции с двумя фиктивными переменными. Функции ₃(x₁, x₂)=х₁, ₅(x₁, x₂)=х₂ совпадают с одной из переменных, а ₁₀(x₁, x₂)=x₂ и ₁₂(x₁, x₂)=x₁ с отрицанием одной переменной, имея в качестве фиктивной другую переменную. Сравнивая значения функций в таблице 2 с таблицами истинности для логических операций, заключаем, что вполне естественно функцию ₁(x₁, x₂) назвать конъюнкцией и обозначить ₁(x₁, x₂)=x₁&x₂, функцию ₇(x₁, x₂)=x₁  x₂ – дизъюнкцией, ₉(x₁, x₂)=(x₁ x₂) – эквивалентностью, ₁₃(x₁, x₂)=(x₁ x₂) – импликацией. Иногда символ & опускают и записывают: ₁(x₁, x₂)=x₁ x₂.

Еще три функции имеют свои обозначения: ₆(x₁, x₂)=x₁x₂ – сложение по модулю два (неравнозначность), ₈(x₁, x₂)=x₁x₂ – стрелка Пирса, ₁₄(x₁, x₂)=x₁|x₂ – штрих Шеффера. Остальные функции специальных названий не имеют, однако легко выражаются через перечисленные ранее функции.

Упражнение 3. Проверить справедливость следующих равенств:

₂(x₁, x₂)=(x₁x₂), ₄(x₁, x₂)=x₂x₁, ₈(x₁, x₂)=(x₁x₂),

₁₁(x₁, x₂)=(x₂x₁), ₁₄(x₁, x₂)=(x₁&x₂).

Заметим, что ₄(x₁, x₂)=₁₃(x₂, х₁), т.е. функция ₄ получена из импликации переименованием переменных, а функция ₁₄ является результатом подстановки в функцию ₁₂(x₁, x₂) функции ₁(х₁, х₂), вместо аргумента x₁, т.е. ₁₄(x₁, x₂)=(x₁&x₂)=₁₂(₁(х₁, х₂), х₂). Таким образом, приходим к очень важному понятию.

Функция f называются суперпозицией функций f₁, f₂ , ... , f_m, если она получена с помощью подстановки этих функций друг в друга и переименования переменных. Выражение, описывающее эту суперпозицию, называется формулой. Сформулируем более точно понятие формулы.

Пусть ={f₁, f₂, ..., f_m, ...}-некоторое множество функций алгебры логики, т.е. подмножество множества Р₂. Каждая функция f(х₁, ..., х_n) есть формула над . Пусть f_о(х₁, х₂, ..., х_n) – функция n переменных из  и А₁, А₂, .. , А_n – либо формулы над , либо символы переменных, тогда f_о(А₁, А₂, .. , А_n) – формула над . Других формул над  нет.

Любая формула F_k , которая используется в построении формулы F, называется ее подформулой. При этом все подформулы F_k являются подформулами F.

3.7. Разложение логической функции по переменным. Совершенная дизъюнктивная нормальная форма (СДНФ)

Для любой логической функции, отличной от константы, существует представление ее в некотором стандартном виде, который является частным случаем более общего представления – разложения Шеннона.

Введем обозначения: х⁰=х, х¹=х. Пусть  – параметр, равный 0 или 1. Тогда легко проверяется, что х^=1  х=.

Теорема 3. Всякая логическая функция f(х₁, ..., х_n) представима в следующем виде:

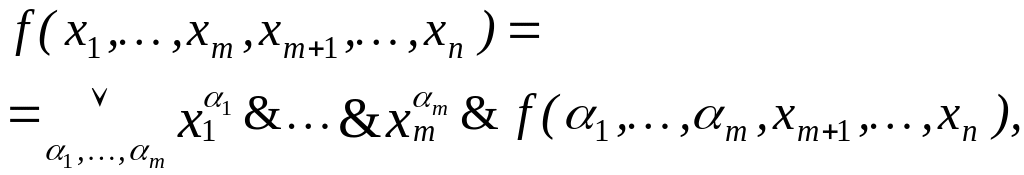(3)

где mn, а дизъюнкция берется по всем 2^m наборам переменных х₁, ..., х_m.

Доказательство. Для доказательства теоремы вычислим значение правой части равенства (3) для произвольного набора значений переменных: . Убедимся, что оно совпадает со значением . Только для одной из всех 2^m конъюнкций вида в правой части соотношения (3) выполняются равенства: ₁=₁, ..., _m=_m. Поскольку х^ =1  х=. то, только эта конъюнкция равна 1, а все остальные конъюнкции равны 0. В силу тождеств: а  0 = 0 и а1= а правая часть равенства (3) принимает вид:

.

Равенство (3) называется разложением Шеннона или разложением функции по переменным х₁, ..., х_m.

Для простоты записи принято опускать знак конъюнкции, т.е. писать ху вместо x&y, и отрицание обозначать с помощью черты над переменной, т.е. х= . С учетом этих соглашений в качестве примера запишем разложение Шеннона для функции четырех переменных (n=4) по переменным (m=2).

При m=1 из (3) получаем разложение по одной (любой) переменой, которое имеет вид:

Важнейшим частным случаем формулы (3) является разложение по всем переменным (m=n). При этом все переменные в правой части принимают фиксированные значения, и значения функции в конъюнкциях становятся равными 0 или 1, следовательно, остаются только те конъюнкции, в которых функция имеет значение 1. Таким образом, получаем:

(4) где дизъюнкция берется по всем наборам (₁, ..., _n), на которых функция принимает единичное значение. Такое разложение называется совершенной дизъюнктивной нормальной формой (СДНФ) функции f .

Исходя из формулы (4), можно сформулировать следующий алгоритм построения СДНФ по таблице истинности:

1. выделяем в таблице истинности единичные наборы;

2) каждому единичному набору сопоставляем дизъюнктивное слагаемое, т.е. конъюнкцию переменных, причем переменная берется без отрицания, если она в этом наборе имеет значение 1 и с отрицанием, если – 0.

Пример 8. Представить в совершенной дизъюнктивной нормальной форме (СДНФ) функцию f(х₁, х₂, х₃) заданную таблицей.

Таблица 10.

х1	х2	х3	f( х1, х2, х3 )
0	0	0		0
0	0	1		0
0	1	0		1
0	1	1		1
1	0	0		0
1	0	1		0
1	1	0		1
1	1	1		1

Для построения СДНФ выделяем в таблице единичные наборы, их четыре: (0,1,0), (0,1,1), (1,1,0), (1,1,1). Таким образом, СДНФ состоит из четырех дизъюнктивных слагаемых и согласно формуле (4) имеет вид:

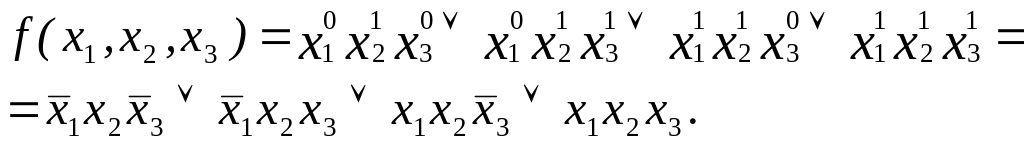
Из теоремы 3 и определения СДНФ легко следует

Теорема 4. Всякая логическая функция f(х₁, ..., х_n), которая не равна тождественно 0, единственным образом (с точностью до перестановки дизъюнктивных слагаемых) представима в виде СДНФ.

Таким образом, получаем, что каждая СДНФ является универсальным представителем целого класса равносильных формул, так как все равносильные формулы имеют одну и ту же СДНФ.

Дадим точное определение СДНФ.

Определение 5 Совершенной дизъюнктивной нормальной формой (СДНФ) функции f(х₁, ..., х_n) называется формула F, которая представляет собой дизъюнкцию конъюнкций переменных х₁, ..., х_n либо их отрицаний, причем выполняются следующие условия:

1. каждое дизъюнктивное слагаемое содержит все n переменных;

2. все дизъюнктивные слагаемое различны;

3. ни одно дизъюнктивное слагаемое не содержит одновременно переменную и отрицание этой переменной;

4) ни одно дизъюнктивное слагаемое не содержит одну и ту же переменную дважды.

3.8. Двойственность. Принцип двойственности.

Определение 6 Булева функция f(х₁, ..., х_n) называется двойственной к функции f*(х₁, ..., х_n), если

f(х₁, ..., х_n)=f*(х₁, ...,х_n) (5)

Если в равенстве (5) взять отрицание над обеими частями равенства и подставить вместо переменных х₁, ..., х_n их отрицания, то получим, что f*(х₁, ..., х_n) двойственна к f(х₁, ..., х_n), т.е. отношение двойственности симметрично. Ясно, что для любой функции двойственная функция определяется однозначно. Функция называется самодвойственной, если она двойственна себе, т. е. .

В силу закона де Моргана (х у) = (х у) и закона двойного отрицания имеем: ху = (ху). Последнее равенство показывает, что дизъюнкция и конъюнкция – двойственные друг другу функции. Очевидно, что двойственные функции константы 1 и 0, а отрицание – самодвойственная функция.

Упражнение 4. Показать, что f(x, y, z)=xy  xz  yz – самодвойственная функция.

Сформулируем принцип двойственности: если в формуле F, представляющей функцию f, все знаки функций заменить двойственными им, то полученная формула F*, будет представлять функцию f*, двойственную f.

Отсюда получаем важное утверждение.

Теорема 5. Если формулы F и G равносильны (F=G), то и двойственные им формулы F* и G* равносильны (F*=G*).

В булевой алгебре принцип двойственности реализуется следующим образом: если в булевой формуле F, представляющей функцию f, все конъюнкции заменить дизъюнкциями, дизъюнкции конъюнкциями, 0 заменить 1, а 1 заменить 0, то получим формулу F*, которая представляет функцию f*, двойственную f . Теорема 5 расширяет запас равносильностей в булевой алгебре. Например, закон исключенного третьего А(А) = 1 можно рассматривать, как равносильность, полученную из закона противоречия А&(А) = 0. Это замечание относится к каждой паре равносильностей 1, 2, 3, 4, 9, 10 из списка важнейших равносильностей булевой алгебры, приведенных в пункте 3.

Принцип двойственности можно использовать для представления логической функции в совершенной конъюнктивной нормальной форме (СКНФ).

Сформулируем определение СКНФ как определение, двойственное определению СДНФ (см. определение 5).

Определение 7 Формула F называется совершенной конъюнктивной нормальной формой (СКНФ), если она представляет собой конъюнкцию дизъюнкций переменных х₁, ... , х_n либо их отрицаний, причем выполняются следующие условия:

1. каждый конъюнктивный сомножитель содержит все n переменных;

2. все конъюнктивные сомножители различны;

3. ни один конъюнктивный сомножитель не содержит переменную и отрицание этой переменной;

4) ни один конъюнктивный сомножитель не содержит одну и ту же переменную дважды.

Ясно, что если формула F – СДНФ функции f(х₁, ..., х_n), то двойственная формула F* представляет собой СКНФ для двойственной функции

. Исходя из этого, можно сформулировать алгоритм построения СКНФ по таблице истинности.

В таблице истинности функции f(х₁, ..., х_n) выбираем все нулевые наборы и каждому такому набору сопоставляем дизъюнкцию переменных, в которой переменная х_k записывается с отрицанием, если х_k=1 и без отрицания в противном случае. Например, для функции из примера 8 СКНФ имеет вид:

.

В силу принципа двойственности справедлива теорема, двойственная теореме 4.

Теорема 5. Всякая логическая функция f(х₁, ..., х_n), которая не равна тождественно 1, единственным образом (с точностью до перестановки конъюнктивных сомножителей) представима в виде СКНФ.

Таким образом, совершенная нормальная форма (СКНФ) является представителем целого класса равносильных формул, которые задают одну и ту же логическую функцию.

3.9. Дизъюнктивные и конъюнктивные нормальные формы. Проблема минимизации

Тот факт, что СДНФ и СКНФ являются универсальными представителями класса равносильных формул, определяет их важную роль в алгебре логики. Но с другой стороны, именно в силу их универсальности, они не являются простейшими представителями этого класса. Во многих прикладных задачах приходится находить среди равносильных формул наиболее «простые» в определенном смысле формулы. Это и составляет суть проблемы минимизации.

Очевидно, что СКНФ функции из примера 8 можно упростить, например, так:

=

.

При этом конечная формула сохранила структуру исходной, т.е. является конъюнкцией дизъюнкций переменных и их отрицаний, но в ней не выполняются условие 1) определения 7.

Убирая ряд ограничений из определений СДНФ (СКНФ), приходим к понятию дизъюнктивной (конъюнктивной) нормальной формы – ДНФ (КНФ).

Определение 8 Элементарной конъюнкцией n переменных называется конъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более одного раза.

Определение 9 Дизъюнктивной нормальной формой (ДНФ) формулы F называется равносильная ей формула, которая представляет собой дизъюнкцию (возможно одночленную) элементарных конъюнкций.

Для любой формулы алгебры логики путем равносильных преобразований можно получить ее ДНФ, причем не единственную.

Пример 9. Представить формулу F = (xy)ху в дизъюнктивной нормальной форме.

Заменяя импликацию, имеем – это ДНФ формулы F, так представляет собой трехчленную дизъюнкцию элементарных конъюнкций. Проводя дальнейшие упрощения с помощью закона дистрибутивности, получаем: Последняя формула также является ДНФ, но с меньшим числом дизъюнкций и переменных.

Двойственным образом можно определить конъюнктивную нормальную форму.

Определение 10 Элементарной дизъюнкцией n переменных называется дизъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более одного раза. Конъюнктивной нормальной формой (КНФ) формулы F называется равносильная ей формула, которая представляет собой конъюнкцию (возможно одночленную) элементарных дизъюнкций.

Чтобы получить ДНФ (КНФ), если функция f(х₁, ..., х_n) задана таблицей, можно построить СДНФ (СКНФ), а затем упростить ее до ДНФ (КНФ), используя равносильности алгебры логики.

Если функция задана с помощью формулы F(х₁, ..., х_n), то приведение ее к ДНФ (КНФ) можно осуществить с помощью эквивалентных преобразований в булевой алгебре по следующей схеме.

1. Если формула F(х₁, ..., х_n) не является булевой, т.е. содержит символы «» и «», то используя равносильности 1, 2 п. 3.4, переходим к равносильной ей булевой формуле.

2. С помощью законов де Моргана (см. равносильности 9, п. 3.3) все отрицания «спускаем» до переменных, убирая при этом двойные отрицания (см. равносильность 8, п.3.3).

3. На основании законов дистрибутивности (см. равносильности 3, п. 3.3) раскрываем скобки.

4. С помощью законов идемпотентности, противоречия и исключенного третьего (см. равносильности 4, 6, 7, п. 3.3) удаляем лишние конъюнкции и повторы переменных в конъюнкциях.

5. Используя равносильности 4, пункта 3.3, удаляем константы 0 и 1.

Если на третьем шаге используем закон дистрибутивности конъюнкции относительно дизъюнкции, т.е. А&(ВС)= (А&В)(А&С), то в результате указанных преобразований получаем ДНФ формулы F. В случае применения двойственного закона дистрибутивности дизъюнкции относительно конъюнкции: А(В&С) = (АВ)&(АС) получаем КНФ формулы F.

Далее всякую ДНФ можно привести к СДНФ, расщеплением конъюнкций, которые содержат не все переменные, с помощью тождества, которое называется законом расщепления или склеивания:

A = (А&B)(A&B) (6)

Для перехода от КНФ к СКНФ поступают аналогично, но используют двойственный закон расщепления:

A = (AB)&(AB). (7)

Пример 10. Формулу F = ((xy)z)(xyz) привести к ДНФ и СДНФ.

Поскольку формула содержит импликацию, то алгоритм приведения к ДНФ начинается с пункта 1.

1. F = ((xy)z)(xyz) = |AB = AB| =((xy)z)(xyz). Получили равносильную булеву формулу.

2. F=((xy)z)(xyz) = |(AB)=AB| = (xy)z)(xyz). Получили формулу, в которой отрицания относятся только к переменным.

3. F = ((xy)z)(xyz) = |(AB)C=(AC)(BC)| =

= xxxyxzxyzyyzyzz.

4. F = xxxyxzxyzyyzyzz = |AA=0, AA=A| = 0xyxzxyz0zyz.

5. F =0xyxzxyz0zyz = |0A=A, 0A=0| =

= xyxzxyzyz.

Получили ДНФ формулы F.

Опуская знаки конъюнкции, и заменяя символ отрицания «» на черту над переменной, получаем:

Данная формула допускает следующее упрощение:

|A1=1,1&A=A| =

=

Чтобы получить СДНФ, можно взять любую из полученных ДНФ и «расщепить» все неполные конъюнкции. Возьмем последнюю ДНФ и воспользуемся равенством (6), тогда получим:

|AA=A| =

= .

Последняя формула представляет собой СДНФ исходной формулы .

Для приведения формулы F к КНФ нужно выполнить без каких–либо изменений первые два шага преобразований, а на третьем шаге воспользоваться двойственным законом дистрибутивности. В результате получим:

F = ((xy)z)(xyz) = |(AB)C=(AC)(BC)| =

= (xyz)(xy)(хz).

В данном случае сразу получили КНФ, которая, впрочем, допускает упрощение. Для получения СКНФ «расщепляем» второй сомножитель с помощью переменной z, а третий – с помощью переменной у, используя двойственный закон расщепления (7):

F =(xyz)(xy)(хz) =

(xyz)(xyz)(хyz)(xyz)(хyz) =

= (xyz)(xyz)(хyz)(хyz),

или иначе,

.

Пусть F и G две равносильные формулы, т.е. F=G. Как показано выше, существуют эквивалентные преобразования, которые приводят F и G к СДНФ. По теореме 4 СДНФ этих формул совпадают. Если сначала преобразовать F к СДНФ, а затем обратить преобразования, с помощью которых G приводится к СДНФ, то в результате эквивалентными преобразованиями из F получим G.

Таким образом, справедлива следующая теорема.

Теорема 6. Для любых двух равносильных формул F и G существует эквивалентное преобразование F в G c помощью основных равносильностей булевой алгебры логики (равносильности 1 –10, п.3.3).

Выше было показано, что любую булеву функцию можно представить формулой в виде ДНФ или КНФ. Эквивалентными преобразованиями в общем случае можно получить равносильную формулу, содержащую меньшее, чем исходная формула, число переменных. Если при этом рассматривать только ДНФ данной функции, то возникает задача минимизации в классе ДНФ.

ДНФ называется минимальной, если она содержит наименьшее общее число вхождений переменных по сравнению со всеми равносильными ей дизъюнктивными нормальными формами.

Отметим, что минимальная ДНФ определяется неоднозначно. Для конечного числа переменных, число равносильных ДНФ конечно, следовательно, минимальную ДНФ можно найти, перебрав все равносильные ДНФ и выбрав среди них ту, которая содержит минимальное число переменных. Однако при большом числе переменных такой перебор практически невыполним. Существуют эффективные способы нахождения минимальных ДНФ (см., например, Яблонский С. В. Введение в дискретную математику). Мы приведем без обоснования только один из методов – метод минимизирующих карт, который не отличается большой эффективностью, но прост в изложении и не требует введения новых понятий.

Пусть булева функция задана таблицей или известна ее СДНФ (при записи формул будем опускать знаки конъюнкции и знак отрицания «» заменять чертой над переменной).

Составим минимизационную карту. Она представляет собой таблицу, в которой каждая строка соответствует некоторой элементарной конъюнкции от n переменных – , где _k{0,1}, k = 1, 2, ..., n. Именно такая конъюнкция является элементом последнего столбца строки. А число строк в таблице равно числу всевозможных конъюнкций такого вида.

Начиная с первого столбца, в данной строке записывают сначала одноэлементные части этой конъюнкции: , затем двухэлементные: …, , …, …, , затем трехэлементные и так далее, причем переменные в любой конъюнкции записывают в порядке возрастания индексов переменных.

Если некоторая конъюнкция , из j-ой строки таблицы не входит в СДНФ минимизируемой функции f(х₁, ..., х_n), то это означает, что f(₁, ... , _n) = 0. Следовательно, любая конъюнкция из этой строки таблицы не входит ни в одну из ДНФ исходной функции.

Опишем алгоритм построения минимальной ДНФ.

1. Отметим в минимизационной карте все строки, которые соответствуют конъюнкциям не входящим в СДНФ данной функции f(х₁, ..., х_n). Вычеркнем все конъюнкции в этих строках.

2. Во всех остальных строках вычеркнем все те конъюнкции, которые были вычеркнуты в п.1.

3. В каждой строке, которая осталась после вычеркивания строк в пункте 1, выберем конъюнкции с наименьшим числом сомножителей, а остальные вычеркнем.

4. Составим все возможные ДНФ, выбирая в каждой строке только по одному оставшемуся элементу.

5. Среди всех ДНФ, построенных в пункте 4, выберем минимальную ДНФ.

Отметим, что последний пункт данного алгоритма предусматривает перебор различных ДНФ для нахождения минимальной, но число вариантов, в общем случае, меньше, чем тогда, когда перебираются все равносильные ДНФ.

Рассмотрим данный алгоритм на примере функции от 3-х переменных.

Пример 11. Минимизировать в классе ДНФ функцию

Составим минимизационную карту. Для функции трех переменных она будет иметь следующий вид.

Таблица 12.

* х1	* х2	*	*			* *
* х1	*	*	*		*	* *
*	* х2	* х3		*	*	* *
*	* х2	*		*		* *

В таблице 12 выделены строки, которые соответствуют конъюнкциям, не входящим в СДНФ. Значком * отмечены те конъюнкции, которые подлежат вычеркиванию по пункту 2, а значком ** – конъюнкции, которые вычеркиваются по пункту 3. После выполнения трех пунктов алгоритма таблица примет вид:

Таблица 13.

Перейдем к выполнению пункта 4. Составим из оставшихся конъюнкций все возможные ДНФ и упростим их.

(1) ;

(2) ;

(3) ;

(4) .

Очевидно, что минимальной ДНФ является первая, следовательно . Убедимся в справедливости данного равенства, для этого, используя правило расщепления, преобразуем полученную ДНФ к СДНФ:

.

3.10. Некоторые приложения алгебры логики

Еще в 1910 году физик П. С. Эренфест указал на возможность применения аппарата алгебры логики при исследовании релейно-контактных схем (РКС). Однако его идеи стали реализоваться значительно позднее, когда создание общей теории конструирования РКС стало остро необходимым.

В основе использования алгебры логики в конструировании и исследовании РКС лежит тот факт, что каждой схеме можно поставить в соответствие некоторую формулу алгебры логики, и каждая булева формула реализуется с помощью некоторой схемы.

Это позволяет, с одной стороны, выявить возможности данной схемы, изучая соответствующую ей формулу, а упрощение схемы свести к упрощению формулы. А с другой стороны, до построения схемы можно заранее описать с помощью формулы те функции, которые схема должна выполнять.

Рассмотрим подробнее, как устанавливается связь между формулами алгебры логики и переключательными схемами.

Под переключательной схемой понимают схематическое изображение некоторого устройства, состоящего из следующих элементов:

1) переключателей, которыми могут быть механически действующие устройства (выключатели, переключающие ключи, кнопочные устройства и т.д.), электромагнитные реле, электронные лампы, полупроводниковые элементы и т. п.;

2) соединяющих их проводников;

3) входов в систему и выходов из нее (клемм, на которые подается напряжение). Они называются полюсами системы.

Сопротивления, конденсаторы и т.д. на таких схемах не изображаются.

Переключательной схемой принимается в расчет только два состояния каждого переключателя, которые называют «замкнутым» и «разомкнутым».

Простейшей схеме, которая содержит один переключатель Х один вход А и один выход В (вход и выход на схеме буквами не обозначены), можно поставить в соответствие высказывание Х, причем Х – истинно, если переключатель замкнут (ток проходит) и Х – ложно в противном случае (ток не проходит) (схема 1).

Схема 1.

Булевым операциям (конъюнкции и дизъюнкции) также можно поставить в соответствие переключательные схемы.

Конъюнкция двух высказываний Х и Y представима двухполюсной схемой с последовательным соединением двух переключателей Х и Y, соответственно (схема 2).

Схема 2.

Очевидно, что данная схема пропускает ток тогда и только тогда, когда высказывания Х и Y одновременно истинны, т.е. истинна конъюнкция Х&Y.

Дизъюнкция двух высказываний Х и Y представима двухполюсной схемой с параллельным соединением двух переключателей Х и Y(схема 3).

Схема 3.

Эта схема пропускает ток в случае, когда истинно хотя бы одно из высказываний Х или Y, то есть когда истинна дизъюнкция ХY.

Более сложные двухполюсные переключательные схемы (П-схемы) могут быть построены из простейших схем 1, 2, 3 путем последовательного и параллельного их соединения.

Поскольку любая формула алгебры логики путем равносильных преобразований может быть записана в виде формулы, содержащей только операции конъюнкцию, дизъюнкцию и отрицание, то ясно, что всякая формула алгебры логики представима П-схемой и, обратно, любая П-схема может быть описана некоторой логической формулой.

Пример 12. Построить контактную схему для оценки результатов голосования при принятии решения «кабинетом трех» при следующих условиях: в случае, когда член кабинета голосует за принятие решения, он нажимает находящуюся в его распоряжении кнопку, в противном случае – не нажимает. Лампочка зажигается, если решение принято простым большинством голосов, то есть когда кнопки нажали не менее двух членов кабинета.

Ясно, что работа нужной РКС описывается булевой функцией от трех переменных f(x₁, x₂, x₃), где высказывание x_k означает: k-ый член кабинета голосует за принятие решения (k=1,2,3).

Функция f (x₁, x₂, x₃), очевидно, задается следующей таблицей:

Таблица 14.

0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Запишем СДНФ данной функции:

.

На схеме 4 изображена РКС, соответствующая этой формуле.

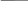
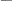
Схема 4.

Упростим СКНФ данной функции:

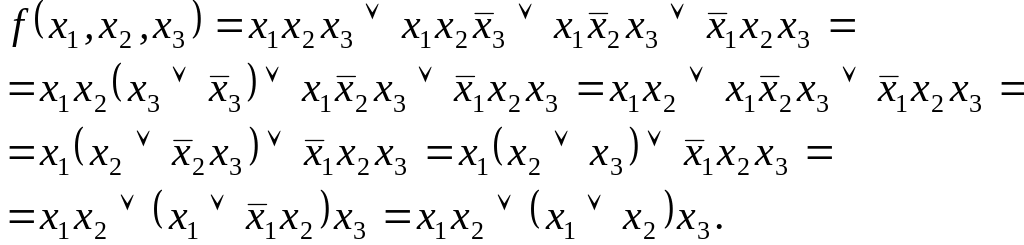
Таким образом, мы получили одно из возможных упрощений функции:

.

Согласно этой формуле функцию можно реализовать более простой РКС, которая состоит из пяти переключателей (схема 5).

Схема 5.

Рассмотрим теперь приложения алгебры логики к комбинационным схемам. Основные компоненты таких схем принято называть элементами. В наиболее общей форме элемент представляет собой устройство, которое имеет n входов и m выходов (m, nN). На каждый вход может подаваться один из двух бинарных сигналов (представим их как 0 и 1). С каждого выхода снимается одно из значений 0 или 1. Нам не потребуется много различных элементов, чтобы представить все возможные логические функции. На самом деле для схем, не имеющих временных задержек, можно ограничиться единственным типом элементов. Но более очевиден тот факт, что достаточно элементов трех типов, которые изображены на рис. 6.

&

a a

a



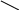
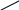c c c c

b b

“не” “и” “или”

а) б) в)

Рис. 6.

Первый элемент реализует операцию «отрицание» , второй – операцию «конъюнкция» (с=а&b) и третий – операцию «дизъюнкция» (с=аb).

Элементы «и» и «или» могут иметь более двух входов. В этом случае они определяются аналогично, т.е. выходной сигнал элемента «и» равен 1 тогда и только тогда, когда на всех входах сигнал равен 1, и выходной сигнал элемента «или» равен 1 тогда и только тогда, когда хотя бы один из входных сигналов равен 1.

Для представления более сложных функций элементы «соединяют» различными способами. Поясним сказанное примером.

Пример 13. Для схемы, изображенной на рис. 7 (точнее, части схемы), получить ее представление в виде функции алгебры логики, а затем упростить данную схему.





a

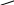
b

x



c y



Схема 7.

Анализируя схему, получаем представление для выходов x и y в виде логических функции:

и .

Поэтому

(при переходе к последнему выражению использован закон поглощения). Последней формуле соответствует схема 8, которая представляет собой одно из возможных упрощений схемы 7.



a

x



b

c y

Схема 8.

Применяя закон де Моргана к последней формуле ,

получаем эквивалентное выражение и соответствующую ему схему 9.

а

x





b

c

Схема 9.

Следовательно, мы можем использовать булевы выражения для анализа и упрощения сложных комбинационных схем. Рассмотренный выше пример дает представление, каким образом это делается.

В заключении отметим, что с помощью алгебры логики (булевой алгебры) можно решать логические задачи. Суть метода заключается в том, что, имея конкретные условия логической задачи, стараются записать их в виде формулы алгебры логики, затем путем равносильных преобразований упрощают полученную формулу. Простейший вид формулы, как правило, дает ответ на все вопросы задачи.