Когерентное рассеяние х-лучей

Всякое вещество, на которое падают Х-лучи, испускают вторичное излучение, длина которого равна первичной длине волны, либо близка к ней.

1. В случае рассеяния без изменения длины волны все атомы вещества образуют ансамбль когерентных источников, излучение которых может интерферировать

2. Благодаря тому, что в конденсированных средах межатомные расстояния по порядку величины равны длинам волн Х-лучей, возможна интерференция.

3. Энергия рассеяния не распределяется по всему пространству, а

4. концентрируется по отдельным направлениям, где рассеяние наиболее интенсивное – получаются дифракционные картины, по которым возможно определить взаимное расположение атомов.

На этих трех фактах основан рентгеноструктурный анализ. В основе рентгеноструктурного анализа лежит явление когерентного рассеяния Х-лучей конденсированными средами.

Рассеяние свободным электроном. Формула Томсона

П

усть свободный электрон находится в пучке параллельных Х-лучей интенсивностью (энергия, проходящая за 1 с через площадь 1 см²).

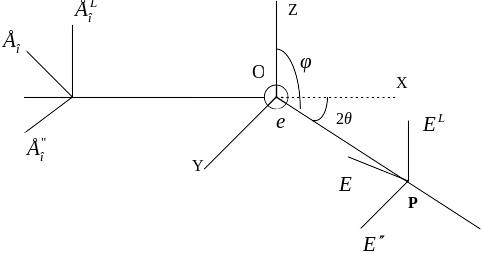
Пусть волна плоско поляризованная, электрический вектор ее распространяется по , встречает в точке О свободный электрон (рис.). Под действием переменного ускорения электрон начнет колебаться с амплитудой

. (1)

При этом он будет испускать электромагнитное излучение, которое в точке Р опишется вектором

, (2)

где - расстояние ОР, - угол между ОР и вектором ускорения электрона , электрический вектор лежит в плоскости ( , ). Т.е., в точку Р попадет излучение с амплитудой

. (3)

Выберем в качестве плоскости ХОУ плоскость, в которой лежат векторы , . Пусть угол рассеяния равен . Предположим, что в начальный момент времени вектор направлен по OZ нормально к плоскости

, . Тогда и

E_┴= (4)

Отношение интесивностей волны первичной (в точке О) и рассеянной (в точке Р) равно отношению квадратов амплитуд электрических полей

I_┴ = , т.к. (5)

I_┴ - поток энергии, пересекающий за 1 с площадь 1 см², расположенную в точке Р перпендикулярно . Эта площадь видна из точки О под телесным углом равным . Энергия рассеянного излучения, отнесенная к единице угла, будет

I_┴ = . (6)

Если предположить теперь, что первичный электрический вектор расположен в плоскости ХОУ, то, согласно (3) и (6) интенсивность в точке Р будет

. (7)

Поляризованный пучок всегда может быть разложен на два пучка, электрические векторы которых перпендикулярны и параллельны плоскости ХОУ в пропорции k_┴ и , k_┴+ =1. Тогда интенсивность рассеяния можно представить в виде

k_┴ I_┴+ = (k_┴+ ) . (8)

Если первичный пучок не поляризован, то k_┴ = =1/2, тогда (8) примет вид

(9)

Это формула Томсона.

При подстановке , , получим

. (10)

- энергия рассеяния внутри единицы телесного угла.

Интенсивность рассеяния пучка на расстоянии от точки рассеяния равна .

Формулы (8) и (9) являются фундаментальными в рентгеноструктурном анализе, т.к. все теоретические расчеты сводятся к определению рассеивающей способности данного объекта.

Применительно к ядру: интенсивность рассеяния одним протоном будет в раз слабее интенсивности рассеяния одним электроном. Этой величиной можно пренебречь.