Занятие 7 Тема: “Закон Био-Савара-Лапласа”

Преподаватель: Малацион Светлана Фиаловна

Цель занятия:

Усвоить фундаментальные понятия и законы электромагнетизма

Задача занятия:

Закрепить теоретический материал на тему “ Закон Био-Савара-Лапласа” на примере решения конкретных задач.

Компетенции, формируемые на занятии:

– способностью к кооперации с коллегами, работе в коллективе (ОК-3);

– способностью выявлять естественно-научную сущность проблем, возникающих в ходе профессиональной деятельности, привлекать для их решения соответствующий физико-математический аппарат (ПК-2);

Студент должен демонстрировать следующие результаты:

1) знать: основные физические законы электромагнетизма;

2) уметь: использовать для решения прикладных задач основные законы и понятия электромагнетизма;

3) владеть: навыками описания основных физических явлений и решения типовых задач.

Ключевые слова: Магнитное поле, линии магнитной индукции, магнитная постоянная, магнитная проницаемость среды, вектор магнитной индукции, вектор напряженности магнитного поля, правило правого винта, поле микро и макро токов, принцип суперпозиции магнитных полей, закон Био-Савара-Лапласа.

Основные понятия и законы

Магнитное поле – это силовое поле в пространстве, окружающем токи и постоянные магниты.

Характерная особенность магнитного поля – магнитное поле создается только движущимися зарядами и действует только на движущиеся в этом поле заряды.

Характер воздействия магнитного поля на проводник с током зависит от: 1) формы проводника 2) расположения проводника 3) направления тока.

Для исследования магнитного поля пользуются контуром (рамкой с током), размеры которого малы по сравнению с расстоянием до токов, образующих магнитное поле. Ориентация контура в пространстве определяется направлением нормали к контуру. Направление нормали определяется правилом правого винта: за положительное направление нормали принимается направление поступательного движения винта, головка которого вращается в направлении тока, текущего в рамке.

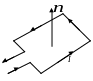
Рис. 1

Выбор направления магнитного поля. За направление магнитного поля в данной точке принимается направление, вдоль которого располагается положительная нормаль к свободно подвешенной рамке с током (рис.1), или направление, совпадающее с направлением силы, действующей на северный полюс магнитной стрелки, помещенной в данную точку (рис.2).

Рис. 2

Основные характеристики магнитного поля. На рамку с током в магнитном поле действует пара сил, которые создают вращающий момент М, зависящий как от свойств поля, так и от свойств рамки:  . Здесь – вектор магнитного момента рамки с током, – вектор магнитной индукции. Модуль вектора вращающего момента определяется формулой: ,

где  – угол между нормалью к плоскости рамки и вектором В.

При , и .

Магнитный момент рамки с током – зависит от силы тока в контуре и площади контура: .

Здесь S – площадь поверхности рамки с током; – единичный вектор нормали к поверхности рамки. Вектор совпадает с направлением нормали. Модуль вектора магнитного момента: . Тогда - максимальный вращающий момент рамки с током.

Магнитная индукция. Магнитная индукция в данной точке однородного магнитного поля определяется максимальным вращающим моментом, действующим на рамку с магнитным моментом, равным единице, когда нормаль к рамке перпендикулярна направлению поля

Магнитная индукция – силовая характеристика магнитного поля!

Линии магнитной индукции – линии, касательные к которым в каждой точке, совпадают с направлением вектора . Линии магнитной индукции всегда замкнуты и охватывают проводники с током

Направление линий магнитной индукции определяется по правилу буравчика. Если ввинчивать буравчик по направлению вектора плотности тока в проводнике, то направление движения рукоятки буравчика укажет направление магнитных силовых линий (рис. 3).

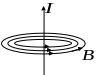
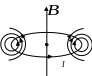
Рис. 3

Вблизи проводника линии магнитной индукции лежат в плоскостях, перпендикулярных проводнику.

Магнитное поле соленоида, как видно из рис. 4, подобно полю полосового магнита.

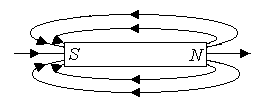
Рис. 4

Поле макро- и микротоков. Вектор магнитной индукции характеризует результирующее магнитное поле, создаваемое макро- и микротоками. Магнитное поле макротоков описывается вектором напряженности . Для изотропной однородной среды вектор магнитной индукции и вектор напряженности связаны следующим соотношением: . Здесь – напряженность магнитного поля, созданного макротоками; – магнитная постоянная (  Гн/м); – магнитная проницаемость среды, показывающая, во сколько раз магнитное поле, созданное макротоками ( ) усиливается микротоками среды (в вакууме ).

Закон Био-Савара-Лапласа и его применение к расчету полей. Закон Био-Савара-Лапласа позволяет найти вектор индукции магнитного поля, создаваемого малым линейным проводником с постоянным током (элементом тока): ,

где  вектор, численно равный длине dl элемента проводника и совпадающий по направлению с током;  радиус-вектор, проведенный из элемента dl в рассматриваемую точку поля; (рис. 5); k – коэффициент пропорциональности, который в системе СИ равен ,

где   безразмерная величина, характеризующая магнитные свойства среды и называемая относительной магнитной проницаемостью, для вакуума.

Рис. 5

Если учесть, что , то численное значение равно dB = .

Принцип суперпозиции. Магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций полей, создаваемых каждым током или движущимся зарядом в отдельности .

Магнитное поле прямого тока. Запишем закон Био-Савара-Лапласа в скалярном виде:

B= .

Ток течет по тонкому прямому проводу бесконечной длины. В качестве постоянной интегрирования выберем угол (рис. 6). Из треугольника АОВ видно, что AO = . Из треугольника АОС видно, что АО = ; Отсюда

dl = AO/ ; .

Рис. 6

Подставим полученные выражения для r и dl в формулу закона Био-Савара-Лапласа и запишем выражение для магнитной индукции поля прямого тока, текущего по проводу бесконечной длины.

dB = .

Проинтегрируем это выражение. Учтем, что угол 0 <  < π и получим следующую формулу для магнитной индукции поля прямого тока, текущего по проводу бесконечной длины:

; .

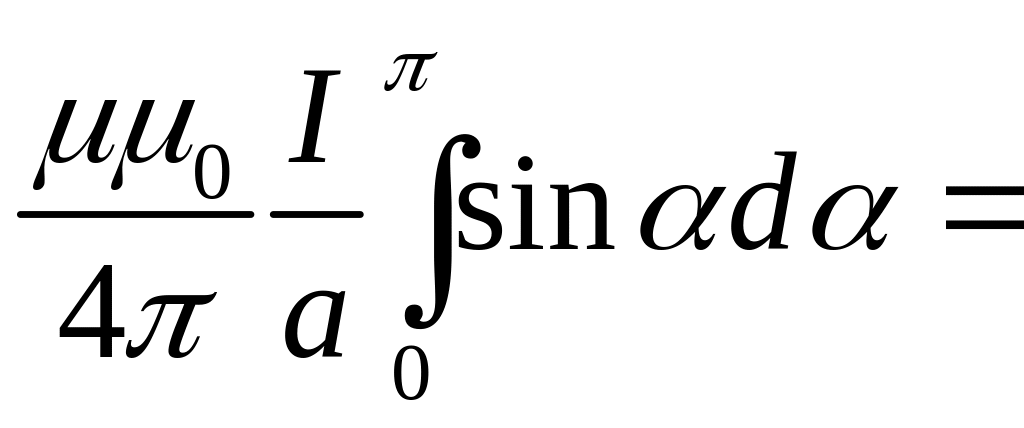
Магнитная индукция поля прямого тока, текущего по проводу конечной длины (рис. 7):

.

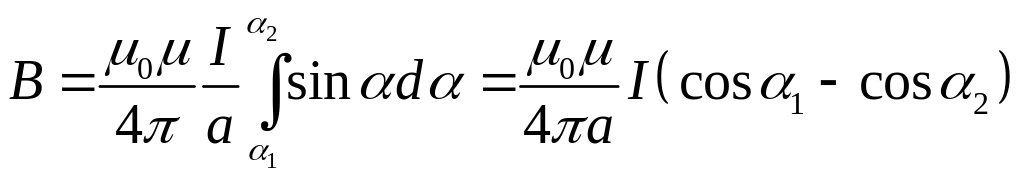Здесь а – кратчайшее расстояние от провода с током до точки, в которой определяется магнитная индукция поля.

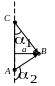
Рис. 7

Магнитное поле в центре кругового тока изображено на рис. 8.

Рис. 8

Все элементы кругового проводника с током создают в центре магнитные поля одинакового направления – вдоль нормали от витка. Сложение векторов можно заменить сложением их модулей. Учтем, что , sin  = 1, r = R и получим выражение для магнитной индукции в центре кругового тока.

; ;

.