Лабораторная работа № 4 приближенные методы решения дифференциальных уравнений в частных производных Общие сведения о дифференциальных уравнениях в частных производных
Постановка задач для уравнений в частных производных включает определение самого уравнения (или системы нескольких уравнений), а также необходимого количества краевых условий (число и характер задания которых определяются спецификой уравнения). Уравнения должны содержать частные производные неизвестной функции (или нескольких функций, если уравнений несколько) по различным аргументам, например, пространственной переменной х и времени t. Соответственно, для решения задачи требуется вычислить функцию нескольких переменных, например, u(x,t) в некоторой области определения аргументов 0<x<L и 0<t<T.
Линейным уравнением
в частных производных второго порядка
называется соотношение между функцией
(или
)
и ее частными производными вида:
(1.1)
В
случае, если F=0,
то уравнение (1.1)
называется
однородным, иначе – неоднородным.
Если В2-АС<0, то уравнение (1.1) относится к классу эллиптических уравнений; если В2-АС>0, то (1.1) – гиперболическое уравнение; если В2-АС=0, то (1.1) – параболическое уравнение.
В случае, когда В2-АС не имеет постоянного знака, получаем уравнение смешанного типа.
С помощью преобразования переменных x, y (или x, t) уравнение можно привести к виду, когда В=0. В этом случае очень просто определяется тип уравнения. Если А и С имеют один и тот же знак, то (1.1) относится к классу эллиптических уравнений; если разные, то – гиперболическое, а если А или С равно 0, то уравнение относится к параболическим.
Для нахождения единственного решения дифференциального уравнения в частных производных необходимо задать начальные и граничные условия. Начальными условиями принято называть условия, заданные в начальный момент времени t. Граничные условия задаются при различных значениях пространственных переменных. Для эллиптических уравнений задаются только граничные условия, которые можно разделить на три класса:
условие Дирихле:
.
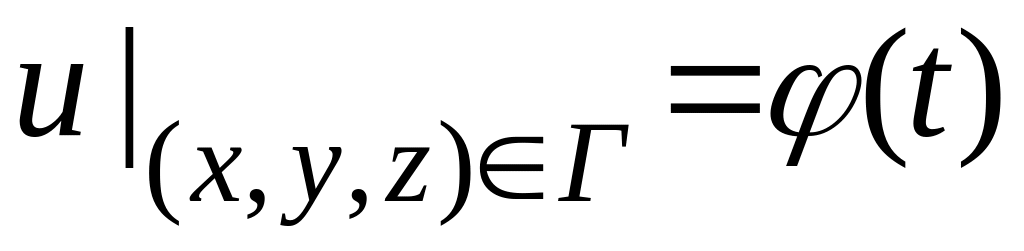В этом случае на
границе области Г, в которой ищется
решение, задана некоторая непрерывная
функция
.
В одномерном случае это условие принимает
вид:
где (0,L) – интервал, на котором ищется решение одномерной задачи;
условие Неймана:
.
В этом случае на границе области задана производная по направлению n внешней нормали;
- смешанное условие:
.
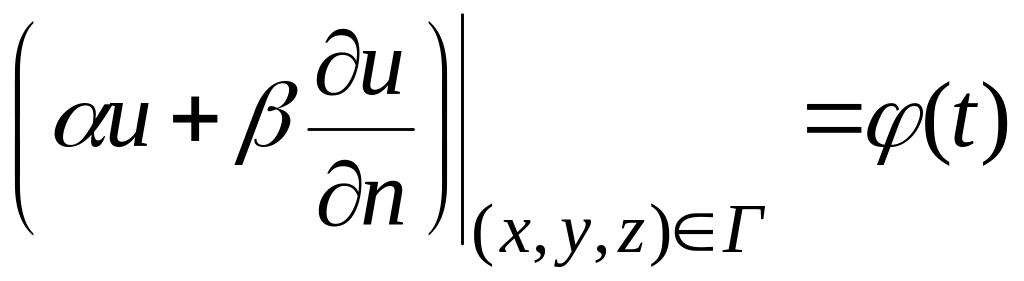Для параболических уравнений, кроме граничных условий, необходимо определить одно начальное, которое может быть таким:
.
В случае гиперболических уравнений начальные условия могут быть следующими:
и
Пакет partial differential equation (pde)
Пакет Partial Differential Equation (PDE) содержит средства для численного моделирования нестационарных физических полей, описываемых уравнениями в частных производных второго порядка. В пакете используется проекционный метод Галёркина с конечными элементами. Команды и графический интерфейс пакета могут быть использованы для математического моделирования физических полей в двумерной расчётной области применительно к широкому классу инженерных и научных приложений, включая задачи сопротивления материалов, расчёты электромагнитных устройств, задачи тепломассопереноса и диффузии.