17. Изменение матрицы квадратичной формы при замене базиса.

Матрица квадратичной формы А при переходе к другому базису будет меняться по следующей формуле: А’=Р^TАР

X=PX’, где Р – невырожденная матрица, Х – старые координаты, а Х’ - новые

Φ=(PX’)^TA(PX’)=X’^T(P^TAP)X’

Отсюда и видно, что матрица квадратичной формы в новых переменных будет А’=Р^TАР

18. Вывод канонического уравнения эллипса.

Для вывода уравнения эллипса выберем систему координат О_ху так, чтобы фокусы F₁ и F₂ лежали на оси О_х, а начало координат совпадало с серединой отрезка. Тогда фокусы будут иметь следующие координаты: F₁(-c;0) и F₂(c;0). Пусть М(х;у) — произвольная точка эллипса. Тогда, согласно определению эллипса, MF₁+MF₂=2a, т. е.

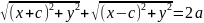
Это, по сути, и есть уравнение эллипса. Преобразуем уравнение к более простому виду следующим образом:

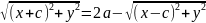
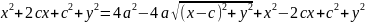
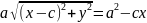
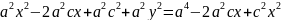
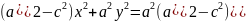
Так как по определению a>с, то a²-c²>0. Положим a²-c²=b². Тогда последнее уравнение примет вид b²x²+a²y²=a²b² или

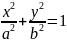
19. Вывод канонического уравнения гиперболы.

Для вывода уравнения гиперболы выберем систему координат О_ху так, чтобы фокусы F₁ и F₂ лежали на оси О_х, а начало координат совпадало с серединой отрезка. Тогда фокусы будут иметь следующие координаты: F₁(-c;0) и F₂(c;0). Пусть М(х;у) — произвольная точка гиперболы. Тогда, согласно определению гиперболы, |MF₁-MF₂|=2a

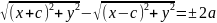
Это, по сути, и есть уравнение гиперболы. Преобразуем уравнение к более простому виду следующим образом:

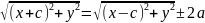
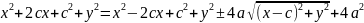
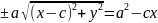
Так как по определению a<с, то a²-c²<0. Положим a²-c²=b². Тогда последнее уравнение примет вид b²x²-a²y²=a²b² или

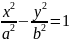
20. Выпуклость пересечения выпуклых множеств.

Пусть дано Х₁,...,Х_n - выпуклые множества. Обозначим 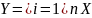- пересечение выпуклых множеств. Покажем, что Y - выпуклое множество. Для этого покажем, что для любых точек A,BY и для любого значения α in[0;1] точка M=αA+(1-α)B также принадлежит множеству Y: MY. Так как Y - суть пересечение выпуклых множеств Х₁,...,Х_n, то выбранные произвольным образом точки A, B принадлежат каждому из этих множеств X_i, i=1..n. В силу выпуклости каждого из множеств X_i по определению следует, что для произвольно выбранного значения α[0;1] точка M=αA+(1-α)B принадлежит каждому из множеств (все они выпуклы и содержат A,B). Так как все множества X_i содержат точку M, то и пересечение этих множеств также содержит точку M: MY. Из последнего включения в силу произвольности A,BY и произвольности параметра a[0; 1] следует выпуклость множества Y, что и требовалось показать.