11. Линейная независимость векторов, составляющих ортонормированную систему.

Система векторов v₁,…v_n называется ортонормированной если 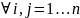выполняется: 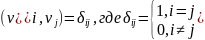- символ Кронекера.

Пример ортонормированной системы в R³:

х=(1,0,0), у=(0,1,0), z=(0,0,1) (х,у)=(у,z)=(х,z)=0, (х,х)=(у,у)=(z,z)=1

Док-во линейной независимости 3х3

Пусть x,y,z R³ – система ортонормированных векторов: х=(1,0,0), у=(0,1,0), z=(0,0,1) (х,у)=(у,z)=(х,z)=0, (х,х)=(у,у)=(z,z)=1

Предположим, что система векторов линейно зависима, то есть z=x+y. Тогда 0=(z,х)=(х+y,x)=(х,х)+(x,у)=

Мы получили, что =0, то есть z=у. Аналогично

0=(z,у)=(y,y)=(у,у)=

Мы получили, что ==0, а значит, z=0, что противоречит с тем условием, что (z,z)=1. Противоречие означает, что система ортонормированных векторов x,y,z R³ - линейно независима, что означает, что система трех линейно независимых векторов x,y,z является базисом в пространстве размерности 3.

12. Формулы для вычисления координат вектора в ортогональном базисе.

Рассмотрим евклидово пространство V с ортогональным базисом е₁,...,e_n. Тогда, для любого вектора āV выполнено 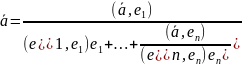. Другими словами, координаты вектора 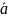в базисе е₁,...,e_n равны .

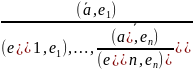Доказательство. Пусть 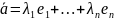– разложение вектора ā по базису, где

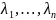- координаты вектора ā. Умножим скалярно обе части разложения вектора на e_i получим: 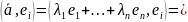и, следовательно, 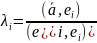. Отсюда и из разложения вектора следует формула вычисления координат в базисе.

13. Невырожденность ортогональной матрицы.

Матрица называется ортогональной, если А*А^Т=Е, то есть А^Т=А^-1

Пусть АR^nxn – ортогональная матрица. Предположим, что detA=0 (то есть, что ортогональная матрица – вырождена). По свойству определителей det(A*А^Т)=0. Но из определения ортогональности det(A*А^Т)=detE=1. Данное противоречие показывает, что любая ортогональная матрица невырождена.

14. Изменение матрицы линейного преобразования при замене базиса.

Изменение матрицы производится по формуле А’=T^-1AT

Пусть А – матрица линейного преобразования f в базисе 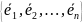. Предположим, что мы переходим к новому базису, в котором преобразованию отвечает новая матрица А’, а Т есть матрица перехода от исходного базиса к новому базису. Х=ТХ’, где Х – столбец из старых координат разложенного по базису вектора, а Х’ – столбец из новых координат. Аналогично Y=TY’. Учитывая, что Y=AX, Х=ТХ’ и Y=TY’, установим связь между Х’ и Y’.

Y’=T^-1Y=T^-1AX=T^-1ATX’. Отсюда следует, что матрицей отображения А в новом базисе будет матрица A’=T^-1ATX, что и требовалось доказать.

15. Равенство характеристических многочленов подобных матриц.

Рассмотрим подобные матрицы A и B = C^-1AC, где C - невырожденная матрица. Тогда

f_B=|B - λE|=|C^-1 AC - λE|=|C^-1AC – C^-1(λE)C|=|C^-1(A - λE)C|=|A - λE| = f_A Что и требовалось показать.

16. Ортогональность собственных векторов, соответствующих различным собственным значениям самосопряженного линейного преобразования.

Пусть φ: V→V – оператор, 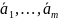– собственные векторы оператора φ, соответствующие собственным значениям λ₁,…,λ_m соответственно. Среди собственных значений λ₁,…,λ_m нет совпадающих. Тогда векторы линейно независимы

Доказательство. Доказываем индукцией по m. При m=1 лемма очевидна. Пусть m>1 и 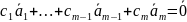- соотношение линейной зависимости. Мы должны доказать, что все коэффициенты равны нулю. Применив оператор φ к правой и левой частям равенства, получим

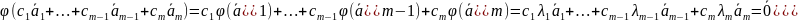
Умножая первое равенство на λ_m и вычитая из второго, получаем

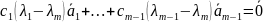
По индукции отсюда получаем, что 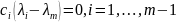. Из этого следует, что 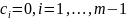, так как среди чисел λ₁,…,λ_m нет совпадающих.

Отсюда и из первого равенства следует, что 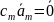и, следовательно, 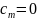. Таким образом, мы получили, что все коэффициенты соотношения линейной зависимости равны нулю. А значит ортогональность собственных векторов доказана.