1. Случайные погрешности

а) Инструментальные погрешности. Этот вид погрешностей проявляется во многих случаях, например, такие погрешнос­ти могут появиться при считывании показания по шкале, ес­ли шкала и стрелка не находятся в одной плоскости; в свою очередь, полученные данные зависят от угла, под которым человек смотрит на шкалу (так называемые погрешности па­раллакса). Также такие погрешности появляются из-за нео­пределенности, которая существует при оценке показаний прибора, когда стрелка находится между маркерами шкалы.

б) Погрешности из-за влияния окружающей среды. Эти по­грешности могут возрастать в результате изменения окружающиx условий, таких как изменение температуры или появ­ление электромагнитного воздействия.

в) Стохастические погрешности. Они появляются в результа­те стохастических процессов, таких как шум (см. главу 6).Стохастические процессы являются одной из причин слу­чайных возмущений.

2. Систематические погрешности

а) Конструкционные погрешности. Этот вид погрешностей обусловлен технологией производства на заводе-изготовите­ле и связан с допустимыми разбросами в размерах деталей и значениях электрических компонентов, используемых в дан­ном приборе.

б) Погрешности аппроксимации. Этот вид погрешностей воз­никает из-за сделанных предположений относительно зави­симостей между величинами. Например, линейная зависи­мость между двумя величинами часто только предполагает­ся, а на практике это предположение может оказаться только аппроксимацией к истинной зависимости.

в) Погрешности старения. Эти погрешности вызываются про­цессами старения приборов, так как детали изнашиваются и их характеристики изменяются, например из-за слоев грязи, окислов и т.д., скопившихся на поверхности деталей, изменя­ются сопротивление контактов и их изоляционные свойства

г) Погрешности подключения. Эти погрешности возникают, если включение приборов в измерительную цепь приводит к изменению значения самой измеряемой величины. Напри­мер, включение амперметра в электрическую цепь для изме­рения тока в ней приводит к изменению тока в этой цепи из-за сопротивления самого амперметра.

Разброс результатов

Результаты последовательности измерений одной и той же ве­личины могут быть построены в виде графика их частотного рас­пределения. Параметр «частота» показывает количество появле­ний некоторого значения или значений измеряемой величины внутри диапазона всех значений. Построенная зависимость час­тоты появления значений от самой измеряемой величины и есть частотное распределение (Рис. 3.1). Это распределение показыва­ет, как меняются значения, полученные в процессе измерений. Чем шире это распределение, тем меньше точность измерений.

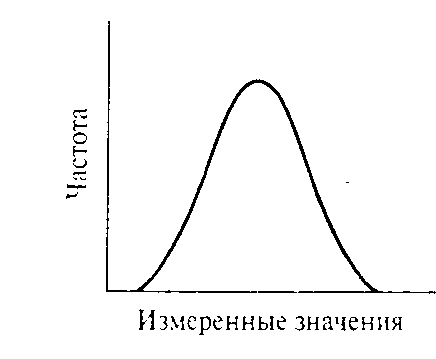
Рис. 3.1. Частотное распределение

При обработке серии проведенных измерений для представ­ления полученного результата часто используются следующие понятия:

1. Cреднее арифметическое значение ( ). Это сумма всех ре­зультатов измерений, деленная на количество рассматривае­мых измерений n

.

2. Мода. Это наиболее часто получаемое значение измеряемой ве­личины. Если частотное распределение симметрично, то мода и среднее значение будут равны. В случае несимметричности распределения, как на Рис. 3.2, эти величины будут различны.

Медиана. Это значение, которое делит частотное распреде­ление на две равные площади. В случае симметричности распределения медиана будет равна среднему значению.

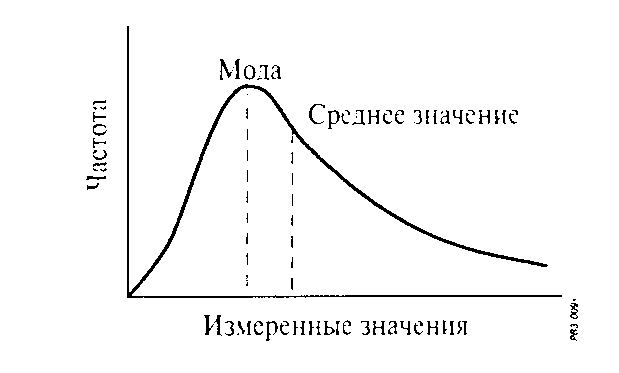
Рис. 3.2. Среднее значение и мода

Оценка точности или разброса частотного распределения проводится при помощи среднеквадратического отклонения (стандартного отклонения). Для измерения отклонение d — это разность между средним и полученным значениями. Сумма квадратов полученных отклонений ( ), деленная на количест­во измерений n, дает среднее значение квадратов отклонений. Квадратный корень из этого значения и есть среднеквадратическое отклонение, или стандартное отклонение 

.

Вероятная погрешность

Частотное распределение серии измерений показывает от­клонения, т.е. погрешности, результатов измерений от среднего значения. Частотное распределение обычно отображается в ви­де, показанном на Рис. 3.3. Эта форма представления называет­ся нормальным распределением Гаусса. Такое распределение показывает, что наиболее часто встречающееся значение изме­ряемой величины, у которого нет погрешности измерения, и есть среднее значение; что малая погрешность имеет большую вероятность, чем большая; и что вероятность получить резуль­тат измерения больше среднего значения на заданную величину погрешности равна вероятности получения результата меньше среднего значения на такую же величину погрешности.

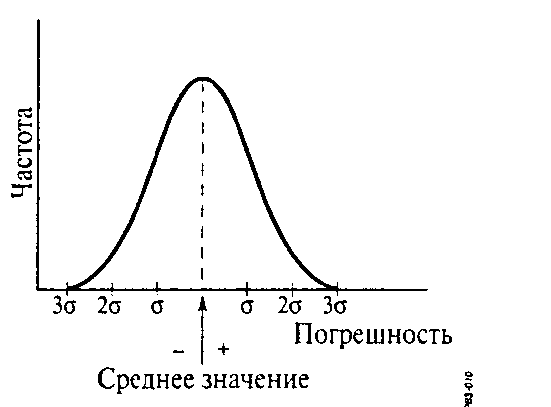
Рис. 3.3. Распределение Гаусса

По распределению Гаусса видно, что вероятность попадания результата измерения в интервал одного стандартного отклоне­ния от среднего значения равна 68.3%, в интервал двух стан­дартных отклонений — 95.5%, в интервал трех стандартных от­клонений — 99.7%, а четырех — 99.99%. Вероятность попада­ния результата измерения в интервал, составляющий +0.6745 от среднего значения, равна 50%. Интервал 0.6745 называется вероятной погрешностью.

Таким образом, фраза «вероятная погрешность для серии из­мерений» означает, что существует 50% вероятности того, что при произвольной выборке одного из измерений его случайное откло­нение укладывается в интервал ± 0.6745 от среднего значения.

Допустимая погрешность

В документации на некоторые детали и приборы гарантиру­ется, что отклонения их основных характеристик будут нахо­диться внутри интервала, составляющего определенный про­цент от заданных значении этих величин. Эти отклонения в данном случае и называются допустимыми погрешностями.

Суммирование погрешностей

Значение величины может определяться расчетным путем по результатам нескольких измерений, каждое из которых мо­жет иметь свои собственные погрешности. Если результаты по­лучаются:

а) суммированием измерений: для получения полной погрешнос­ти складываются абсолютные погрешности каждого измерения;

б) вычитанием измерений: для получения полной погрешности складываются абсолютные погрешности каждого измерения;

в) перемножением измерений: для получения полной относи­тельной погрешности складываются относительные погреш­ности каждого измерения;

г) делением измерений: для получения полной относительной погрешности складываются относительные погрешности каждого измерения;

д) возведением в степень: для получения полной относитель­ной погрешности показатель степени умножается на относи­тельную погрешность измерения.

Вывод вышеописанных зависимостей может быть показан на примере сложения результатов измерений. Предположим, что величина X получается в результате сложения значений двух из­мерений А и В. Тогда в случае отсутствия в измерениях каких-либо погрешностей можно записать:

Х = А + В.

Однако, принимая во внимание погрешности, это выражение превратится в

XX=AA+BB.

Таким образом,

X=A+B.

При сложении результатов двух измерений их погрешности складываются.

При перемножении результатов двух измерений в случае от­сутствия погрешностей можно записать:

X=AB.

Учитывая погрешности, это выражение примет вид:

XX=(AA)(BB).

Пренебрегая малыми величинами, можно записать:

XX=ABABBA).

X=AB+BA.

Следовательно,

Относительная погрешность X равна сумме относительных погрешностей измерений.

То же самое справедливо и для процентных погрешностей.

4. ПОМЕХИ

Виды помех

Термин «помехи» чаще всего используется для обозначения нежелательных сигналов, которые могут улавливаться системой измерения и интерферировать с полезным сигналом. Существу­ют два вида помех:

1. Наводка (интерференция). Она возникает из-за влияния внешних электромагнитных полей на электрическую цепь из­мерительной системы. Например, существует интерференция между сигналами в контуре измерительной системы и распо­ложенными поблизости мощными электроприборами, осо­бенно если они включены в одну электросеть.

2. Случайный шум. Этот вид помехи возникает из-за хаотиче­ского движения электронов и других заряженных частиц в элементах и определяется основными физическими характе­ристиками компонентов данной системы.

Виды интерференции

Существуют три основных вида интерференции:

1. Обусловленная индуктивной связью. Иногда этот вид интер­ференции относят к электромагнитной или магнитной свя­зи. Изменение тока в близкорасположенных электрических цепях приводит к изменению магнитного поля в проводниках. Изменение магнитного поля индуцирует в проводниках систе­мы измерения вторичную э.д.с. — наводку.

2. Обусловленная емкостной связью. В измерительных систе­мах силовые кабели, провода заземления и проводники рас­полагаются близко друг от друга и отделяются только возду­хом и диэлектрическими покрытиями. Поэтому между сило­выми кабелями и проводниками и между проводниками и за­землением может появиться некоторая электрическая ем­кость. Это и есть емкостная связь между проводниками из­мерительной системы и остальной частью системы, которая и приводит к возникновению интерференции сигналов.

3. Обусловленная плохим заземлением системы. В измери­тельной системе могут возникнуть проблемы с помехами, если в ней существует несколько точек заземления, так как между ними может появиться некоторая разность потенци­алов. Если это произойдет, то в цепи заземление - измери­тельный контур системы может возникнуть интерференционный электрический ток, который и является причиной помехи.

Уменьшение интерференции

Существуют следующие способы уменьшения интерферен­ции (наводки):

1. Использование витых пар проводов. Элементы измеритель­ной системы соединяются витыми парами проводов (Рис. 6.1). Изменение магнитного поля будет индуцировать вторичную э.д.с. одного направления и величины в обоих проводах каж­дой части витой пары. Но если в одном проводе пары наведен­ная э.д.с. совпадает с направлением э.д.с. основного тока, то в смежном проводе пары ее направление противоположно ос­новной э.д.с. Таким образом, результат влияния наведенных э.д.с. станет нулевым.

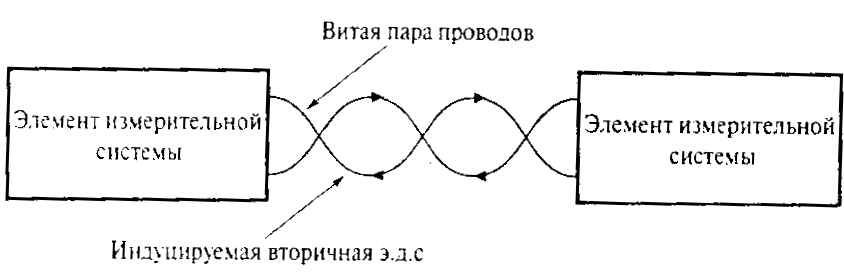
Рис. 6.1. Уменьшение интерференции при помощи витых пар проводов

2. Электростатическое экранирование. Идеальный способ предотвращения возникновения емкостной связи — это защи­та электрических контуров датчика и всей измерительной си­стемы заземленным металлическим экраном. Но при этом мо­гут возникнуть проблемы с контактным заземлением, напри­мер в случае, если датчик и устройство отображения имеют разные точки заземления. Коаксиальный кабель экранирует провода, соединяющие элементы измерительной системы между собой, однако при этом кабель должен иметь заземле­ние только на одном конце для того, чтобы избежать много­контактного заземления.

3. Использование единственной точки заземления. Наличие единственной точки заземления предотвратит случаи мно­гоконтактного заземления.

4. Использование дифференциальных усилителей. Дифферен­циальный усилитель используется для усиления разности двух сигналов. Следовательно, если оба сигнала содержат один и тот же интерференционный шум, выходной сигнал усилителя уже не будет его содержать, так как он не будет усиливаться.

5. Использование фильтров. Селективный фильтр пропускает полезный сигнал измерительной системы, а интерференци­онные шумы подавляет.

Дополнительная литература: Putten A. F. P. van (1988), Elec­tronic Measurement System, Prentice Hall.

Взаимные помехи

В некоторых измерительных системах выходы нескольких датчиков могут быть подсоединены при помощи многожильных кабелей или ленточных проводов. Термин «взаимные помехи» используется для описания интерференции, появляющейся меж­ду сигналами, передающимися по таким проводам. Этот вид ин­терференции является комбинацией емкостных и индуктивных связей. Взаимные помехи могут быть уменьшены увеличением расстояния между проводами, экранированием наиболее излуча­ющих цепей, а в случае ленточных проводов — использованием чередования измерительных проводов и проводов заземления.

Случайные шумовые помехи

Случайные помехи могут быть следующих типов:

1. Тепловой шум (иногда его называют шумом Джонсона). Этот шум генерируется хаотическими движениями электро­нов и других заряженных частиц в резисторах и полупровод­никах. Такой шум имеет непрерывный и равномерный спектр во всем частотном диапазоне, поэтому его также называют белым шумом. Эквивалентная (среднеквадратическая) э.д.с. для этого вида шума в голосе частот от f₁, до f₂; равна:

,

где k — постоянная Больцмана, R — сопротивление, Т— аб­солютная температура. Таким образом, широкополосные усилители производят больше белого шума, чем узкополос­ные. Большое сопротивление и высокая температура также будут причиной увеличения шума.

2. Дробовой шум. Этот шум возникает из-за случайных флук­туации скорости диффузии заряженных частиц через потен­циальные барьеры, такие как p-n-переходы. Эквивалентная э.д.с. для этого вида шума в полосе частот от f₁, до f₂ при аб­солютной температуре T равна:

,

где k — постоянная Больцмана, r_d — дифференциальное со­противление диода, равное kT/qI, здесь q — заряд электрона, а I — постоянный ток в переходе.

3. Фликкер-шум (шум мерцаний). Этот вид шума возникает из-за движения потока заряженных частиц в неоднородной сре­де. Пример такого шума — шум, возникающий в композитных углеродистых резисторах. Эквивалентная э.д.с. для этого вида шума приблизительно обратно пропорциональна частоте.

4. Шум из-за дребезга контактов. Шум может появиться из-за плохого соединения. Причиной этого может быть либо грязь на контактах, либо плохая пайка.

Дополнительная литература: Putten A. F. P. van (1988), Elec­tronic Measurement System, Prentice Hall.

Подавление случайных шумовых помех

Термин «нормальный шум» используется для описания всех шумов, возникающих внутри источника сигналов. Для измери­тельной системы этот шум неотличим от фактического измеряе­мого сигнала. Способность системы подавлять такой шум харак­теризуется коэффициентом подавления нормального шума (КПНШ). Он может определяться в децибелах в виде:

,

где V_n — пиковое значение нормального шума, V_e — пиковое значение погрешности от этого шума при измерениях на опреде­ленной частоте.

Термин «синфазный шум» используется для описания шума, возникающего между выводом заземления и низкопотенциаль­ным выводом измерительной системы. Способность измери­тельной системы подавлять такие шумы и не допускать возник­новения погрешностей в показаниях прибора называется коэф­фициентом подавления синфазного шума (КПСШ). Он опре­деляется в децибелах в виде:

,

где V_cm — максимальное значение синфазного шума, V_e — пико­вое значение погрешности от этого шума при измерениях на оп­ределенной частоте.

Отношение сигнал/шум

Отношение сигнал/шум (S/N) — это отношение мощности сигнала к мощности шума.

.

Оно обычно выражается в децибелах, следовательно:

.