В результат измерения вводится первая поправка (первая итерация):

y₃=K_сиx+D+K_сиdx-Dy₁=K_сиx-d(D+ K_сиdx). (8.14)

Далее повторяется итерационная процедура.

Результат преобразования y₃

. (8.15)

Результат измерения x_оп2:

. (8.16)

Вычисление поправки Dy₂ и запоминание:

. (8.17)

Новое измерение x и внесение второй поправки (вторая итерация):

. (8.18)

Поскольку d<1, то процесс итерации сходится. После n итераций получим результат:

. (8.19)

При d<1 , следовательно,

.

Практически полной коррекции погрешности измерения добиться невозможно, так как будут оказывать влияние неточности средств, задействованных в итерационной процедуре.

Основным достоинством итерационных методов является корректирование общей погрешности СИ независимо от вызвавших ее причин.

Недостатки: ограниченная область применения из-за необходимости использования достаточно точного обратного преобразователя; необходимость оценки и учета погрешности дискретизации, связанной с периодическим отключением измеряемой величины.

При реализации итерационных методов с пространственным разделением каналов отключение измеряемой величины не требуется. На рис. 8.5 представлена структурная схема такой системы итеративной коррекции. В состав системы входит несколько одинаковых прямых (ПП) и обратных образцовых (ОП) преобразователей.

Преобразования, реализуемые системой:

и т.д.

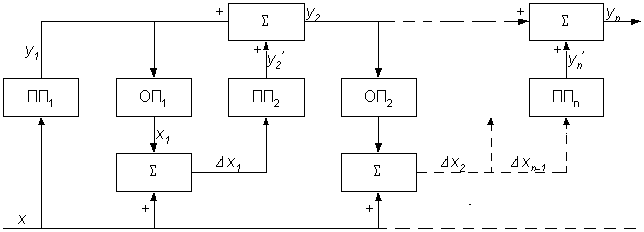
Рис. 8.5. Структурная схема реализации метода итеративной коррекции

погрешностей с пространственным разделением каналов

 

Поскольку d<<1, то y_n»K_ппx+D. Это означает, что мультипликативная погрешность скорректирована полностью, но остается аддитивная погрешность последнего преобразователя.

Методы образцовых мер (сигналов) основаны на определении в процессе цикла измерений реальных значений параметров функции преобразования средства измерений путем отключения от входа СИ измеряемой величины и подключения образцовых мер.

Метод предполагает, что функция преобразования средства измерений с достаточной точностью описывается полиномом порядка n-1.

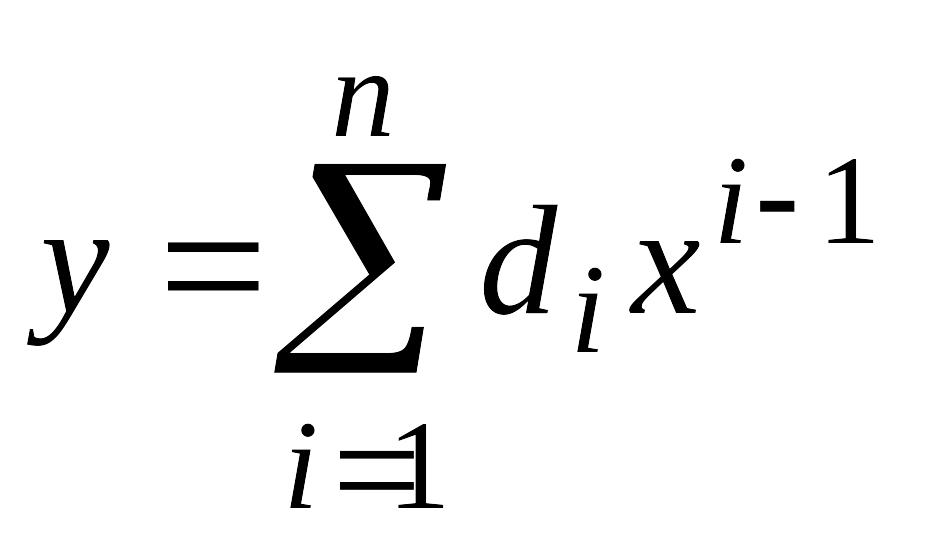, (8.20)

где d_i – коэффициенты функции преобразования средства измерений.

Структурная схема измерительной системы, реализующей данный метод, показана на рис. 8.6.

 

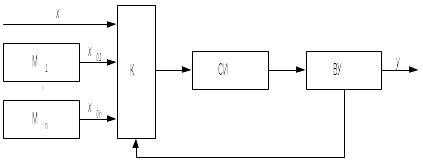
Рис. 8.6. Структурная схема измерительной системы

с образцовыми сигналами

 

В состав системы кроме средства измерений си входит набор мер м1,…,Мn, коммутатор к, вычислительное устройство ву.

Процедура измерения состоит из n+1 такта. В первом такте коммутатор подключает к входу СИ измеряемую величину x. Во втором и последующих n тактах коммутатор последовательно подключает к входу СИ меры М₁, М₂,…,М_n­ с выходными образцовыми сигналами x₀₁, x₀₂,…,x_0n­. Полученные результаты измерений y₀₁, y₀₂,…,y_0n поступают в ВУ, в памяти которого записана статическая характеристика СИ, в виде (8.20). Таким образом, формируется система из n уравнений:

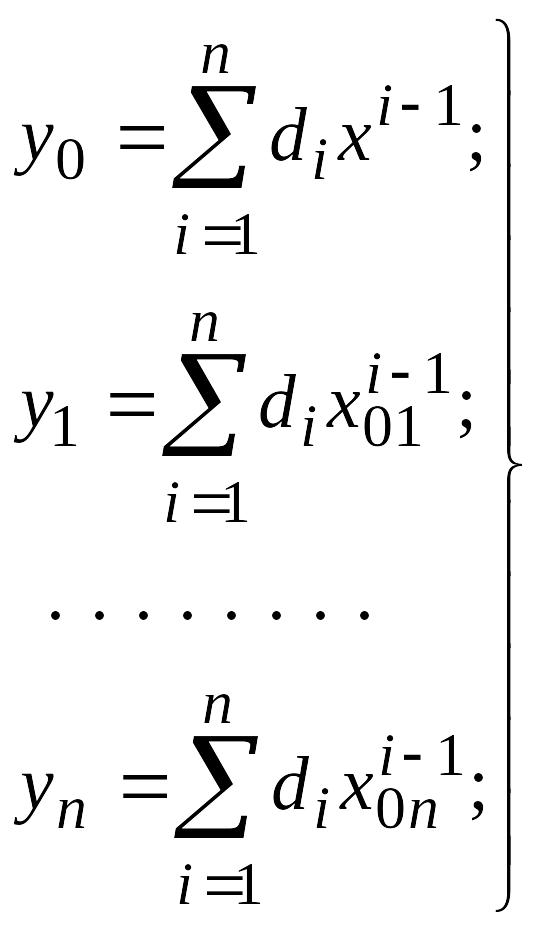(8.21)

 

Решая (8.21), ВУ вычисляет параметры d₁, d₂,…,d_i , значения которых подставляются в первое уравнение.

Если СИ имеет линейную функцию преобразования, то система (8.21) будет состоять из трех уравнений:

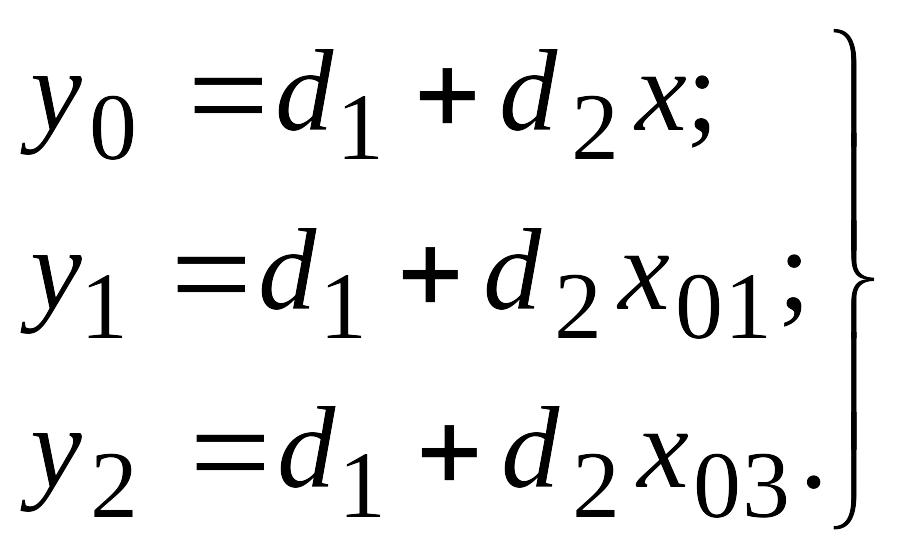(8.22)

Решение системы (8.22) относительно x имеет вид

. (8.23)

Как видно из (8.23), вычисленное значение x и, следовательно, результат измерения не зависят от изменений функции преобразования средства измерений, связанных с изменением коэффициентов d_i под действием влияющих факторов.

Метод уменьшает как мультипликативную, так и аддитивную составляющие погрешности измерения. Метод применим и при нелинейной функции преобразования средства измерений. В этом случае прибегают к кусочно-линейной ее аппроксимации, при которой связь между выходной и входной величинами выражается в виде

(8.24)

где m – число линейных участков, которыми может быть с требуемой точностью аппроксимирована функция преобразования средства измерений.

Вычисление x производится также по результатам трех измерений:

, (8.25)

где x_0i, x_0i+1 – образцовые сигналы соответствующих мер, выбираемые в зависимости от первого измерения так, как это показано на рис.8.7.

Р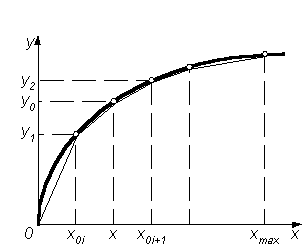 ис. 8.7. Выбор образцовых сигналов

при кусочно-линейной аппроксимации

нелинейной функции преобразования СИ

К недостаткам метода образцовых мер следует отнести частые переключения входных сигналов при измерениях, а также необходимость использования большого количества образцовых мер.

Тестовые методы [23] основаны на получении в процессе измерительного цикла информации не только об измеряемой величине, но и о параметрах функции преобразования средства измерений в момент измерения.

Тестовые методы так же, как и метод образцовых сигналов, предполагает, что функция преобразования описывается полиномом порядка n-1 (8.20), содержащим n параметров d_i. Общим между этими методами является то, что цикл измерений состоит из n+1 тактов и в первом такте измеряется величина x.

В отличие от метода образцовых сигналов, при последующих тактах измерения используются тесты A₁(x), A₂(x),…,A_n(x), каждый из которых является некоторой функцией измеряемой величины x.

Чаще всего используются аддитивные тесты в виде суммы A_j(x)=x+q_j, где q_j – образцовая величина, физически однородная с измеряемой, совместно с мультипликативными тестами, формируемыми в виде произведения A_j(x)=K_jx, где K_j – известный коэффициент передачи. Тесты третьего вида – функциональные – используется сравнительно редко.

Искомые значения x и значения параметров d₁, d₂,…,d_n получаются решением системы уравнений:

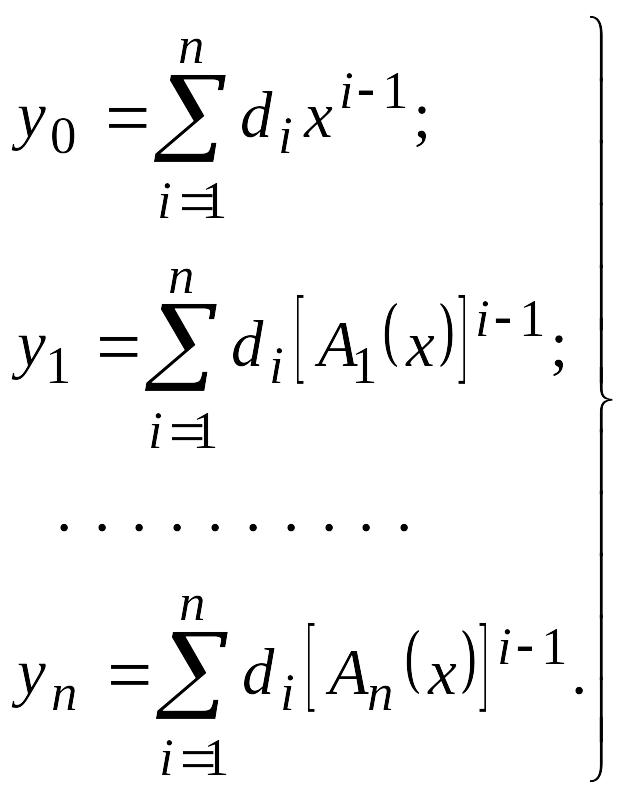(8.26)

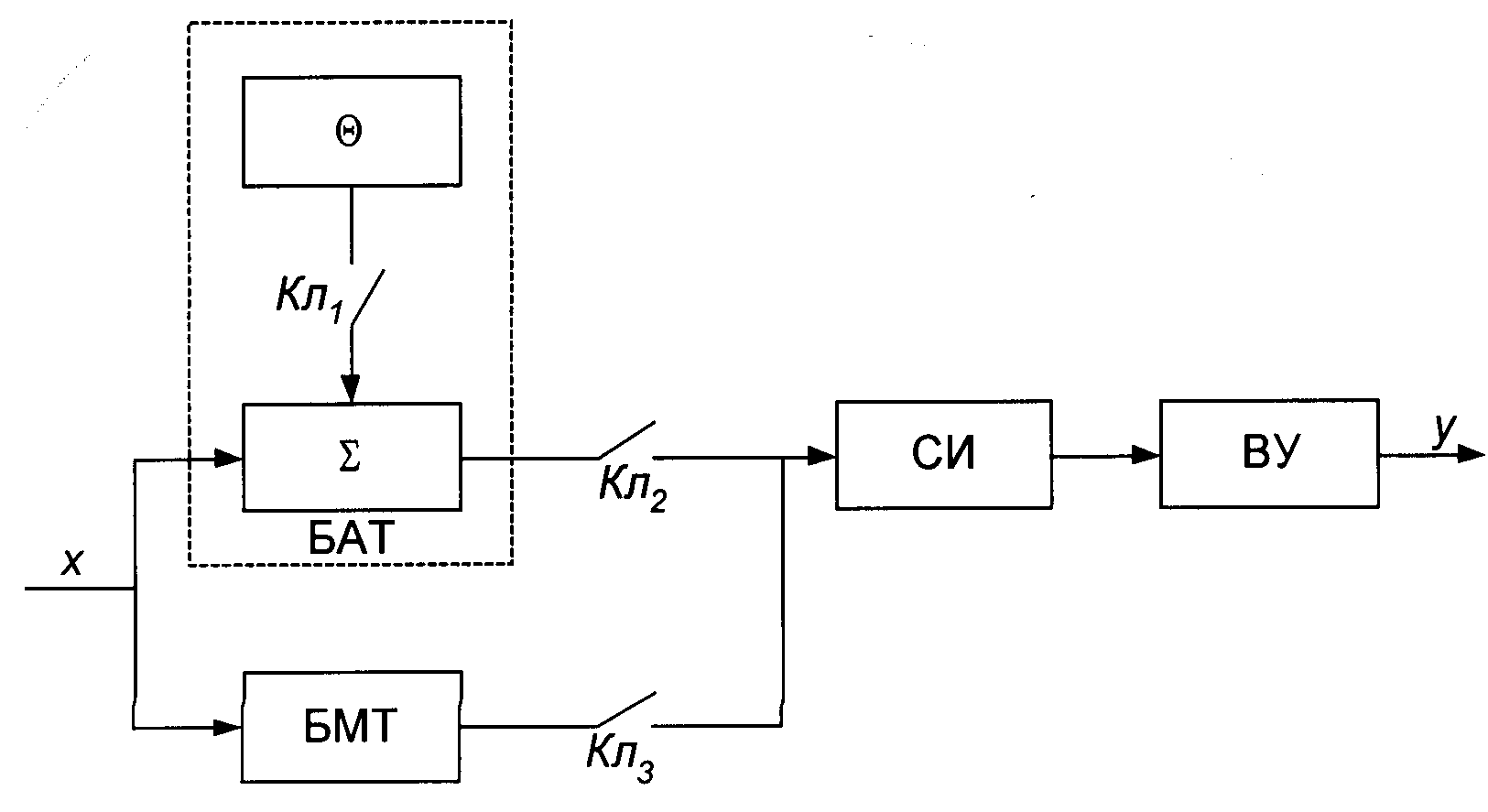
Структурная схема одного из вариантов реализации тестового метода показана на рис.8.8. В состав используемых средств помимо средства измерений и вычислительного устройства ВУ входят блоки формирования БАТ и БМТ аддитивного и мультипликативного тестов и коммутирующие ключи Кл₁, Кл₂, Кл₃, с помощью которых осуществляются такты процесса измерения. На первом такте при разомкнутых ключах Кл₁, Кл₃ и замкнутом Кл₂ на СИ подается непосредственно входная величина x. Во втором такте замыкается ключ Кл₁ и на вход СИ подается аддитивный тест x+q. В третьем такте ключ Кл₂ размыкается, а ключ Кл₃ замыкается и на вход СИ подается мультипликативный тест kx.

 

 

Рис. 8.8. Структурная схема реализации тестового метода

 

 

Рис.8.9. Функция преобразования СИ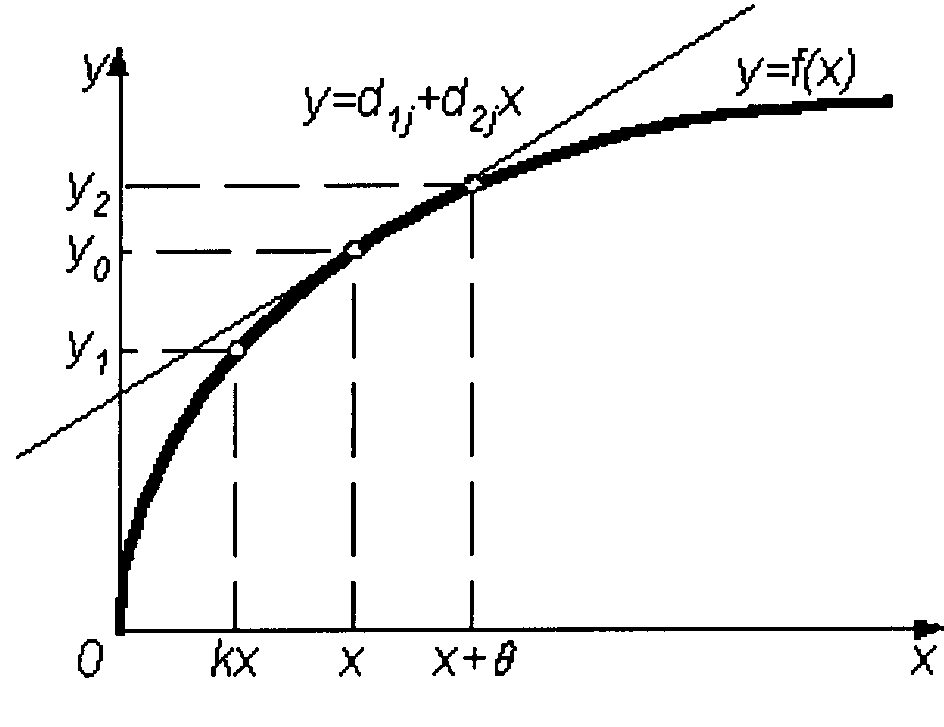

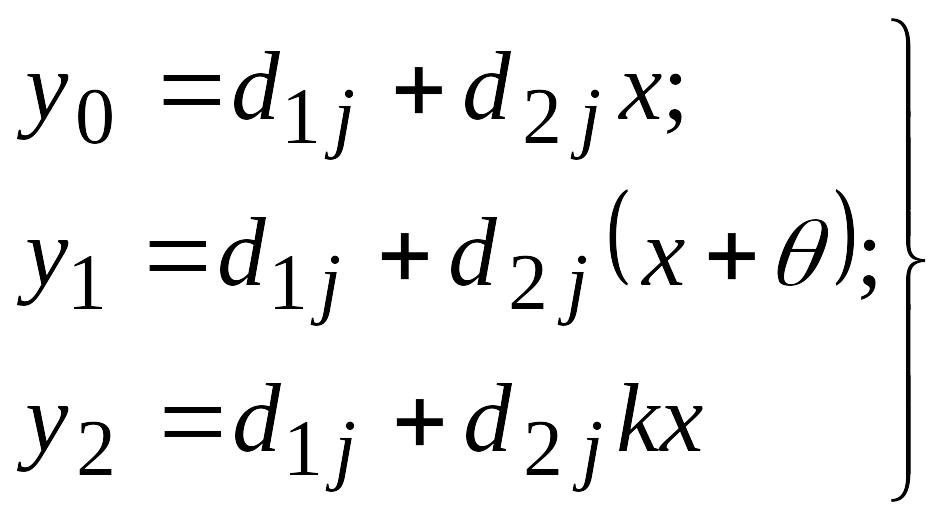Если функция преобразования СИ нелинейная (рис.8.9) и используется ее кусочно-линейная аппроксимация, то результаты тактовых измерений представляются в виде системы

(8.27)

и запоминаются вычислительным устройством. Решив эту систему относительно x по формуле

(8.28)

вычислительное устройство выдает результат измерения. Границы j -го интервала аппроксимации соответствуют значениям kx и x+q. При изменении x соответствующее смещение границ означает переход на новый интервал аппроксимации. Таким образом, для реализации метода необходимо получение точных и стабильных q и k. Технически это легче достижимо для q, чем для k.

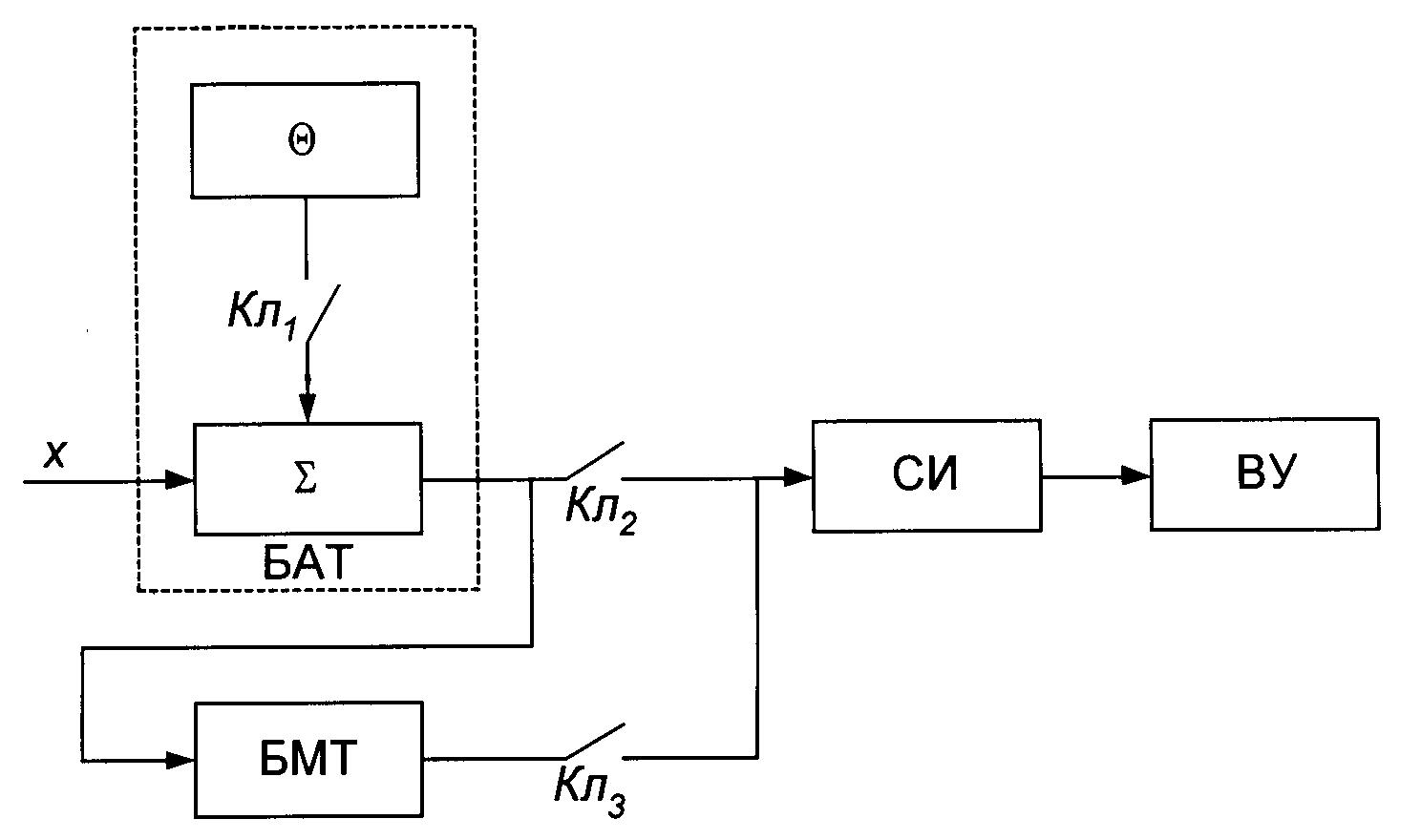
Эта проблема может быть решена некоторым изменением структуры (рис. 8.10) и алгоритма работы корректирующей системы соединением входа БМТ с выходом БАТ и введением одного дополнительного такта измерения.

Рис. 8.10. Система коррекции погрешностей тестовым методом

 

Первые три такта измерений проходят так же, как при использовании системы, изображенной на рис. 8.8. В четвертом такте ключ Кл₂ разомкнут, а ключи Кл₁ и Кл₃ замкнуты. При этом входной величиной СИ является тест k(x+q), а результат измерения

. (8.29)

Тогда в результате совместного решения (8.27) и (8.29) получается

, (8.30)

и, следовательно, коэффициент k не влияет на результат измерения.

По сравнению с методом образцовых сигналов, тестовые методы обладают существенными преимуществами. Это отсутствие необходимости в процессе измерения отключать измеряемую величину от входа СИ и использовать большое количество образцовых величин, даже при существенной нелинейности функции преобразования средства измерения.